9.2 Uniform circular motion by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
9.2 Uniform circular motion
In this section I derive a simple and very useful equation for the magnitude of the acceleration of an object undergoing constant acceleration. The law of sines is involved, so I've recapped it in figure i.
The derivation is brief, but the method requires some explanation and justification. The idea is to calculate a `Deltav` vector describing the change in the velocity vector as the object passes through an angle `theta`. We then calculate the acceleration, `a= Delta v `/`Delta t`. The astute reader will recall, however, that this equation is only valid for motion with constant acceleration. Although the magnitude of the acceleration is constant for uniform circular motion, the acceleration vector changes its direction, so it is not a constant vector, and the equation `a= Delta v `/`Delta t` does not apply. The justification for using it is that we will then examine its behavior when we make the time interval very short, which means making the angle `theta` very small. For smaller and smaller time intervals, the `Deltav"/"Deltat` expression becomes a better and better approximation, so that the final result of the derivation is exact.
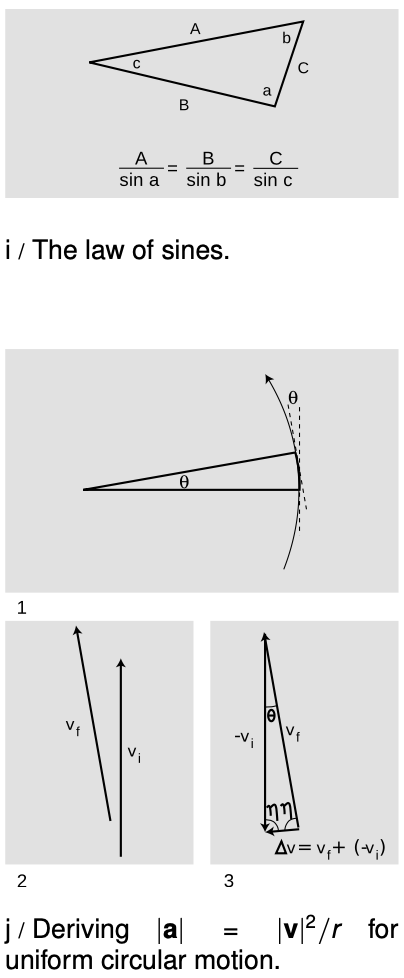
In figure j/1, the object sweeps out an angle `theta`. Its direction of motion also twists around by an angle `theta`, from the vertical dashed line to the tilted one. Figure j/2 shows the initial and final velocity vectors, which have equal magnitude, but directions differing by `theta`. In j/3, I've reassembled the vectors in the proper positions for vector subtraction. They form an isosceles triangle with interior angles `theta`, `eta`, and `eta`. (Eta, `eta`, is my favorite Greek letter.) The law of sines gives
`|Deltav|/(sintheta) =|v|/sineta.`
This tells us the magnitude of `Deltav`, which is one of the two ingredients we need for calculating the magnitude of `a= Delta v `/`Delta t`. The other ingredient is `Deltat`. The time required for the object to move through the angle `theta` is
`Deltat=("length of arc")/|v|`.
Now if we measure our angles in radians we can use the definition of radian measure, which is [Private Equation], giving `Deltat =theta r"/"|v|`. Combining this with the first expression involving `|Deltav|` gives
`|a|=|Deltav|"/"Deltat`
`=|v|^2/r*(sintheta)/theta*1/(sineta).`
When `theta` becomes very small, the small-angle approximation `sinthetaapproxtheta` applies, and also `eta` becomes close to 90°, so `sinetaapprox1`, and we have an equation for `|a|`:
`|a|=(|v|^2)/r`. [uniform circular motion]
Example 4: Force required to turn on a bike
`=>` A bicyclist is making a turn along an arc of a circle with radius 20 m, at a speed of 5 m/s. If the combined mass of the cyclist plus the bike is 60 kg, how great a static friction force must the road be able to exert on the tires?
`=>` Taking the magnitudes of both sides of Newton's second law gives
`|F|=|ma|`
|F| = m|a|
Substituting `|a|=|v|^2"/"r` gives
`|F|=m|v|^2/r`
80 N
(rounded off to one sig fig).
Example 5: Don't hug the center line on a curve!
`=>` You're driving on a mountain road with a steep drop on your right. When making a left turn, is it safer to hug the center line or to stay closer to the outside of the road?
`=>` You want whichever choice involves the least acceleration, because that will require the least force and entail the least risk of exceeding the maximum force of static friction. Assuming the curve is an arc of a circle and your speed is constant, your car is performing uniform circular motion, with `|a|=|v|^2"/"r`. The dependence on the square of the speed shows that driving slowly is the main safety measure you can take, but for any given speed you also want to have the largest possible value of `r`. Even though your instinct is to keep away from that scary precipice, you are actually less likely to skid if you keep toward the outside, because then you are describing a larger circle.
 Example 6: Acceleration related to radius and period of rotation
Example 6: Acceleration related to radius and period of rotation
`=>` How can the equation for the acceleration in uniform circular motion be rewritten in terms of the radius of the circle and the period, `T` , of the motion, i.e., the time required to go around once?
`=>` The period can be related to the speed as follows:
|v|= circumference/T.
= 2•π•r/T.
Substituting into the equation `|a|=|v|^2"/"r` gives
Example 7: A clothes dryer
`=>` My clothes dryer has a drum with an inside radius of 35 cm, and it spins at 48 revolutions per minute. What is the acceleration of the clothes inside?
`=>` We can solve this by finding the period and plugging in to the result of the previous example. If it makes 48 revolutions in one minute, then the period is 1/48 of a minute, or 1.25 s. To get an acceleration in mks units, we must convert the radius to 0.35 m. Plugging in, the result is 8.8 `m"/"s^2`.
Example 8: More about clothes dryers!
`=>` In a discussion question in the previous section, we made the assumption that the clothes remain against the inside of the drum as they go over the top. In light of the previous example, is this a correct assumption?
`=>` No. We know that there must be some minimum speed at which the motor can run that will result in the clothes just barely staying against the inside of the drum as they go over the top. If the clothes dryer ran at just this minimum speed, then there would be no normal force on the clothes at the top: they would be on the verge of losing contact. The only force acting on them at the top would be the force of gravity, which would give them an acceleration of . The actual dryer must be running slower than this minimum speed, because it produces an acceleration of only `8.8 m"/"s^2`. My theory is that this is done intentionally, to make the clothes mix and tumble.
`=>` Solved problem: The tilt-a-whirl — problem 6"
`=>` Solved problem: An off-ramp — problem 7
Discussion Questions
A A certain amount of force is needed to provide the acceleration of circular motion. What if we are exerting a force perpendicular to the direction of motion in an attempt to make an object trace a circle of radius `r`, but the force isn't as big as `m|v|^2"/"r`?
B Suppose a rotating space station, as in figure l on page 249, is built. It gives its occupants the illusion of ordinary gravity. What happens when a person in the station lets go of a ball? What happens when she throws a ball straight “up” in the air (i.e., towards the center)?
 l / Discussion question B. An artist's conception of a rotating space colony in the form of a giant wheel. A person living in this noninertial frame of reference has an illusion of a force pulling her outward, toward the deck, for the same reason that a person in the pickup truck has the illusion of a force pulling the bowling ball. By adjusting the speed of rotation, the designers can make an acceleration `|v|^2"/"r` equal to the usual acceleration of gravity on earth. On earth, your acceleration standing on the ground is zero, and a falling rock heads for your feet with an acceleration of `9.8 m"/"s^2`. A person standing on the deck of the space colony has an upward acceleration of `9.8 m"/"s^2`, and when she lets go of a rock, her feet head up at the non-accelerating rock. To her, it seems the same as true gravity.
l / Discussion question B. An artist's conception of a rotating space colony in the form of a giant wheel. A person living in this noninertial frame of reference has an illusion of a force pulling her outward, toward the deck, for the same reason that a person in the pickup truck has the illusion of a force pulling the bowling ball. By adjusting the speed of rotation, the designers can make an acceleration `|v|^2"/"r` equal to the usual acceleration of gravity on earth. On earth, your acceleration standing on the ground is zero, and a falling rock heads for your feet with an acceleration of `9.8 m"/"s^2`. A person standing on the deck of the space colony has an upward acceleration of `9.8 m"/"s^2`, and when she lets go of a rock, her feet head up at the non-accelerating rock. To her, it seems the same as true gravity.
9.2 Uniform circular motion by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.