8.3 The force vector and simple machines by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
8.3 The force vector and simple machines
Force is relatively easy to intuit as a vector. The force vector points in the direction in which it is trying to accelerate the object it is acting on.
Since force vectors are so much easier to visualize than acceleration vectors, it is often helpful to first find the direction of the (total) force vector acting on an object, and then use that to find the direction of the acceleration vector. Newton's second law tells us that the two must be in the same direction.
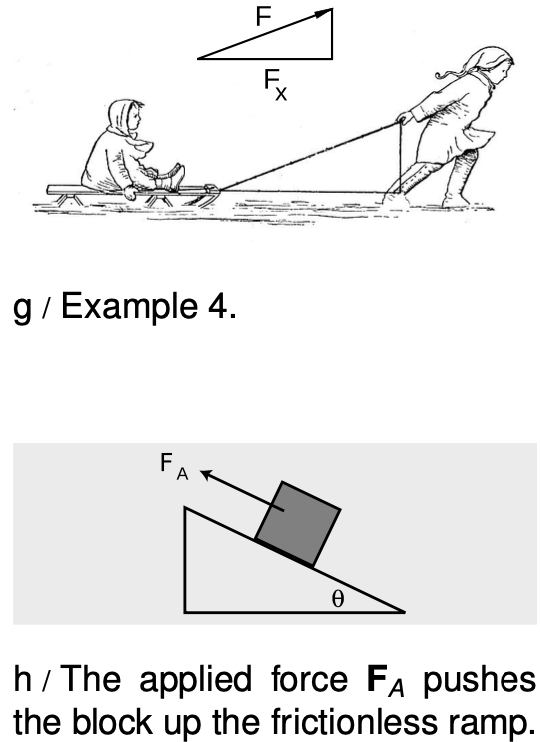 Example 4: A component of a force vector
Example 4: A component of a force vector
Figure g, redrawn from a classic 1920 textbook, shows a boy pulling another child on a sled. His force has both a horizontal component and a vertical one, but only the horizontal one accelerates the sled. (The vertical component just partially cancels the force of gravity, causing a decrease in the normal force between the runners and the snow.)
There are two triangles in the figure. One triangle's hypotenuse is the rope, and the other's is the magnitude of the force. These triangles are similar, so their internal angles are all the same, but they are not the same triangle. One is a distance triangle, with sides measured in meters, the other a force triangle, with sides in newtons. In both cases, the horizontal leg is 93% as long as the hypotenuse. It does not make sense, however, to compare the sizes of the triangles `-` the force triangle is not smaller in any meaningful sense.
Example 5: Pushing a block up a ramp
`=>` Figure h shows a block being pushed up a frictionless ramp at constant speed by an externally applied force  `F_A`. How much force is required, in terms of the block's mass, `m`, and the angle of the ramp, `theta`.
`F_A`. How much force is required, in terms of the block's mass, `m`, and the angle of the ramp, `theta`.
`=>` We analyze the forces on the block and introduce notation for the other forces besides `F_A`:

Because the block is being pushed up at constant speed, it has zero acceleration, and the total force on it must be zero. From figure i, we find
Since the sine is always less than one, the applied force is always less than `m_g`, i.e., pushing the block up the ramp is easier than lifting it straight up. This is presumably the principle on which the pyramids were constructed: the ancient Egyptians would have had a hard time applying the forces of enough slaves to equal the full weight of the huge blocks of stone.
Essentially the same analysis applies to several other simple machines, such as the wedge and the screw.
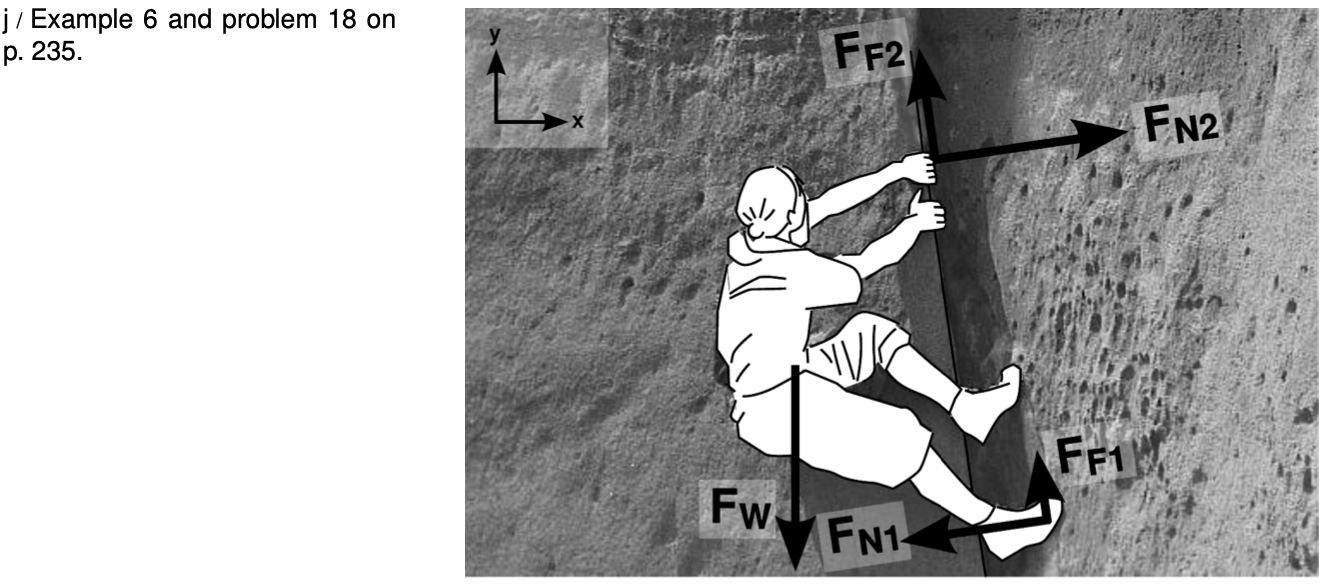
Example 6: A layback
The figure shows a rock climber using a technique called a layback. He can make the normal forces `F_(N1)` and `F_(N2)` large, which has the side-effect of increasing the frictional forces `F_(F1)` and `F_(F2)`, so that he doesn't slip down due to the gravitational (weight) force `F_W`. The purpose of the problem is not to analyze all of this in detail, but simply to practice finding the components of the forces based on their magnitudes. To keep the notation simple, let's write `F_(N1)` for `|F_(N1)|`, etc. The crack overhangs by a small, positive angle `theta approx`9°.
In this example, we determine the `x` component of `F_(N1)`. The other nine components are left as an exercise to the reader (problem 18, p. 235).
The easiest method is the one demonstrated in example 5 on p. 207. Casting vector `F_(N1)`'s shadow on the ground, we can tell that it would point to the left, so its `x` component is negative. The only two possibilities for its `x` component are therefore `-F_(N1)costheta` or `-F_(N1)sintheta`. We expect this force to have a large`x` component and a much smaller `y`. Since `theta` is small, `costheta approx 1`, while `sintheta` is small. Therefore the `x` component must be `-F_(N1)costheta`.
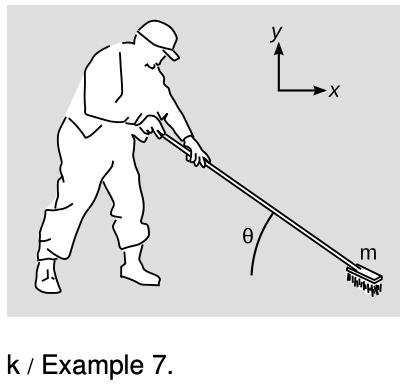 Example 7: Pushing a broom
Example 7: Pushing a broom
`=>` Figure k shows a man pushing a broom at an angle `theta` relative to the horizontal. The mass `m` of the broom is concentrated at the brush. If the magnitude of the broom's acceleration is `a`, find the force `F_H` that the man must make on the handle.
`=>` First we analyze all the forces on the brush.

Newton's second law is:
where the addition is vector addition. If we actually want to carry out the vector addition of the forces, we have to do either graphical addition (as in example 5) or analytic addition. Let's do analytic addition, which means finding all the components of the forces, adding the `x's`, and adding the `y's`.
Most of the forces have components that are trivial to express in terms of their magnitudes, the exception being `F_H`, whose components we can determine using the technique demonstrated in example 5 on p. 207 and example 6 on p. 224. Using the coordinate system shown in the figure, the results are:
`F_(Hx)= F_H•costheta` `F_(Hy)= -F_H•sintheta`
mgx = 0 mgy = -mg
FNx = 0 FNy = FN
Fkx = - Fk Fky = 0
Note that we don't yet know the magnitudes `F_H`, `F_N`, and `F_k`. That's all right. First we need to set up Newton's laws, and then we can worry about solving the equations.
Newton's second law in the `x` direction gives:
[1] `a = (F_H•costheta - F_k)/m`
The acceleration in the vertical direction is zero, so Newton's second law in the `y` direction tells us that
[2] `0 = -F_H•sintheta - m•g+F_N .`
Finally, we have the relationship between kinetic friction and the normal force,
Equations [1]-[3] are three equations, which we can use to determine the three unknowns, `F_H`, `F_N`, and `F_k`. Straightforward algebra gives
`F_H=m((a+mu_kg)/(costheta-mu_k•sintheta))`
`=>` Solved problem: A cargo plane — problem 9
`=>` Solved problem: The angle of repose — problem 11
`=>` Solved problem: A wagon — problem 10
Discussion Questions
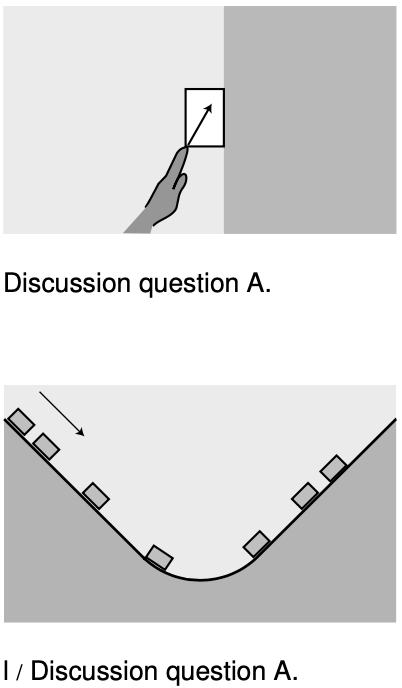
`mathbf"A"` The figure shows a block being pressed diagonally upward against a wall, causing it to slide up the wall. Analyze the forces involved, including their directions.
`mathbf"B"` The figure shows a roller coaster car rolling down and then up under the influence of gravity. Sketch the car's velocity vectors and acceleration vectors. Pick an interesting point in the motion and sketch a set of force vectors acting on the car whose vector sum could have resulted in the right acceleration vector.
8.3 The force vector and simple machines by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
 [3]
[3]