4.2 Newton's first law by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
4.2 Newton's first law

In other words, an object initially at rest is predicted to remain at rest if the total force acting on it is zero, and an object in motion remains in motion with the same velocity in the same direction. The converse of Newton's first law is also true: if we observe an object moving with constant velocity along a straight line, then the total force on it must be zero.
In a future physics course or in another textbook, you may encounter the term “net force,” which is simply a synonym for total force.
What happens if the total force on an object is not zero? It accelerates. Numerical prediction of the resulting acceleration is the topic of Newton's second law, which we'll discuss in the following section.
This is the first of Newton's three laws of motion. It is not important to memorize which of Newton's three laws are numbers one, two, and three. If a future physics teacher asks you something like, “Which of Newton's laws are you thinking of?,” a perfectly acceptable answer is “The one about constant velocity when there's zero total force.” The concepts are more important than any specific formulation of them. Newton wrote in Latin, and I am not aware of any modern textbook that uses a verbatim translation of his statement of the laws of motion. Clear writing was not in vogue in Newton's day, and he formulated his three laws in terms of a concept now called momentum, only later relating it to the concept of force. Nearly all modern texts, including this one, start with force and do momentum later.
Example 1: An elevator
`=>` An elevator has a weight of 5000 N. Compare the forces that the cable must exert to raise it at constant velocity, lower it at constant velocity, and just keep it hanging.
`=>` In all three cases the cable must pull up with a force of exactly 5000 N. Most people think you'd need at least a little more than 5000 N to make it go up, and a little less than 5000 N to let it down, but that's incorrect. Extra force from the cable is only necessary for speeding the car up when it starts going up or slowing it down when it finishes going down. Decreased force is needed to speed the car up when it gets going down and to slow it down when it finishes going up. But when the elevator is cruising at constant velocity, Newton's first law says that you just need to cancel the force of the earth's gravity.
To many students, the statement in the example that the cable's upward force “cancels” the earth's downward gravitational force implies that there has been a contest, and the cable's force has won, vanquishing the earth's gravitational force and making it disappear. That is incorrect. Both forces continue to exist, but because they add up numerically to zero, the elevator has no center-of-mass acceleration. We know that both forces continue to exist because they both have side-effects other than their effects on the car's center-of-mass motion. The force acting between the cable and the car continues to produce tension in the cable and keep the cable taut. The earth's gravitational force continues to keep the passengers (whom we are considering as part of the elevator-object) stuck to the floor and to produce internal stresses in the walls of the car, which must hold up the floor.
Example 2: Terminal velocity for falling objects
`=>` An object like a feather that is not dense or streamlined does not fall with constant acceleration, because air resistance is nonnegligible. In fact, its acceleration tapers off to nearly zero within a fraction of a second, and the feather finishes dropping at constant speed (known as its terminal velocity). Why does this happen?
`=>` Newton's first law tells us that the total force on the feather must have been reduced to nearly zero after a short time. There are two forces acting on the feather: a downward gravitational force from the planet earth, and an upward frictional force from the air. As the feather speeds up, the air friction becomes stronger and stronger, and eventually it cancels out the earth's gravitational force, so the feather just continues with constant velocity without speeding up any more.
The situation for a skydiver is exactly analogous. It's just that the skydiver experiences perhaps a million times more gravitational force than the feather, and it is not until she is falling very fast that the force of air friction becomes as strong as the gravitational force. It takes her several seconds to reach terminal velocity, which is on the order of a hundred miles per hour.
More general combinations of forces
Later in the book we'll deal with the most general case of many forces acting on an object at any angles, using the mathematical technique of vector addition, but the following slight generalization of Newton's first law allows us to analyze a great many cases of interest:
Suppose that an object has two sets of forces acting on it, one set along the line of the object's initial motion and another set perpendicular to the first set. If both sets of forces cancel, then the object's center of mass continues in the same state of motion.
Example 3: A passenger riding the subway
`=>` Describe the forces acting on a person standing in a subway train that is cruising at constant velocity.
`=>` No force is necessary to keep the person moving relative to the ground. He will not be swept to the back of the train if the floor is slippery. There are two vertical forces on him, the earth's downward gravitational force and the floor's upward force, which cancel. There are no horizontal forces on him at all, so of course the total horizontal force is zero.
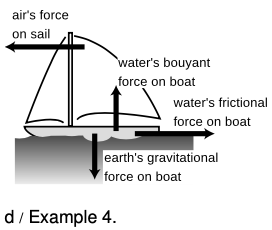 Example 4: Forces on a sailboat
Example 4: Forces on a sailboat
`=>` If a sailboat is cruising at constant velocity with the wind coming from directly behind it, what must be true about the forces acting on it?
`=>` The forces acting on the boat must be canceling each other out. The boat is not sinking or leaping into the air, so evidently the vertical forces are canceling out. The vertical forces are the downward gravitational force exerted by the planet earth and an upward force from the water.
The air is making a forward force on the sail, and if the boat is not accelerating horizontally then the water's backward frictional force must be canceling it out.
Contrary to Aristotle, more force is not needed in order to maintain a higher speed. Zero total force is always needed to maintain constant velocity. Consider the following made-up numbers:
|
|
boat moving at a low, constant velocity |
boat moving at a high, constant velocity |
| forward force of the wind on the sail … |
10,000 N |
20,000 N |
| backward force of the water on the hull … |
- 10,000 N |
- 20,000 N |
| total force on the boat … |
0 N |
0 N |
The faster boat still has zero total force on it. The forward force on it is greater, and the backward force smaller (more negative), but that's irrelevant because Newton's first law has to do with the total force, not the individual forces.
This example is quite analogous to the one about terminal velocity of falling objects, since there is a frictional force that increases with speed. After casting off from the dock and raising the sail, the boat will accelerate briefly, and then reach its terminal velocity, at which the water's frictional force has become as great as the wind's force on the sail.
Example 5: A car crash
`=>` If you drive your car into a brick wall, what is the mysterious force that slams your face into the steering wheel?
`=>` Your surgeon has taken physics, so she is not going to believe your claim that a mysterious force is to blame. She knows that your face was just following Newton's first law. Immediately after your car hit the wall, the only forces acting on your head were the same canceling-out forces that had existed previously: the earth's downward gravitational force and the upward force from your neck. There were no forward or backward forces on your head, but the car did experience a backward force from the wall, so the car slowed down and your face caught up.
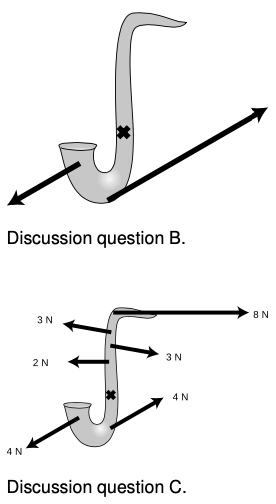 Discussion Questions
Discussion Questions
A Newton said that objects continue moving if no forces are acting on them, but his predecessor Aristotle said that a force was necessary to keep an object moving. Why does Aristotle's theory seem more plausible, even though we now believe it to be wrong? What insight was Aristotle missing about the reason why things seem to slow down naturally? Give an example.
B In the figure what would have to be true about the saxophone's initial motion if the forces shown were to result in continued one-dimensional motion of its center of mass?
C This figure requires an ever further generalization of the preceding discussion. After studying the forces, what does your physical intuition tell you will happen? Can you state in words how to generalize the conditions for one-dimensional motion to include situations like this one?
4.2 Newton's first law by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.