3.2 Acceleration by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
3.2 Acceleration
Definition of acceleration for linear v - t graphs
Galileo's experiment with dropping heavy and light objects from a tower showed that all falling objects have the same motion, and his inclined-plane experiments showed that the motion was described by `v=at+v_o`. The initial velocity `v_o` depends on whether you drop the object from rest or throw it down, but even if you throw it down, you cannot change the slope, a, of the v - t graph.
 Since these experiments show that all falling objects have linear v-t graphs with the same slope, the slope of such a graph is apparently an important and useful quantity. We use the word acceleration, and the symbol `a`, for the slope of such a graph. In symbols, a=`Delta v`/`Delta t`. The acceleration can be interpreted as the amount of speed gained in every second, and it has units of velocity divided by time, i.e., “meters per second per second,” or m/s/s. Continuing to treat units as if they were algebra symbols, we simplify “m/s/s” to read m/`s^2`. Acceleration can be a useful
Since these experiments show that all falling objects have linear v-t graphs with the same slope, the slope of such a graph is apparently an important and useful quantity. We use the word acceleration, and the symbol `a`, for the slope of such a graph. In symbols, a=`Delta v`/`Delta t`. The acceleration can be interpreted as the amount of speed gained in every second, and it has units of velocity divided by time, i.e., “meters per second per second,” or m/s/s. Continuing to treat units as if they were algebra symbols, we simplify “m/s/s” to read m/`s^2`. Acceleration can be a useful 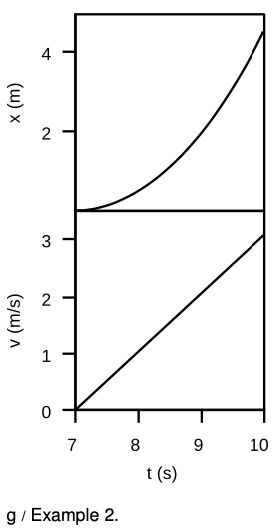 quantity for describing other types of motion besides falling, and the word and the symbol "`a`" can be used in a more general context. We reserve the more specialized symbol g for the acceleration of falling objects, which on the surface of our planet equals . Often when doing approximate calculations or merely illustrative numerical examples it is good enough to use g=10 m/`s^2`, which is off by only 2%.
quantity for describing other types of motion besides falling, and the word and the symbol "`a`" can be used in a more general context. We reserve the more specialized symbol g for the acceleration of falling objects, which on the surface of our planet equals . Often when doing approximate calculations or merely illustrative numerical examples it is good enough to use g=10 m/`s^2`, which is off by only 2%.
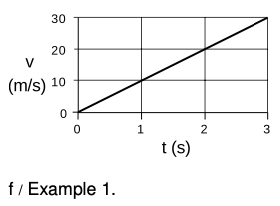
Example 1: Finding final speed, given time
⇒ A despondent physics student jumps off a bridge, and falls for three seconds before hitting the water. How fast is he going when he hits the water?
⇒ Approximating g as 10 m/`s^2`, he will gain 10 m/s of speed each second. After one second, his velocity is 10 m/s, after two seconds it is 20 m/s, and on impact, after falling for three seconds, he is moving at 30 m/s.
Example 2: Extracting acceleration from a graph
⇒ The x - t and v - t graphs show the motion of a car starting from a stop sign. What is the car's acceleration?
⇒ Acceleration is defined as the slope of the v-t graph. The graph rises by 3 m/s during a time interval of 3 s, so the acceleration is (3 m/s)/(3 s)=1 m/`s^2`.
Incorrect solution #1: The final velocity is 3 m/s, and acceleration is velocity divided by time, so the acceleration is (3 m/s)/(10 s)=0.3 m/`s^2`.
The solution is incorrect because you can't find the slope of a graph from one point. This person was just using the point at the right end of the v-t graph to try to find the slope of the curve.
Incorrect solution #2: Velocity is distance divided by time so `v`=(4.5 m)/(3 s)=1.5 m/s. Acceleration is velocity divided by time, so `a`=(1.5 m/s)/(3 s)=0.5 m/`s^2`.
The solution is incorrect because velocity is the slope of the tangent line. In a case like this where the velocity is changing, you can't just pick two points on the `x-t` graph and use them to find the velocity.
Example 3: Converting `g` to different units
⇒ What is g in units of `cm"/"s^2`?
⇒ The answer is going to be how many cm/s of speed a falling object gains in one second. If it gains 9.8 m/s in one second, then it gains 980 cm/s in one second, so g=980 cm/`s^2`. Alternatively, we can use the method of fractions that equal one:
`(9.8 m)/s^2 × (100 cm)/(1 m) =(980 cm)/s^2`
⇒ What is g in units of `"miles/hour"^2`?
`(9.8 m)/s^2 × (1 "mile")/(1600 m) × (3600 s)/(1 hour)^2 =7.9×10^4 "mile/hour"^2`
This large number can be interpreted as the speed, in miles per hour, that you would gain by falling for one hour. Note that we had to square the conversion factor of 3600 s/hour in order to cancel out the units of seconds squared in the denominator.
⇒ What is g in units of `"miles/hour/"s`?
⇒
`(9.8 m)/s^2× (1 "mile")/(1600 m)× (3600 s)/(1 hour)=22 "mile/hour/"s`
This is a figure that Americans will have an intuitive feel for. If your car has a forward acceleration equal to the acceleration of a falling object, then you will gain 22 miles per hour of speed every second. However, using mixed time units of hours and seconds like this is usually inconvenient for problem-solving. It would be like using units of foot-inches for area instead of `ft^2` or `In^2`.
The acceleration of gravity is different in different locations.
| location | latitude | elevation (m) | g(m/s2) |
| north pole | 90°N | 0 | 9.8322 |
| Reykjavik, Iceland | 64°N | 0 | 9.8225 |
| Guayaquil, Ecuador | 2°S | 0 | 9.7806 |
| Mt. Cotopaxi, Ecuador | 1°S | 5896 | 9.7624 |
| Mt. Everest | 28°N | 8848 | 9.7643 |
The main variables that relate to the value of g on Earth are latitude and elevation. Although you have not yet learned how g would be calculated based on any deeper theory of gravity, it is not too hard to guess why g depends on elevation. Gravity is an attraction between things that have mass, and the attraction gets weaker with increasing distance. As you ascend from the seaport of Guayaquil to the nearby top of Mt. Cotopaxi, you are distancing yourself from the mass of the planet. The dependence on latitude occurs because we are measuring the acceleration of gravity relative to the earth's surface, but the earth's rotation causes the earth's surface to fall out from under you.

This false-color map shows variations in the strength of the earth's gravity. Purple areas have the strongest gravity, yellow the weakest. The overall trend toward weaker gravity at the equator and stronger gravity at the poles has been artificially removed to allow the weaker local variations to show up. The map covers only the oceans because of the technique used to make it: satellites look for bulges and depressions in the surface of the ocean. A very slight bulge will occur over an undersea mountain, for instance, because the mountain's gravitational attraction pulls water toward it. The US government originally began collecting data like these for military use, to correct for the deviations in the paths of missiles. The data have recently been released for scientific and commercial use (e.g., searching for sites for off-shore oil wells).
Much more spectacular differences in the strength of gravity can be observed away from the Earth's surface:
| location | g(m/s2) |
| asteroid Vesta (surface) | 0.3 |
| Earth’s moon (surface | 1.6 |
| Mars (surface | 3.7 |
| Earth (surface) | 9.8 |
| Jupiter (cloud-tops) | 26 |
| Sun (visible surface) | 270 |
| typical neutron star (surface) | 1012 |
| black hole (center) | infinite according to some theories, on the order of 1052 according to others |
A typical neutron star is not so different in size from a large asteroid, but is orders of magnitude more massive, so the mass of a body definitely correlates with the g it creates. On the other hand, a neutron star has about the same mass as our Sun, so why is its g billions of times greater? If you had the misfortune of being on the surface of a neutron star, you'd be within a few thousand miles of all its mass, whereas on the surface of the Sun, you'd still be millions of miles from most of its mass.
Discussion Questions
⇒ What is wrong with the following definitions of `g`?
(1) “`g`" is gravity.”
(2) “`g`" is the speed of a falling object.”
(3) “`g`" is how hard gravity pulls on things.”
⇒ When advertisers specify how much acceleration a car is capable of, they do not give an acceleration as defined in physics. Instead, they usually specify how many seconds are required for the car to go from rest to 60 miles/hour. Suppose we use the notation “a" for the acceleration as defined in physics, and `a_("car ad")` for the quantity used in advertisements for cars. In the US's non-metric system of units, what would be the units of a and `a_("car ad")`? How would the use and interpretation of large and small, positive and negative values be different for a as opposed to `a_("car ad")`?
⇒ Two people stand on the edge of a cliff. As they lean over the edge, one person throws a rock down, while the other throws one straight up with an exactly opposite initial velocity. Compare the speeds of the rocks on impact at the bottom of the cliff.
3.2 Acceleration by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.