36.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
quantum number — a numerical label used to classify a quantum state
spin — the built-in angular momentum possessed by a particle even when at rest
Notation
`n` — the number of radial nodes in the wave function, including the one at r=∞
`ℏ` — `h"/"2pi`
L —the angular momentum vector of a particle, not including its spin
`ℓ` — the magnitude of the `L` vector, divided by `ℏ`
` ℓ_z` — the `z` component of the `L` vector, divided by `ℏ`; this is the standard notation in nuclear physics, but not in atomic physics
`s` — the magnitude of the spin angular momentum vector, divided by `ℏ`
`s_z` — the `z` component of the spin angular momentum vector, divided by `ℏ`; this is the standard notation in nuclear physics, but not in atomic physics
Other Notation
`m_ℓ` — a less obvious notation for `ℓ_z`, standard in atomic physics
`m_s`— a less obvious notation for `s_z`, standard in atomic physics
Summary
Hydrogen, with one proton and one electron, is the simplest atom, and more complex atoms can often be analyzed to a reasonably good approximation by assuming their electrons occupy states that have the same structure as the hydrogen atom's. The electron in a hydrogen atom exchanges very little energy or angular momentum with the proton, so its energy and angular momentum are nearly constant, and can be used to classify its states. The energy of a hydrogen state depends only on its `n` quantum number.
In quantum physics, the angular momentum of a particle moving in a plane is quantized in units of `?`. Atoms are three-dimensional, however, so the question naturally arises of how to deal with angular momentum in three dimensions. In three dimensions, angular momentum is a vector in the direction perpendicular to the plane of motion, such that the motion appears clockwise if viewed along the direction of the vector. Since angular momentum depends on both position and momentum, the Heisenberg uncertainty principle limits the accuracy with which one can know it. The most that can be known about an angular momentum vector is its magnitude and one of its three vector components, both of which are quantized in units of `?`.
In addition to the angular momentum that an electron carries by virtue of its motion through space, it possesses an intrinsic angular momentum with a magnitude of `?"/"2`. Protons and neutrons also have spins of `?"/"2`, while the photon has a spin equal to `?`.
Particles with half-integer spin obey the Pauli exclusion principle: only one such particle can exist is a given state, i.e., with a given combination of quantum numbers.
We can enumerate the lowest-energy states of hydrogen as follows:
| `n = 1`, | `ℓ=0`, | `ℓ_z=0`, | `s_z = + 1"/"2` or `-1"/"2` | two states |
| `n = 2`, | `ℓ=0`, | `ℓ_z=0`, | `s_z = + 1"/"2` or `-1"/"2` | two states |
| `n = 2`, | `ℓ=1`, | `ℓ_z=-1`, `0`, or `1`, | `s_z = + 1"/"2` or `-1"/"2` | six states |
| … | … |
The periodic table can be understood in terms of the filling of these states. The nonreactive noble gases are those atoms in which the electrons are exactly sufficient to fill all the states up to a given `n` value. The most reactive elements are those with one more electron than a noble gas element, which can release a great deal of energy by giving away their high-energy electron, and those with one electron fewer than a noble gas, which release energy by accepting an electron.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. (a) A distance scale is shown below the wave functions and probability densities illustrated in figure f on page 991. Compare this with the order-of-magnitude estimate derived in section 36.4 for the radius `r` at which the wave function begins tailing off. Was the estimate in section 36.4 on the right order of magnitude?
(b) Although we normally say the moon orbits the earth, actually they both orbit around their common center of mass, which is below the earth's surface but not at its center. The same is true of the hydrogen atom. Does the center of mass lie inside the proton or outside it?
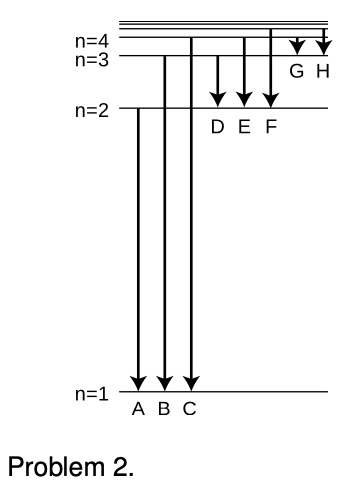 2. The figure shows eight of the possible ways in which an electron in a hydrogen atom could drop from a higher energy state to a state of lower energy, releasing the difference in energy as a photon. Of these eight transitions, only D, E, and F produce photons with wavelengths in the visible spectrum.
2. The figure shows eight of the possible ways in which an electron in a hydrogen atom could drop from a higher energy state to a state of lower energy, releasing the difference in energy as a photon. Of these eight transitions, only D, E, and F produce photons with wavelengths in the visible spectrum.
(a) Which of the visible transitions would be closest to the violet end of the spectrum, and which would be closest to the red end? Explain.
(b) In what part of the electromagnetic spectrum would the photons from transitions A, B, and C lie? What about G and H? Explain.
(c) Is there an upper limit to the wavelengths that could be emitted by a hydrogen atom going from one bound state to another bound state? Is there a lower limit? Explain.
3. Before the quantum theory, experimentalists noted that in many cases, they would find three lines in the spectrum of the same atom that satisfied the following mysterious rule: `1"/"lambda_1=1"/"lambda_2+1"/"lambda_3`. Explain why this would occur. Do not use reasoning that only works for hydrogen `-` such combinations occur in the spectra of all elements. [Hint: Restate the equation in terms of the energies of photons.]
4. Find an equation for the wavelength of the photon emitted when the electron in a hydrogen atom makes a transition from energy level `n_1` to level `n_2`. [You will need to have read optional section 36.4.] `sqrt`
5. Estimate the angular momentum of a spinning basketball, in units of `?`. Explain how this result relates to the correspondence principle.
6. Assume that the kinetic energy of an electron in the `n=1` state of a hydrogen atom is on the same order of magnitude as the absolute value of its total energy, and estimate a typical speed at which it would be moving. (It cannot really have a single, definite speed, because its kinetic and potential energy trade off at different distances from the proton, but this is just a rough estimate of a typical speed.) Based on this speed, were we justified in assuming that the electron could be described nonrelativistically?
7. The wavefunction of the electron in the ground state of a hydrogen atom, shown in the top left of figure f on p. 991, is
`Psi=pi^(-1"/"2)a^(-3"/"2)e^(-r"/"a)`
where `r` is the distance from the proton, and `a=?^2"/"(kme^2)=5.3×10^(-11) m` is a constant that sets the size of the wave. The figure doesn't show the proton; let's take the proton to be a sphere with a radius of `b=0.5` fm.
(a) Reproduce figure f in a rough sketch, and indicate, relative to the size of your sketch, some idea of how big `a` and `b` are.
(b) Calculate symbolically, without plugging in numbers, the probability that at any moment, the electron is inside the proton. [Hint: Does it matter if you plug in `r=0` or `r=b` in the equation for the wave function?] `sqrt`
(c) Calculate the probability numerically. `sqrt`
(d) Based on the equation for the wave function, is it valid to think of a hydrogen atom as having a finite size? Can aa be interpreted as the size of the atom, beyond which there is nothing? Or is there any limit on how far the electron can be from the proton?
8. Use physical reasoning to explain how the equation for the energy levels of hydrogen,
`E_n=-(mk^2e^4)/(2ℏ^2)*1/(n^2)`,
should be generalized to the case of an atom with atomic number `Z` that has had all its electrons removed except for one. `***`
9. This question requires that you read optional section 36.4. A muon is a subatomic particle that acts exactly like an electron except that its mass is 207 times greater. Muons can be created by cosmic rays, and it can happen that one of an atom's electrons is displaced by a muon, forming a muonic atom. If this happens to a hydrogen atom, the resulting system consists simply of a proton plus a muon.
(a) How would the size of a muonic hydrogen atom in its ground state compare with the size of the normal atom?
(b) If you were searching for muonic atoms in the sun or in the earth's atmosphere by spectroscopy, in what part of the electromagnetic spectrum would you expect to find the absorption lines?
10. Consider a classical model of the hydrogen atom in which the electron orbits the proton in a circle at constant speed. In this model, the electron and proton can have no intrinsic spin. Using the result of problem 14 in ch. 24, show that in this model, the atom's magnetic dipole moment `D_m` is related to its angular momentum by `D_m=(-e"/"2m)L`, regardless of the details of the orbital motion. Assume that the magnetic field is the same as would be produced by a circular current loop, even though there is really only a single charged particle. [Although the model is quantum-mechanically incorrect, the result turns out to give the correct quantum mechanical value for the contribution to the atom's dipole moment coming from the electron's orbital motion. There are other contributions, however, arising from the intrinsic spins of the electron and proton.]
11. Hydrogen is the only element whose energy levels can be expressed exactly in an equation. Calculate the ratio `lambda_E"/"lambda_F` of the wavelengths of the transitions labeled `E` and `F` in problem 2 on p. 1002. Express your answer as an exact fraction, not a decimal approximation. In an experiment in which atomic wavelengths are being measured, this ratio provides a natural, stringent check on the precision of the results. `sqrt`
Exercise 36: Quantum versus classical randomness
1. Imagine the classical version of the particle in a one-dimensional box. Suppose you insert the particle in the box and give it a known, predetermined energy, but a random initial position and a random direction of motion. You then pick a random later moment in time to see where it is. Sketch the resulting probability distribution by shading on top of a line segment. Does the probability distribution depend on energy?
2. Do similar sketches for the first few energy levels of the quantum mechanical particle in a box, and compare with `1`.
3. Do the same thing as in 1, but for a classical hydrogen atom in two dimensions, which acts just like a miniature solar system. Assume you're always starting out with the same fixed values of energy and angular momentum, but a position and direction of motion that are otherwise random. Do this for `L=0`, and compare with a real `L=0` probability distribution for the hydrogen atom.
4. Repeat `3` for a nonzero value of `L`, say `L=?`.
5. Summarize: Are the classical probability distributions accurate? What qualitative features are possessed by the classical diagrams but not by the quantum mechanical ones, or vice-versa?
36.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.