36.4 Energies of states in hydrogen by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
36.4 Energies of states in hydrogen (optional)
History
The experimental technique for measuring the energy levels of an atom accurately is spectroscopy: the study of the spectrum of light emitted (or absorbed) by the atom. Only photons with certain energies can be emitted or absorbed by a hydrogen atom, for example, since the amount of energy gained or lost by the atom must equal the difference in energy between the atom's initial and final states. Spectroscopy had become a highly developed art several decades before Einstein even proposed the photon, and the Swiss spectroscopist Johann Balmer determined in 1885 that there was a simple equation that gave all the wavelengths emitted by hydrogen. In modern terms, we think of the photon wavelengths merely as indirect evidence about the underlying energy levels of the atom, and we rework Balmer's result into an equation for these atomic energy levels:
This energy includes both the kinetic energy of the electron and the electrical energy. The zero-level of the electrical energy scale is chosen to be the energy of an electron and a proton that are infinitely far apart. With this choice, negative energies correspond to bound states and positive energies to unbound ones.
Where does the mysterious numerical factor of `2.2×10^(-18) J` come from? In 1913 the Danish theorist Niels Bohr realized that it was exactly numerically equal to a certain combination of fundamental physical constants:
`E_n=-(mk^2e^4)/(2?^2)*1/(n^2)`
where `m` is the mass of the electron, and `k` is the Coulomb force constant for electric forces.
Bohr was able to cook up a derivation of this equation based on the incomplete version of quantum physics that had been developed by that time, but his derivation is today mainly of historical interest. It assumes that the electron follows a circular path, whereas the whole concept of a path for a particle is considered meaningless in our more complete modern version of quantum physics. Although Bohr was able to produce the right equation for the energy levels, his model also gave various wrong results, such as predicting that the atom would be flat, and that the ground state would have `?=1` rather than the correct `?=0`.
Approximate treatment
A full and correct treatment is impossible at the mathematical level of this book, but we can provide a straightforward explanation for the form of the equation using approximate arguments.
A typical standing-wave pattern for the electron consists of a central oscillating area surrounded by a region in which the wave function tails off. As discussed in section 35.6, the oscillating type of pattern is typically encountered in the classically allowed region, while the tailing off occurs in the classically forbidden region where the electron has insufficient kinetic energy to penetrate according to classical physics. We use the symbol `r` for the radius of the spherical boundary between the classically allowed and classically forbidden regions. Classically, `r` would be the distance from the proton at which the electron would have to stop, turn around, and head back in.
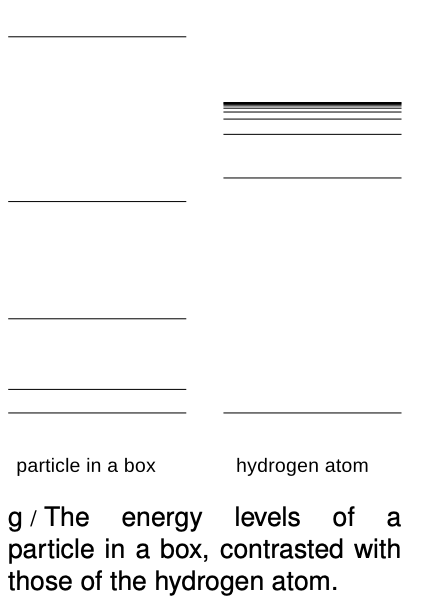If `r` had the same value for every standing-wave pattern, then we'd essentially be solving the particle-in-a-box problem in three dimensions, with the box being a spherical cavity. Consider the energy levels of the particle in a box compared to those of the hydrogen atom, g. They're qualitatively different. The energy levels of the particle in a box get farther and farther apart as we go higher in energy, and this feature doesn't even depend on the details of whether the box is two-dimensional or three-dimensional, or its exact shape. The reason for the spreading is that the box is taken to be completely impenetrable, so its size, `r`, is fixed. A wave pattern with `n` humps has a wavelength proportional to `r"/"n`, and therefore a momentum proportional to `n`, and an energy proportional to `n^2`. In the hydrogen atom, however, the force keeping the electron bound isn't an infinite force encountered when it bounces off of a wall, it's the attractive electrical force from the nucleus. If we put more energy into the electron, it's like throwing a ball upward with a higher energy `-` it will get farther out before coming back down. This means that in the hydrogen atom, we expect `r` to increase as we go to states of higher energy. This tends to keep the wavelengths of the high energy states from getting too short, reducing their kinetic energy. The closer and closer crowding of the energy levels in hydrogen also makes sense because we know that there is a certain energy that would be enough to make the electron escape completely, and therefore the sequence of bound states cannot extend above that energy.
When the electron is at the maximum classically allowed distance `r` from the proton, it has zero kinetic energy. Thus when the electron is at distance `r`, its energy is purely electrical:
`E=-(ke^2)/r`
Now comes the approximation. In reality, the electron's wavelength cannot be constant in the classically allowed region, but we pretend that it is. Since `n` is the number of nodes in the wave function, we can interpret it approximately as the number of wavelengths that fit across the diameter `2r`. We are not even attempting a derivation that would produce all the correct numerical factors like `2` and `pi` and so on, so we simply make the approximation
`lambda~r/n`
Finally we assume that the typical kinetic energy of the electron is on the same order of magnitude as the absolute value of its total energy. (This is true to within a factor of two for a typical classical system like a planet in a circular orbit around the sun.) We then have \begin{subequations} \renewcommand{\theequation}{\theparentequation}
`"absolute value of total energy"`
`=(ke^2)/r`
`~K `
`=p^2/(2m)`
`=(h"/"lambda^2)/(2m)`
`~h^2n^2"/"2mr^2`
We now solve the equation `ke^2"/"r~h^2n^2"/"2mr^2` for `r` and throw away numerical factors we can't hope to have gotten right, yielding
`r~(h^2n^2)/(mke^2).`
Plugging `n=1` into this equation gives `r=2 nm`, which is indeed on the right order of magnitude. Finally we combine equations [4] and [1] to find
`E~-(mk^2e^4)/(h^2n^2)`
which is correct except for the numerical factors we never aimed to find.
Discussion Questions
A States of hydrogen with `n` greater than about 10 are never observed in the sun. Why might this be?
B Sketch graphs of `r` and `E` versus `n` for the hydrogen, and compare with analogous graphs for the one-dimensional particle in a box.
36.4 Energies of states in hydrogen by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.