36.3 The hydrogen atom by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
36.3 The hydrogen atom
Deriving the wave functions of the states of the hydrogen atom from first principles would be mathematically too complex for this book, but it's not hard to understand the logic behind such a wave function in visual terms. Consider the wave function from the beginning of the chapter, which is reproduced below. Although the graph looks three-dimensional, it is really only a representation of the part of the wavefunction lying within a two-dimensional plane. The third (up-down) dimension of the plot represents the value of the wave function at a given point, not the third dimension of space. The plane chosen for the graph is the one perpendicular to the angular momentum vector.

 Each ring of peaks and valleys has eight wavelengths going around in a circle, so this state has `L=8?`, i.e., we label it `?=8`. The wavelength is shorter near the center, and this makes sense because when the electron is close to the nucleus it has a lower PE, a higher KE, and a higher momentum.
Each ring of peaks and valleys has eight wavelengths going around in a circle, so this state has `L=8?`, i.e., we label it `?=8`. The wavelength is shorter near the center, and this makes sense because when the electron is close to the nucleus it has a lower PE, a higher KE, and a higher momentum.
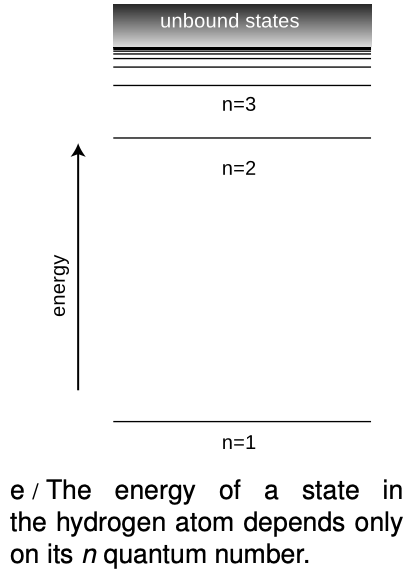
Between each ring of peaks in this wave function is a nodal circle, i.e., a circle on which the wave function is zero. The full three-dimensional wave function has nodal spheres: a series of nested spherical surfaces on which it is zero. The number of radii at which nodes occur, including `r=infty`, is called `n`, and `n` turns out to be closely related to energy. The ground state has `n=1` (a single node only at `r=infty`), and higher-energy states have higher `n` values. There is a simple equation relating `n` to energy, which we will discuss in section 36.4.
The numbers `n` and `?`, which identify the state, are called its quantum numbers. A state of a given `n` and `?` can be oriented in a variety of directions in space. We might try to indicate the orientation using the three quantum numbers `?_x=?_x/?`, `?_y=?_y/?`, and `?_z=?_z/?`. But we have already seen that it is impossible to know all three of these simultaneously. To give the most complete possible description of a state, we choose an arbitrary axis, say the `z` axis, and label the state according to `n`, `?`, and `?_z`.
Angular momentum requires motion, and motion implies kinetic energy. Thus it is not possible to have a given amount of angular momentum without having a certain amount of kinetic energy as well. Since energy relates to the `n` quantum number, this means that for a given `n` value there will be a maximum possible `?`. It turns out that this maximum value of `?` equals `n^(-1)`.
In general, we can list the possible combinations of quantum numbers as follows:
| n can equal 1, 2, 3, … |
| `?` can range from 0 to n-1, in steps of 1 |
| `?_z` can range from `-?` to `?`, in steps of 1 |
Applying these rules, we have the following list of states:
| n = 1, | `?`=0, | `?_z`=0 | one state |
| n = 2, | `?`=0, | `?_z`=0 | one state |
| n = 2, | `?`=1, | `?_z`=-1, 0, or 1 | three states |
| … | … |
self-check:
Continue the list for `n=3`.
(answer in the back of the PDF version of the book)
Figure f shows the lowest-energy states of the hydrogen atom. The left-hand column of graphs displays the wavefunctions in the `x-y` plane, and the right-hand column shows the probability distribution in a three-dimensional representation.
Discussion Questions
A The quantum number `n` is defined as the number of radii at which the wave function is zero, including `r=infty`. Relate this to the features of the figures on the facing page.
B Based on the definition of `n`, why can't there be any such thing as an `n=0` state?
C Relate the features of the wave function plots in figure f to the corresponding features of the probability distribution pictures.
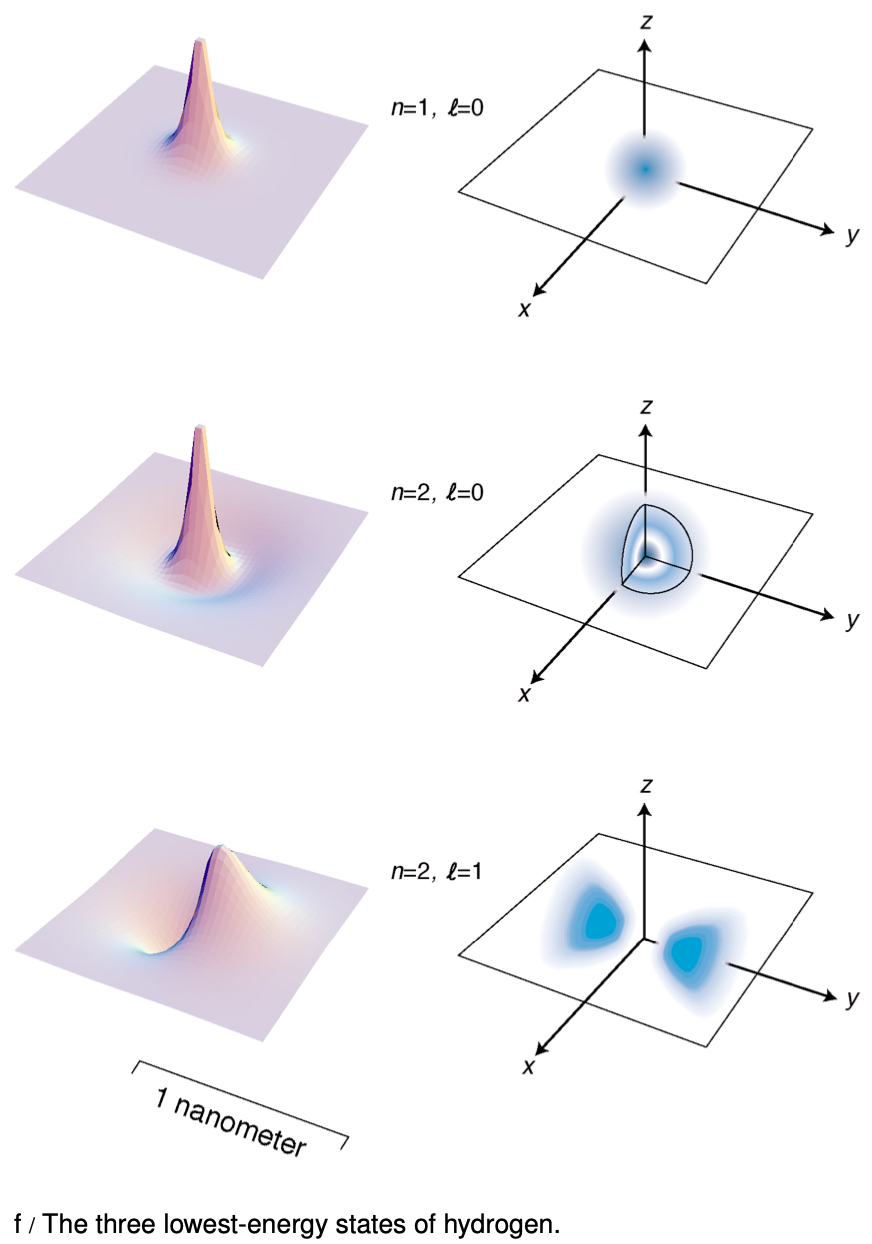
D How can you tell from the wave function plots in figure f which ones have which angular momenta?
E Criticize the following incorrect statement: “The `?=8` wave function in figure d has a shorter wavelength in the center because in the center the electron is in a higher energy level.”
F Discuss the implications of the fact that the probability cloud in of the `n=2`, `?=1` state is split into two parts.
36.3 The hydrogen atom by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.