36.1 Classifying states by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
36.1 Classifying states
We'll focus our attention first on the simplest atom, hydrogen, with one proton and one electron. We know in advance a little of what we should expect for the structure of this atom. Since the electron is bound to the proton by electrical forces, it should display a set of discrete energy states, each corresponding to a certain standing wave pattern. We need to understand what states there are and what their properties are.
What properties should we use to classify the states? The most sensible approach is to used conserved quantities. Energy is one conserved quantity, and we already know to expect each state to have a specific energy. It turns out, however, that energy alone is not sufficient. Different standing wave patterns of the atom can have the same energy.
Momentum is also a conserved quantity, but it is not particularly appropriate for classifying the states of the electron in a hydrogen atom. The reason is that the force between the electron and the proton results in the continual exchange of momentum between them. (Why wasn't this a problem for energy as well? Kinetic energy and momentum are related by `KE=p^2"/"(2m)`, so the much more massive proton never has very much kinetic energy. We are making an approximation by assuming all the kinetic energy is in the electron, but it is quite a good approximation.)
 Angular momentum does help with classification. There is no transfer of angular momentum between the proton and the electron, since the force between them is a center-to-center force, producing no torque.
Angular momentum does help with classification. There is no transfer of angular momentum between the proton and the electron, since the force between them is a center-to-center force, producing no torque.
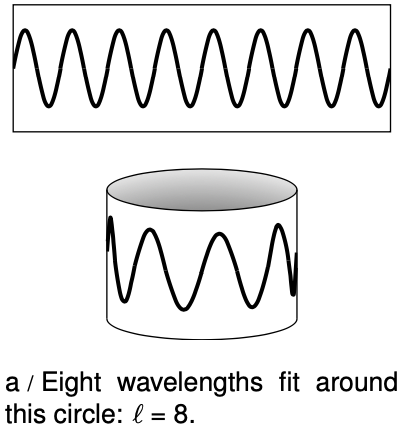
Like energy, angular momentum is quantized in quantum physics. As an example, consider a quantum wave-particle confined to a circle, like a wave in a circular moat surrounding a castle. A sine wave in such a “quantum moat” cannot have any old wavelength, because an integer number of wavelengths must fit around the circumference, `C`, of the moat. The larger this integer is, the shorter the wavelength, and a shorter wavelength relates to greater momentum and angular momentum. Since this integer is related to angular momentum, we use the symbol `?` for it:
The angular momentum is
Here, `r=C/(2pi)`, and `p=h/lambda``=(hl)/C`, so
`L=C/(2pi)*(hl)/C`
In the example of the quantum moat, angular momentum is quantized in units of `h"/"2pi`, and this turns out to be a completely general fact about quantum physics. That makes `h"/"2pi` a pretty important number, so we define the abbreviation . This symbol is read “h-bar.”
quantization of angular momentum

self-check:
What is the angular momentum of the wave function shown on page 985?
(answer in the back of the PDF version of the book)
36.1 Classifying states by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.