35.6 The Schrödinger equation by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
35.6 The Schrödinger equation (optional calculus-based section)
In section 35.5 we were able to apply conservation of energy to an electron's wavefunction, but only by using the clumsy graphical technique of osculating sine waves as a measure of the wave's curvature. You have learned a more convenient measure of curvature in calculus: the second derivative. To relate the two approaches, we take the second derivative of a sine wave:
`d^2/(dx^2)sin((2pix)/lambda)=d/(dx)((2pi)/lambdacos((2pix)/lambda)`
`=-((2pi)/lambda)^2sin((2pix)/lambda)`
Taking the second derivative gives us back the same function, but with a minus sign and a constant out in front that is related to the wavelength. We can thus relate the second derivative to the osculating wavelength:
[1] `(d^2Psi)/(dx^2) = -((2pi)/lambda )^2Psi `
This could be solved for `lambda` in terms of `Psi`, but it will turn out to be more convenient to leave it in this form.
Using conservation of energy, we have
` = p^2/(2m) + PE`
` = (h"/"lambda)^2/(2m) + PE`
Note that both equation [1] and equation [2] have `lambda^2` in the denominator. We can simplify our algebra by multiplying both sides of equation [2] by `Psi` to make it look more like equation [1]:
`E*Psi=(h"/"lambda)^2/(2m)Psi+PE*Psi`
`=1/(2m)(h/(2pi))^2((2pi)/lambda)^2Psi+PE*Psi`
`=-1/(2m)(h/(2pi))^2(d^2Psi)/(dx^2)+PE*Psi`
Further simplification is achieved by using the symbol `?` (`h` with a slash through it, read “h-bar”) as an abbreviation for `h"/"(2pi)`. We then have the important result known as the {Schrödinger equation}:
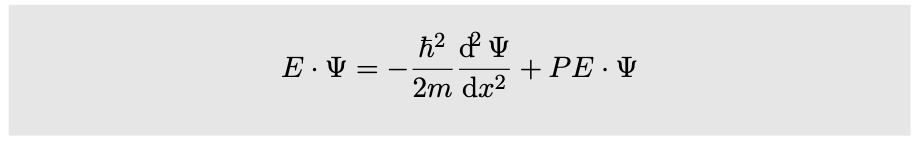
(Actually this is a simplified version of the Schrödinger equation, applying only to standing waves in one dimension.) Physically it is a statement of conservation of energy. The total energy `E` must be constant, so the equation tells us that a change in potential energy must be accompanied by a change in the curvature of the wave function. This change in curvature relates to a change in wavelength, which corresponds to a change in momentum and kinetic energy.
self-check:
Considering the assumptions that were made in deriving the Schrödinger equation, would it be correct to apply it to a photon? To an electron moving at relativistic speeds?
(answer in the back of the PDF version of the book)
Usually we know right off the bat how the potential energy depends on `x`, so the basic mathematical problem of quantum physics is to find a function `Psi(x)` that satisfies the Schrödinger equation for a given function `PE(x)`. An equation, such as the Schrödinger equation, that specifies a relationship between a function and its derivatives is known as a differential equation.
The study of differential equations in general is beyond the mathematical level of this book, but we can gain some important insights by considering the easiest version of the Schrödinger equation, in which the potential energy is constant. We can then rearrange the Schrödinger equation as follows:
`(d^2Psi)/(dx^2)=(2m(PE-E))/?^2Psi`,
which boils down to
`(d^2Psi)/(dx^2)=aPsi`
 where, according to our assumptions, `a` is independent of `x`. We need to find a function whose second derivative is the same as the original function except for a multiplicative constant. The only functions with this property are sine waves and exponentials:
where, according to our assumptions, `a` is independent of `x`. We need to find a function whose second derivative is the same as the original function except for a multiplicative constant. The only functions with this property are sine waves and exponentials:
`d^2/(dx^2)[qsin(rx+s)]=-qr^2sin(rx+s)`
`d^2/(dx^2)[qe^(rx+s)]=qr^2e^(rx+s)`
The sine wave gives negative values of `a`, ` a=-r^2`, and the exponential gives positive ones, `a=r^2`. The former applies to the classically allowed region with `PE<E`.
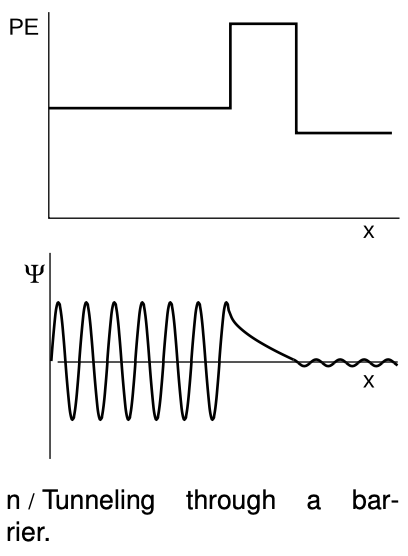
This leads us to a quantitative calculation of the tunneling effect discussed briefly in the preceding subsection.The wavefunction evidently tails off exponentially in the classically forbidden region. Suppose, as shown in figure n, a wave-particle traveling to the right encounters a barrier that it is classically forbidden to enter. Although the form of the Schrödinger equation we're using technically does not apply to traveling waves (because it makes no reference to time), it turns out that we can still use it to make a reasonable calculation of the probability that the particle will make it through the barrier. If we let the barrier's width be ww, then the ratio of the wave function on the left side of the barrier to the wave function on the right is
`(qe^(rx+s))/(qe^(r(x+w)+s))=e^(-rw).`
Probabilities are proportional to the squares of wave functions, so the probability of making it through the barrier is
`P=e^(-2rw)`
`=exp(-(2w)/? sqrt(2m(PE-E)) )`
self-check:
If we were to apply this equation to find the probability that a person can walk through a wall, what would the small value of Planck's constant imply?
(answer in the back of the PDF version of the book)
Use of complex numbers
In a classically forbidden region, a particle's total energy, `PE+KE`, is less than its `PE`, so its `KE` must be negative. If we want to keep believing in the equation `KE=p^2/(2m)`, then apparently the momentum of the particle is the square root of a negative number. This is a symptom of the fact that the Schrödinger equation fails to describe all of nature unless the wave function and various other quantities are allowed to be complex numbers. In particular it is not possible to describe traveling waves correctly without using complex wave functions.
This may seem like nonsense, since real numbers are the only ones that are, well, real! Quantum mechanics can always be related to the real world, however, because its structure is such that the results of measurements always come out to be real numbers. For example, we may describe an electron as having non-real momentum in classically forbidden regions, but its average momentum will always come out to be real (the imaginary parts average out to zero), and it can never transfer a non-real quantity of momentum to another particle.
A complete investigation of these issues is beyond the scope of this book, and this is why we have normally limited ourselves to standing waves, which can be described with real-valued wave functions.
35.6 The Schrödinger equation by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.