35.5 Electrons in electric fields by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
35.5 Electrons in electric fields
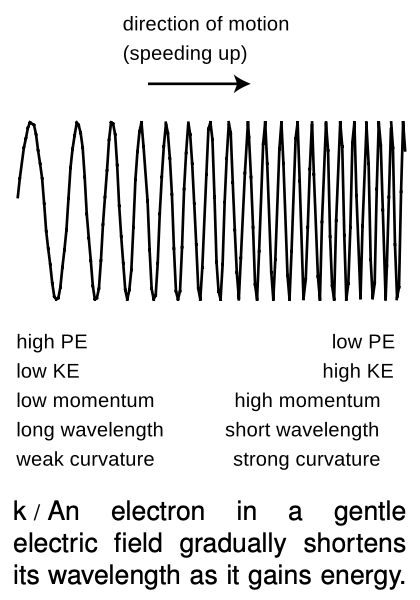 So far the only electron wave patterns we've considered have been simple sine waves, but whenever an electron finds itself in an electric field, it must have a more complicated wave pattern. Let's consider the example of an electron being accelerated by the electron gun at the back of a TV tube. The electron is moving from a region of low voltage into a region of higher voltage. Since its charge is negative, it loses `PE` by moving to a higher voltage, so its `KE` increases. As its potential energy goes down, its kinetic energy goes up by an equal amount, keeping the total energy constant. Increasing kinetic energy implies a growing momentum, and therefore a shortening wavelength, k.
So far the only electron wave patterns we've considered have been simple sine waves, but whenever an electron finds itself in an electric field, it must have a more complicated wave pattern. Let's consider the example of an electron being accelerated by the electron gun at the back of a TV tube. The electron is moving from a region of low voltage into a region of higher voltage. Since its charge is negative, it loses `PE` by moving to a higher voltage, so its `KE` increases. As its potential energy goes down, its kinetic energy goes up by an equal amount, keeping the total energy constant. Increasing kinetic energy implies a growing momentum, and therefore a shortening wavelength, k.
The wavefunction as a whole does not have a single well-defined wavelength, but the wave changes so gradually that if you only look at a small part of it you can still pick out a wavelength and relate it to the momentum and energy. (The picture actually exaggerates by many orders of magnitude the rate at which the wavelength changes.)
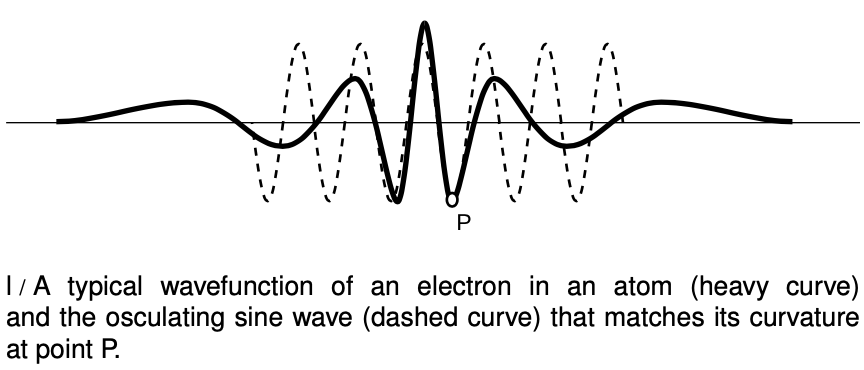
But what if the electric field was stronger? The electric field in a TV is only `~10^5 N"/"C`, but the electric field within an atom is more like `10^(12) N"/"C`. In figure l, the wavelength changes so rapidly that there is nothing that looks like a sine wave at all. We could get a general idea of the wavelength in a given region by measuring the distance between two peaks, but that would only be a rough approximation. Suppose we want to know the wavelength at point P. The trick is to construct a sine wave, like the one shown with the dashed line, which matches the curvature of the actual wave function as closely as possible near P. The sine wave that matches as well as possible is called the “osculating” curve, from a Latin word meaning “to kiss.” The wavelength of the osculating curve is the wavelength that will relate correctly to conservation of energy.
 Tunneling
Tunneling
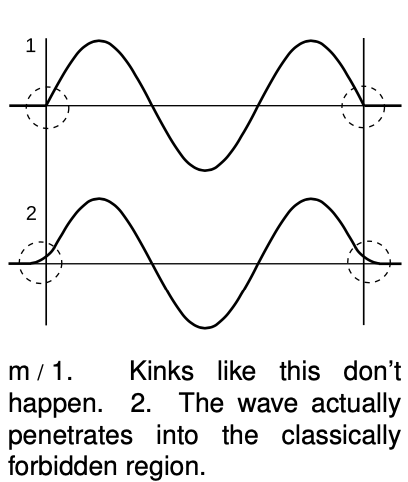
We implicitly assumed that the particle-in-a-box wave function would cut off abruptly at the sides of the box, m/1, but that would be unphysical. A kink has infinite curvature, and curvature is related to energy, so it can't be infinite. A physically realistic wave function must always “tail off” gradually, m/2. In classical physics, a particle can never enter a region in which its potential energy would be greater than the amount of energy it has available. But in quantum physics the wave function will always have a tail that reaches into the classically forbidden region. If it was not for this effect, called tunneling, the fusion reactions that power the sun would not occur due to the high potential energy that nuclei need in order to get close together! Tunneling is discussed in more detail in the next section.
35.5 Electrons in electric fields by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.