35.4 The uncertainty principle by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
35.4 The uncertainty principle
The uncertainty principle
 Eliminating randomness through measurement?
Eliminating randomness through measurement?
A common reaction to quantum physics, among both early-twentieth-century physicists and modern students, is that we should be able to get rid of randomness through accurate measurement. If I say, for example, that it is meaningless to discuss the path of a photon or an electron, you might suggest that we simply measure the particle's position and velocity many times in a row. This series of snapshots would amount to a description of its path.
A practical objection to this plan is that the process of measurement will have an effect on the thing we are trying to measure. This may not be of much concern, for example, when a traffic cop measures your car's motion with a radar gun, because the energy and momentum of the radar pulses aren't enough to change the car's motion significantly. But on the subatomic scale it is a very real problem. Making a videotape of an electron orbiting a nucleus is not just difficult, it is theoretically impossible, even with the video camera hooked up to the best imaginable microscope. The video camera makes pictures of things using light that has bounced off them and come into the camera. If even a single photon of the right wavelength was to bounce off of the electron we were trying to study, the electron's recoil would be enough to change its behavior significantly (see homework problem 4).
The Heisenberg uncertainty principle
This insight, that measurement changes the thing being measured, is the kind of idea that clove-cigarette-smoking intellectuals outside of the physical sciences like to claim they knew all along. If only, they say, the physicists had made more of a habit of reading literary journals, they could have saved a lot of work. The anthropologist Margaret Mead has recently been accused of inadvertently encouraging her teenaged Samoan informants to exaggerate the freedom of youthful sexual experimentation in their society. If this is considered a damning critique of her work, it is because she could have done better: other anthropologists claim to have been able to eliminate the observer-as-participant problem and collect untainted data.
The German physicist Werner Heisenberg, however, showed that in quantum physics, any measuring technique runs into a brick wall when we try to improve its accuracy beyond a certain point. Heisenberg showed that the limitation is a question of what there is to be known, even in principle, about the system itself, not of the inability of a particular measuring device to ferret out information that is knowable.
Suppose, for example, that we have constructed an electron in a box (quantum dot) setup in our laboratory, and we are able to adjust the length `L` of the box as desired. All the standing wave patterns pretty much fill the box, so our knowledge of the electron's position is of limited accuracy. If we write `Deltax` for the range of uncertainty in our knowledge of its position, then `Deltax` is roughly the same as the length of the box:
`DeltaxapproxL`
If we wish to know its position more accurately, we can certainly squeeze it into a smaller space by reducing `L`, but this has an unintended side-effect. A standing wave is really a superposition of two traveling waves going in opposite directions. The equation `p=h/lambda` only gives the magnitude of the momentum vector, not its direction, so we should really interpret the wave as a `50`/`50` mixture of a right-going wave with momentum `p=h/lambda` and a left-going one with momentum `p=-h/lambda`. The uncertainty in our knowledge of the electron's momentum is `p=(2h)/lambda`, covering the range between these two values. Even if we make sure the electron is in the ground state, whose wavelength `lambda=2L` is the longest possible, we have an uncertainty in momentum of `p=h/L`. In general, we find
`Deltap ≳ h"/"L`,
with equality for the ground state and inequality for the higher-energy states. Thus if we reduce `L` to improve our knowledge of the electron's position, we do so at the cost of knowing less about its momentum. This trade-off is neatly summarized by multiplying the two equations to give
`DeltapDeltax≳h.`
Although we have derived this in the special case of a particle in a box, it is an example of a principle of more general validity:
(This approximation can be made into a strict inequality, `DeltapDeltax>h"/"(4pi)`, but only with more careful definitions, which we will not bother with.1)
Note that although I encouraged you to think of this derivation in terms of a specific real-world system, the quantum dot, I never made any reference to specific measuring equipment. The argument is simply that we cannot know the particle's position very accurately unless it has a very well defined position, it cannot have a very well defined position unless its wave-pattern covers only a very small amount of space, and its wave-pattern cannot be thus compressed without giving it a short wavelength and a correspondingly uncertain momentum. The uncertainty principle is therefore a restriction on how much there is to know about a particle, not just on what we can know about it with a certain technique.
Example 6: An estimate for electrons in atoms
`=>` A typical energy for an electron in an atom is on the order of `(1 "volt")*e`, which corresponds to a speed of about `1%` of the speed of light. If a typical atom has a size on the order of `0.1` nm, how close are the electrons to the limit imposed by the uncertainty principle?
`=>` If we assume the electron moves in all directions with equal probability, the uncertainty in its momentum is roughly twice its typical momentum. This only an order-of-magnitude estimate, so we take `Deltap` to be the same as a typical momentum:
`DeltapDeltax=p_"typical"Deltax`
`=(m_"electron")(0.01c)(0.1×10^(-9) m)`
`=3×10^(-34) J*s`
This is on the same order of magnitude as Planck's constant, so evidently the electron is “right up against the wall.” (The fact that it is somewhat less than `h` is of no concern since this was only an estimate, and we have not stated the uncertainty principle in its most exact form.)
self-check:
If we were to apply the uncertainty principle to human-scale objects, what would be the significance of the small numerical value of Planck's constant?
(answer in the back of the PDF version of the book)self-check:
Suppose rain is falling on your roof, and there is a tiny hole that lets raindrops into your living room now and then. All these drops hit the same spot on the floor, so they have the same value of `x`. Not only that, but if the rain is falling straight down, they all have zero horizontal momentum. Thus it seems that the raindrops have `Deltap=0`, `Deltax=0`, and `DeltapDeltax=0`, violating the uncertainty principle. To look for the hole in this argument, consider how it would be acted out on the microscopic scale: an electron wave comes along and hits a narrow slit. What really happens?
(answer in the back of the PDF version of the book)
Measurement and Schrödinger's cat
In chapter 34 I briefly mentioned an issue concerning measurement that we are now ready to address carefully. If you hang around a laboratory where quantum-physics experiments are being done and secretly record the physicists' conversations, you'll hear them say many things that assume the probability interpretation of quantum mechanics. Usually they will speak as though the randomness of quantum mechanics enters the picture when something is measured. In the digital camera experiments of chapter 34, for example, they would casually describe the detection of a photon at one of the pixels as if the moment of detection was when the photon was forced to “make up its mind.” Although this mental cartoon usually works fairly well as a description of things one experiences in the lab, it cannot ultimately be correct, because it attributes a special role to measurement, which is really just a physical process like all other physical processes.2
If we are to find an interpretation that avoids giving any special role to measurement processes, then we must think of the entire laboratory, including the measuring devices and the physicists themselves, as one big quantum-mechanical system made out of protons, neutrons, electrons, and photons. In other words, we should take quantum physics seriously as a description not just of microscopic objects like atoms but of human-scale (“macroscopic”) things like the apparatus, the furniture, and the people.
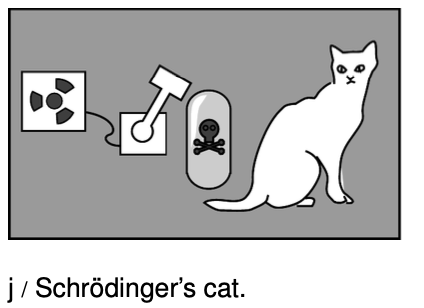 The most celebrated example is called the Schrödinger's cat experiment. Luckily for the cat, there probably was no actual experiment `-` it was simply a “thought experiment” that the German theorist Schrödinger discussed with his colleagues. Schrödinger wrote:
The most celebrated example is called the Schrödinger's cat experiment. Luckily for the cat, there probably was no actual experiment `-` it was simply a “thought experiment” that the German theorist Schrödinger discussed with his colleagues. Schrödinger wrote:
One can even construct quite burlesque cases. A cat is shut up in a steel container, together with the following diabolical apparatus (which one must keep out of the direct clutches of the cat): In a [radiation detector] there is a tiny mass of radioactive substance, so little that in the course of an hour perhaps one atom of it disintegrates, but also with equal probability not even one;if it does happen, the [detector] responds and ...activates a hammer that shatters a little flask of prussic acid [filling the chamber with poison gas]. If one has left this entire system to itself for an hour, then one will say to himself that the cat is still living, if in that time no atom has disintegrated. The first atomic disintegration would have poisoned it.
Now comes the strange part. Quantum mechanics says that the particles the cat is made of have wave properties, including the property of superposition. Schrödinger describes the wave function of the box's contents at the end of the hour:
The wave function of the entire system would express this situation by having the living and the dead cat mixed ... in equal parts [50/50 proportions]. The uncertainty originally restricted to the atomic domain has been transformed into a macroscopic uncertainty...
At first Schrödinger's description seems like nonsense. When you opened the box, would you see two ghost like cats, as in a doubly exposed photograph, one dead and one alive? Obviously not. You would have a single, fully material cat, which would either be dead or very, very upset. But Schrödinger has an equally strange and logical answer for that objection. In the same way that the quantum randomness of the radioactive atom spread to the cat and made its wave function a random mixture of life and death, the randomness spreads wider once you open the box, and your own wave function becomes a mixture of a person who has just killed a cat and a person who hasn't.3
Discussion Questions
A Compare `Deltap` and `Deltax` for the two lowest energy levels of the one-dimensional particle in a box, and discuss how this relates to the uncertainty principle.
B On a graph of`Deltap` versus `Deltax`, sketch the regions that are allowed and forbidden by the Heisenberg uncertainty principle. Interpret the graph: Where does an atom lie on it? An elephant? Can either `p` or `x` be measured with perfect accuracy if we don't care about the other?
35.4 The uncertainty principle by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
