34.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Selected vocabulary
photon — a particle of light
photoelectric effect — the ejection, by a photon, of an electron from the surface of an object
wave-particle duality — the idea that light is both a wave and a particle
Summary
Around the turn of the twentieth century, experiments began to show problems with the classical wave theory of light. In any experiment sensitive enough to detect very small amounts of light energy, it becomes clear that light energy cannot be divided into chunks smaller than a certain amount. Measurements involving the photoelectric effect demonstrate that this smallest unit of light energy equals `hf`, where `f` is the frequency of the light and `h` is a number known as Planck's constant. We say that light energy is quantized in units of `hf`, and we interpret this quantization as evidence that light has particle properties as well as wave properties. Particles of light are called photons.
The only method of reconciling the wave and particle natures of light that has stood the test of experiment is the probability interpretation: the probability that the particle is at a given location is proportional to the square of the amplitude of the wave at that location.
One important consequence of wave-particle duality is that we must abandon the concept of the path the particle takes through space. To hold on to this concept, we would have to contradict the well established wave nature of light, since a wave can spread out in every direction simultaneously.
Homework Problems
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
For some of these homework problems, you may find it convenient to refer to the diagram of the electromagnetic spectrum shown on p. 691.
1. Give a numerical comparison of the number of photons per second emitted by a hundred-watt FM radio transmitter and a hundred-watt lightbulb. `sqrt`
2. Two different flashes of light each have the same energy. One consists of photons with a wavelength of `600` nm, the other `400` nm. If the number of photons in the `600`-nm flash is `3.0×10^18`, how many photons are in the `400`-nm flash? `sqrt`
3. When light is reflected from a mirror, perhaps only `80%` of the energy comes back. The rest is converted to heat. One could try to explain this in two different ways: (1) `80%` of the photons are reflected, or (2) all the photons are reflected, but each loses `20%` of its energy. Based on your everyday knowledge about mirrors, how can you tell which interpretation is correct? [Based on a problem from PSSC Physics.]
4. Suppose we want to build an electronic light sensor using an apparatus like the one described in section 34.2 on p. 944. How would its ability to detect different parts of the spectrum depend on the type of metal used in the capacitor plates?
5. The photoelectric effect can occur not just for metal cathodes but for any substance, including living tissue. Ionization of DNA molecules can cause cancer or birth defects. If the energy required to ionize DNA is on the same order of magnitude as the energy required to produce the photoelectric effect in a metal, which of these types of electromagnetic waves might pose such a hazard? Explain.
- `60` Hz waves from power lines
- `100` MHz FM radio
- `1900` MHz radio waves from a cellular phone
- `2450` MHz microwaves from a microwave oven
- visible light
- ultraviolet light
- x-rays
6. The beam of a `100`-W overhead projector covers an area of `1 m×1 m` when it hits the screen 3 m away. Estimate the number of photons that are in flight at any given time. (Since this is only an estimate, we can ignore the fact that the beam is not parallel.)
 7. The two diffraction patterns were made by sending a flash of light through the same double slit. Give a numerical comparison of the amounts of energy in the two flashes. `sqrt`
7. The two diffraction patterns were made by sending a flash of light through the same double slit. Give a numerical comparison of the amounts of energy in the two flashes. `sqrt`
8. Three of the four graphs are properly normalized to represent single photons. Which one isn't? Explain.
9. Photon Fred has a greater energy than photon Ginger. For each of the following quantities, explain whether Fred's value of that quantity is greater than Ginger's, less than Ginger's, or equal to Ginger's. If there is no way to tell, explain why.
- frequency
- speed
- wavelength
- period
- electric field strength
- magnetic field strength
10. Give experimental evidence to disprove the following interpretation of wave-particle duality: A photon is really a particle, but it travels along a wavy path, like a zigzag with rounded corners. Cite a specific, real experiment.
11. In the photoelectric effect, electrons are observed with virtually no time delay`(-10 ns)`, even when the light source is very weak. (A weak light source does however only produce a small number of ejected electrons.) The purpose of this problem is to show that the lack of a significant time delay contradicted the classical wave theory of light, so throughout this problem you should put yourself in the shoes of a classical physicist and pretend you don't know about photons at all. At that time, it was thought that the electron might have a radius on the order of `10^(-15) m`. (Recent experiments have shown that if the electron has any finite size at all, it is far smaller.)
(a) Estimate the power that would be soaked up by a single electron in a beam of light with an intensity of `1 mW"/"m^2`. `sqrt`
(b) The energy, `E_s`, required for the electron to escape through the surface of the cathode is on the order of `10^(-19) J`. Find how long it would take the electron to absorb this amount of energy, and explain why your result constitutes strong evidence that there is something wrong with the classical theory. `sqrt`
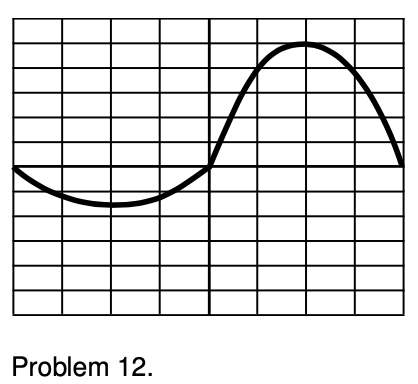 12. Many radio antennas are designed so that they preferentially emit or receive electromagnetic waves in a certain direction. However, no antenna is perfectly directional. The wave shown in the figure represents a single photon being emitted by an antenna at the center. The antenna is directional, so there is a stronger wave on the right than on the left. What is the probability that the photon will be observed on the right?
12. Many radio antennas are designed so that they preferentially emit or receive electromagnetic waves in a certain direction. However, no antenna is perfectly directional. The wave shown in the figure represents a single photon being emitted by an antenna at the center. The antenna is directional, so there is a stronger wave on the right than on the left. What is the probability that the photon will be observed on the right?
13. (a) A radio transmitter radiates power `P` in all directions, so that the energy spreads out spherically. Find the energy density at a distance `r`. `sqrt`
(b) Let the wavelength be `lambda`. As described in example 2 on p. 947, find the number of photons in a volume `lambda^3` at this distance `r`. `sqrt`
(c) For a `1000` kHz AM radio transmitting station, assuming reasonable values of `P` and `r`, verify, as claimed in the example, that the result from part b is very large.
34.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.