33.6 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
probability — the likelihood that something will happen, expressed as a number between zero and one
normalization — the property of probabilities that the sum of the probabilities of all possible outcomes must equal one
independence — the lack of any relationship between two random events
probability distribution — a curve that specifies the probabilities of various random values of a variable; areas under the curve correspond to probabilities
FWHM — the full width at half-maximum of a probability distribution; a measure of the width of the distribution
half-life — the amount of time that a radioactive atom will survive with probability 1/2 without decaying
Notation
`P` — probability
`t_(1"/"2)` — half-life
`D` — a probability distribution (used only in optional section 33.5; not a standardized notation)
Summary
Quantum physics differs from classical physics in many ways, the most dramatic of which is that certain processes at the atomic level, such as radioactive decay, are random rather than deterministic. There is a method to the madness, however: quantum physics still rules out any process that violates conservation laws, and it also offers methods for calculating probabilities numerically.
In this chapter we focused on certain generic methods of working with probabilities, without concerning ourselves with any physical details. Without knowing any of the details of radioactive decay, for example, we were still able to give a fairly complete treatment of the relevant probabilities. The most important of these generic methods is the law of independent probabilities, which states that if two random events are not related in any way, then the probability that they will both occur equals the product of the two probabilities,
probability of `A` and `B` = `P_AP_B` [if `A` and `B` are independent].
The most important application is to radioactive decay. The time that a radioactive atom has a `50%` chance of surviving is called the half-life, `t_(1"/"2)`. The probability of surviving for two half-lives is `(1"/"2)(1"/"2)=1"/"4`, and so on. In general, the probability of surviving a time `t` is given by
`P_(surv)(t)=0.5^(t"/"t_(1"/"2))`.
Related quantities such as the rate of decay and probability distribution for the time of decay are given by the same type of exponential function, but multiplied by certain constant factors.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. If a radioactive substance has a half-life of one year, does this mean that it will be completely decayed after two years? Explain.
2. Many individuals carry the recessive gene for albinism, but they are not albino unless they receive the gene from both their parents. In the U.S., an individual's probability of receiving the gene from a given parent is about 0.014. What is the probability that a given child will be born albino? `sqrt`
3. Problem 3 has been deleted.
4. Use a calculator to check the approximation that
`a^bapprox1+blna`,
if `b≪1`, using some arbitrary numbers. Then see how good the approximation is for values of `b` that are not quite as small compared to one.
5. Make up an example of a numerical problem involving a rate of decay where `Deltat≪t_(1"/"2)`, but the exact expression for the rate of decay on page 929 can still be evaluated on a calculator without getting something that rounds off to zero. Check that you get approximately the same result using both methods on pp. 929-930 to calculate the number of decays between `t` and `t+Deltat`. Keep plenty of significant figures in your results, in order to show the difference between them.
6. Devise a method for testing experimentally the hypothesis that a gambler's chance of winning at craps is independent of her previous record of wins and losses. If you don't invoke the mathematical definition of statistical independence, then you haven't proposed a test.
7. Refer to the probability distribution for people's heights in figure f on page 924.
(a) Show that the graph is properly normalized.
(b) Estimate the fraction of the population having heights between 140 and 150 cm. `sqrt`
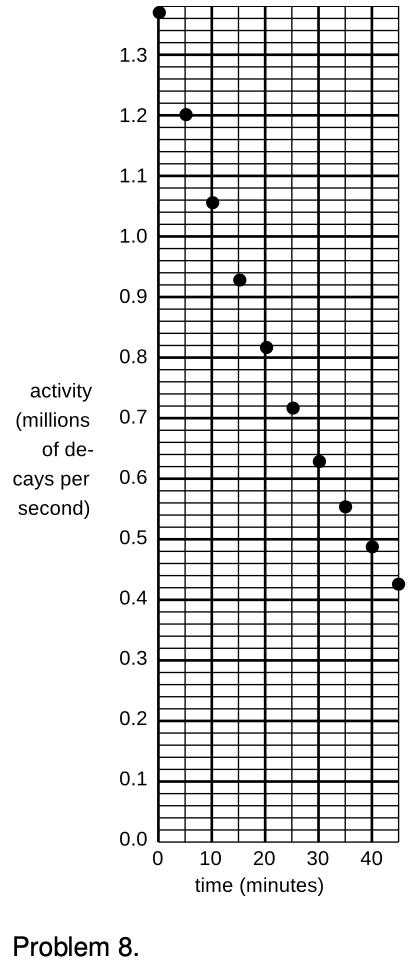 8. (a) A nuclear physicist is studying a nuclear reaction caused in an accelerator experiment, with a beam of ions from the accelerator striking a thin metal foil and causing nuclear reactions when a nucleus from one of the beam ions happens to hit one of the nuclei in the target. After the experiment has been running for a few hours, a few billion radioactive atoms have been produced, embedded in the target. She does not know what nuclei are being produced, but she suspects they are an isotope of some heavy element such as Pb, Bi, Fr or U. Following one such experiment, she takes the target foil out of the accelerator, sticks it in front of a detector, measures the activity every 5 min, and makes a graph (figure). The isotopes she thinks may have been produced are:
8. (a) A nuclear physicist is studying a nuclear reaction caused in an accelerator experiment, with a beam of ions from the accelerator striking a thin metal foil and causing nuclear reactions when a nucleus from one of the beam ions happens to hit one of the nuclei in the target. After the experiment has been running for a few hours, a few billion radioactive atoms have been produced, embedded in the target. She does not know what nuclei are being produced, but she suspects they are an isotope of some heavy element such as Pb, Bi, Fr or U. Following one such experiment, she takes the target foil out of the accelerator, sticks it in front of a detector, measures the activity every 5 min, and makes a graph (figure). The isotopes she thinks may have been produced are:
| isotope | half-life (minutes) |
| 211Pb | 36.1 |
| 214Pb | 26.8 |
| 214Bi | 19.7 |
| 223Fr | 21.8 |
| 239U | 23.5 |
Which one is it?
(b) Having decided that the original experimental conditions produced one specific isotope, she now tries using beams of ions traveling at several different speeds, which may cause different reactions. The following table gives the activity of the target 10, 20 and 30 minutes after the end of the experiment, for three different ion speeds.
| activity (millions of decays/s) after… | |||
| 10 min | 20 min | 30 min | |
| first ion speed | 1.933 | 0.832 | 0.382 |
| second ion speed | 1.200 | 0.545 | 0.248 |
| third ion speed | 7.211 | 1.296 | 0.248 |
Since such a large number of decays is being counted, assume that the data are only inaccurate due to rounding off when writing down the table. Which are consistent with the production of a single isotope, and which imply that more than one isotope was being created?
9. All helium on earth is from the decay of naturally occurring heavy radioactive elements such as uranium. Each alpha particle that is emitted ends up claiming two electrons, which makes it a helium atom. If the original 238U, atom is in solid rock (as opposed to the earth's molten regions), the He atoms are unable to diffuse out of the rock. This problem involves dating a rock using the known decay properties of uranium 238. Suppose a geologist finds a sample of hardened lava, melts it in a furnace, and finds that it contains 1230 mg of uranium and 2.3 mg of helium. 238U, decays by alpha emission, with a half-life of `4.5×10^9` years. The subsequent chain of alpha and electron (beta) decays involves much shorter half-lives, and terminates in the stable nucleus 206Pb. (You may want to review alpha and beta decay.) Almost all natural uranium is 238U, and the chemical composition of this rock indicates that there were no decay chains involved other than that of 238U.
(a) How many alphas are emitted in decay chain of a single 238U atom?
[Hint: Use conservation of mass.]
(b) How many electrons are emitted per decay chain?
[Hint: Use conservation of charge.
(c) How long has it been since the lava originally hardened? `sqrt`
10. Physicists thought for a long time that bismuth-209 was the heaviest stable isotope. (Very heavy elements decay by alpha emission because of the strong electrical repulsion of all their protons.) However, a 2003 paper by Marcillac et al. describes an experiment in which bismuth-209 lost its claim to fame --- it actually undergoes alpha decay with a half-life of `1.9×10^19` years.
(a) After the alpha particle is emitted, what is the isotope left over?
(b) Compare the half-life to the age of the universe, which is about 14 billion years.
(c) A tablespoon of Pepto-Bismol contains about `4×10^20` bismuth-209 atoms. Once you've swallowed it, how much time will it take, on the average, before the first atomic decay? `sqrt`
11. A blindfolded person fires a gun at a circular target of radius `b`, and is allowed to continue firing until a shot actually hits it. Any part of the target is equally likely to get hit. We measure the random distance `r` from the center of the circle to where the bullet went in.
(a) Show that the probability distribution of `r` must be of the form `D(r)=kr`, where `k` is some constant. (Of course we have `D(r)=0` for `r>b`.)
(b) Determine `k` by requiring `D` to be properly normalized. `sqrt`
(c) Find the average value of `r`. `sqrt`
(d) Interpreting your result from part c, how does it compare with `b"/"2`? Does this make sense? Explain. `int`
12. We are given some atoms of a certain radioactive isotope, with half-life `t_(1"/"2)`. We pick one atom at random, and observe it for one half-life, starting at time zero. If it decays during that one-half-life period, we record the time `t` at which the decay occurred. If it doesn't, we reset our clock to zero and keep trying until we get an atom that cooperates. The final result is a `0<=t<=t_(1"/"2)`, with a distribution that looks like the usual exponential decay curve, but with its tail chopped off.
(a) Find the distribution `D(t)`, with the proper normalization. `sqrt`
(b) Find the average value of `t`. `sqrt`
(c) Interpreting your result from part b, how does it compare with `t_(1"/"2)"/"2`? Does this make sense? Explain. `int`
13. The speed, `v`, of an atom in an ideal gas has a probability distribution of the form `D(v)=bve^(-cv^2)`, where `0<=v<infty`, `c` relates to the temperature, and `b` is determined by normalization.
(a) Sketch the distribution.
(b) Find `b` in terms of `c`. `sqrt`
(c) Find the average speed in terms of `c`, eliminating `b`. (Don't try to do the indefinite integral, because it can't be done in closed form. The relevant definite integral can be found in tables or done with computer software.)(answer check available at lightandmatter.com) `sqrt` `int`
14. Neutrinos interact so weakly with normal matter that, of the neutrinos from the sun that enter the earth from the day side, only about `10^(-10)` of them fail to reemerge on the night side. From this fact, estimate the thickness of matter, in units of light-years, that would be required in order to block half of them. This “half-distance” is analogous to a half-life for radioactive decay.
33.6 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.