29.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
real image — a place where an object appears to be, because the rays diffusely reflected from any given point on the object have been bent so that they come back together and then spread out again from the new point
virtual image — like a real image, but the rays don't actually cross again; they only appear to have come from the point on the image
converging — describes an optical device that brings light rays closer to the optical axis
diverging — bends light rays farther from the optical axis
magnification — the factor by which an image's linear size is increased (or decreased)
angular magnification — the factor by which an image's apparent angular size is increased (or decreased)
concave — describes a surface that is hollowed out like a cave
convex — describes a surface that bulges outward
Notation
`M` — the magnification of an image
`M_a` — the angular magnification of an image
Summary
A large class of optical devices, including lenses and flat and curved mirrors, operates by bending light rays to form an image. A real image is one for which the rays actually cross at each point of the image. A virtual image, such as the one formed behind a flat mirror, is one for which the rays only appear to have crossed at a point on the image. A real image can be projected onto a screen; a virtual one cannot.
Mirrors and lenses will generally make an image that is either smaller than or larger than the original object. The scaling factor is called the magnification. In many situations, the angular magnification is more important than the actual magnification.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. A man is walking at 1.0 m/s directly towards a flat mirror. At what speed is his separation from his image decreasing?
2. If a mirror on a wall is only big enough for you to see yourself from your head down to your waist, can you see your entire body by backing up? Test this experimentally and come up with an explanation for your observations, including a ray diagram.
Note that when you do the experiment, it's easy to confuse yourself if the mirror is even a tiny bit off of vertical. One way to check yourself is to artificially lower the top of the mirror by putting a piece of tape or a post-it note where it blocks your view of the top of your head. You can then check whether you are able to see more of yourself both above and below by backing up.
3. In this chapter we've only done examples of mirrors with hollowed-out shapes (called concave mirrors). Now draw a ray diagram for a curved mirror that has a bulging outward shape (called a convex mirror). (a) How does the image's distance from the mirror compare with the actual object's distance from the mirror? From this comparison, determine whether the magnification is greater than or less than one. (b) Is the image real, or virtual? Could this mirror ever make the other type of image?
4. As discussed in question 3, there are two types of curved mirrors, concave and convex. Make a list of all the possible combinations of types of images (virtual or real) with types of mirrors (concave and convex). (Not all of the four combinations are physically possible.) Now for each one, use ray diagrams to determine whether increasing the distance of the object from the mirror leads to an increase or a decrease in the distance of the image from the mirror.
Draw BIG ray diagrams! Each diagram should use up about half a page of paper.
Some tips: To draw a ray diagram, you need two rays. For one of these, pick the ray that comes straight along the mirror's axis, since its reflection is easy to draw. After you draw the two rays and locate the image for the original object position, pick a new object position that results in the same type of image, and start a new ray diagram, in a different color of pen, right on top of the first one. For the two new rays, pick the ones that just happen to hit the mirror at the same two places; this makes it much easier to get the result right without depending on extreme accuracy in your ability to draw the reflected rays.
5. If the user of an astronomical telescope moves her head closer to or farther away from the image she is looking at, does the magnification change? Does the angular magnification change? Explain. (For simplicity, assume that no eyepiece is being used.)
6. In figure g/2 in on page 836, only the image of my forehead was located by drawing rays. Either photocopy the figure or download the book and print out the relevant page. On this copy of the figure, make a new set of rays coming from my chin, and locate its image. To make it easier to judge the angles accurately, draw rays from the chin that happen to hit the mirror at the same points where the two rays from the forehead were shown hitting it. By comparing the locations of the chin's image and the forehead's image, verify that the image is actually upside-down, as shown in the original figure.
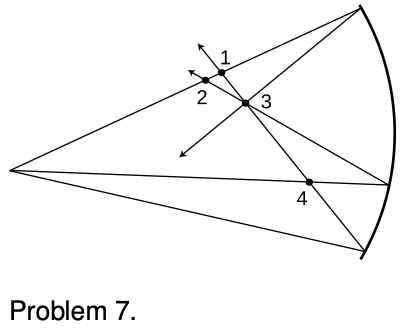 7. The figure shows four points where rays cross. Of these, which are image points? Explain.
7. The figure shows four points where rays cross. Of these, which are image points? Explain.
8. Here's a game my kids like to play. I sit next to a sunny window, and the sun reflects from the glass on my watch, making a disk of light on the wall or floor, which they pretend to chase as I move it around. Is the spot a disk because that's the shape of the sun, or because it's the shape of my watch? In other words, would a square watch make a square spot, or do we just have a circular image of the circular sun, which will be circular no matter what?
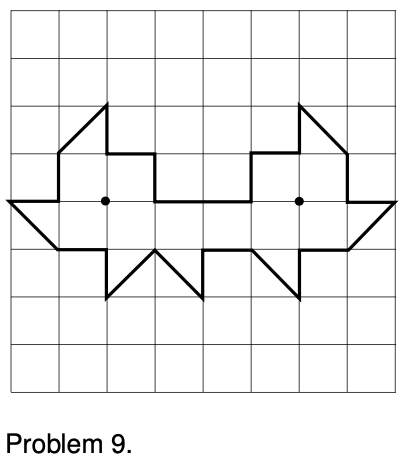 9. Suppose we have a polygonal room whose walls are mirrors, and there a point like light source in the room. In most such examples, every point in the room ends up being illuminated by the light source after some finite number of reflections. A difficult mathematical question, first posed in the middle of the last century, is whether it is ever possible to have an example in which the whole room is not illuminated. (Rays are assumed to be absorbed if they strike exactly at a vertex of the polygon, or if they pass exactly through the plane of a mirror.)
9. Suppose we have a polygonal room whose walls are mirrors, and there a point like light source in the room. In most such examples, every point in the room ends up being illuminated by the light source after some finite number of reflections. A difficult mathematical question, first posed in the middle of the last century, is whether it is ever possible to have an example in which the whole room is not illuminated. (Rays are assumed to be absorbed if they strike exactly at a vertex of the polygon, or if they pass exactly through the plane of a mirror.)
The problem was finally solved in 1995 by G.W. Tokarsky, who found an example of a room that was not illuminable from a certain point. Figure 9 shows a slightly simpler example found two years later by D. Castro. If a light source is placed at either of the locations shown with dots, the other dot remains unilluminated, although every other point is lit up. It is not straightforward to prove rigorously that Castro's solution has this property. However, the plausibility of the solution can be demonstrated as follows.
Suppose the light source is placed at the right-hand dot. Locate all the images formed by single reflections. Note that they form a regular pattern. Convince yourself that none of these images illuminates the left-hand dot. Because of the regular pattern, it becomes plausible that even if we form images of images, images of images of images, etc., none of them will ever illuminate the other dot.
There are various other versions of the problem, some of which remain unsolved. The book by Klee and Wagon gives a good introduction to the topic, although it predates Tokarsky and Castro's work. `***`
References:
G.W. Tokarsky, “Polygonal Rooms Not Illuminable from Every Point.” Amer. Math. Monthly 102, 867-879, 1995.
D. Castro, “Corrections.” Quantum 7, 42, Jan. 1997.
V. Klee and S. Wagon, Old and New Unsolved Problems in Plane Geometry and Number Theory. Mathematical Association of America, 1991.
Exercise 29: Exploring images with a curved mirror
Equipment:
- concave mirrors with deep curvature
- concave mirrors with gentle curvature
- convex mirrors
1. Obtain a curved mirror from your instructor. If it is silvered on both sides, make sure you're working with the concave side, which bends light rays inward. Look at your own face in the mirror. Now change the distance between your face and the mirror, and see what happens. Explore the full range of possible distances between your face and the mirror.
In these observations you've been changing two variables at once: the distance between the object (your face) and the mirror, and the distance from the mirror to your eye. In general, scientific experiments become easier to interpret if we practice isolation of variables, i.e., only change one variable while keeping all the others constant. In parts 2 and 3 you'll form an image of an object that's not your face, so that you can have independent control of the object distance and the point of view.
2. With the mirror held far away from you, observe the image of something behind you, over your shoulder. Now bring your eye closer and closer to the mirror. Can you see the image with your eye very close to the mirror? See if you can explain your observation by drawing a ray diagram.
3. Now imagine the following new situation, but don't actually do it yet. Suppose you lay the mirror face-up on a piece of tissue paper, put your finger a few cm above the mirror, and look at the image of your finger. As in part 2, you can bring your eye closer and closer to the mirror.
Will you be able to see the image with your eye very close to the mirror? Draw a ray diagram to help you predict what you will observe.
Prediction:__________________________________________
Now test your prediction. If your prediction was incorrect, see if you can figure out what went wrong, or ask your instructor for help.
4. For parts 4 and 5, it's more convenient to use concave mirrors that are more gently curved; obtain one from your instructor. Lay the mirror on the tissue paper, and use it to create an image of the overhead lights on a piece of paper above it and a little off to the side. What do you have to do in order to make the image clear? Can you explain this observation using a ray diagram?
5. Now imagine the following experiment, but don't do it yet. What will happen to the image on the paper if you cover half of the mirror with your hand?
Prediction:__________________________________________
Test your prediction. If your prediction was incorrect, can you explain what happened?
6. Now imagine forming an image with a convex mirror (one that bulges outward), and that therefore bends light rays away from the central axis (i.e., is diverging). Draw a typical ray diagram.
Is the image real, or virtual? Will there be more than one type of image?
Prediction:__________________________________________
Test your prediction.
29.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.