29.2 Curved mirrors by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

29.2 Curved mirrors

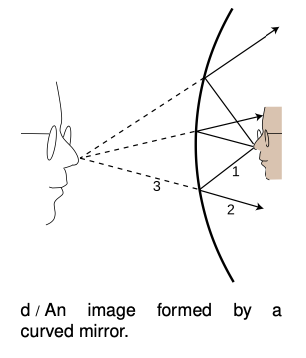An image in a flat mirror is a pretechnological example: even animals can look at their reflections in a calm pond. We now pass to our first nontrivial example of the manipulation of an image by technology: an image in a curved mirror. Before we dive in, let's consider why this is an important example. If it was just a question of memorizing a bunch of facts about curved mirrors, then you would rightly rebel against an effort to spoil the beauty of your liberally educated brain by force-feeding you technological trivia. The reason this is an important example is not that curved mirrors are so important in and of themselves, but that the results we derive for curved bowl-shaped mirrors turn out to be true for a large class of other optical devices, including mirrors that bulge outward rather than inward, and lenses as well. A microscope or a telescope is simply a combination of lenses or mirrors or both. What you're really learning about here is the basic building block of all optical devices from movie projectors to octopus eyes.

Because the mirror in figure d is curved, it bends the rays back closer together than a flat mirror would: we describe it as converging. Note that the term refers to what it does to the light rays, not to the physical shape of the mirror's surface . (The surface itself would be described as concave. The term is not all that hard to remember, because the hollowed-out interior of the mirror is like a cave.) It is surprising but true that all the rays like 3 really do converge on a point, forming a good image. We will not prove this fact, but it is true for any mirror whose curvature is gentle enough and that is symmetric with respect to rotation about the perpendicular line passing through its center (not asymmetric like a potato chip). The old-fashioned method of making mirrors and lenses is by grinding them in grit by hand, and this automatically tends to produce an almost perfect spherical surface.

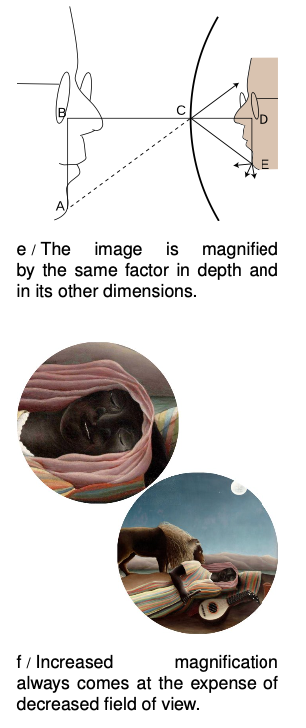
Bending a ray like 2 inward implies bending its imaginary continuation 3 outward, in the same way that raising one end of a seesaw causes the other end to go down. The image therefore forms deeper behind the mirror. This doesn't just show that there is extra distance between the image-nose and the mirror; it also implies that the image itself is bigger from front to back. It has been magnified in the front-to-back direction.

It is easy to prove that the same magnification also applies to the image's other dimensions. Consider a point like E in figure e. The trick is that out of all the rays diffusely reflected by `E`, we pick the one that happens to head for the mirror's center, `C`. The equal-angle property of specular reflection plus a little straightforward geometry easily leads us to the conclusion that triangles `ABC` and `CDE` are the same shape, with `ABC` being simply a scaled-up version of `CDE`. The magnification of depth equals the ratio `BC"/"CD`, and the up-down magnification is `AB"/"DE`. A repetition of the same proof shows that the magnification in the third dimension (out of the page) is also the same. This means that the image-head is simply a larger version of the real one, without any distortion. The scaling factor is called the magnification, `M`. The image in the figure is magnified by a factor `M=1.9`.

Note that we did not explicitly specify whether the mirror was a sphere, a paraboloid, or some other shape. However, we assumed that a focused image would be formed, which would not necessarily be true, for instance, for a mirror that was asymmetric or very deeply curved.

29.2 Curved mirrors by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.