28.4 Geometry of specular reflection by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
28.4 Geometry of specular reflection
To change the motion of a material object, we use a force. Is there any way to exert a force on a beam of light? Experiments show that electric and magnetic fields do not deflect light beams, so apparently light has no electric charge. Light also has no mass, so until the twentieth century it was believed to be immune to gravity as well. Einstein predicted that light beams would be very slightly deflected by strong gravitational fields, and he was proved correct by observations of rays of starlight that came close to the sun, but obviously that's not what makes mirrors and lenses work!
If we investigate how light is reflected by a mirror, we will find that the process is horrifically complex, but the final result is surprisingly simple. What actually happens is that the light is made of electric and magnetic fields, and these fields accelerate the electrons in the mirror. Energy from the light beam is momentarily transformed into extra kinetic energy of the electrons, but because the electrons are accelerating they re-radiate more light, converting their kinetic energy back into light energy. We might expect this to result in a very chaotic situation, but amazingly enough, the electrons move together to produce a new, reflected beam of light, which obeys two simple rules:
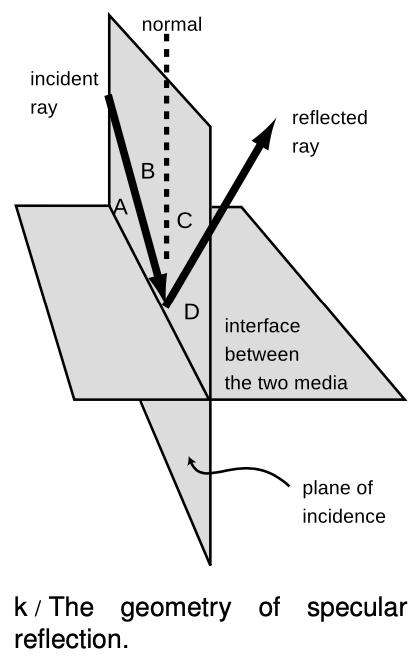 The angle of the reflected ray is the same as that of the incident ray.
The angle of the reflected ray is the same as that of the incident ray.- The reflected ray lies in the plane containing the incident ray and the normal (perpendicular) line. This plane is known as the plane of incidence.
The two angles can be defined either with respect to the normal, like angles `B` and `C` in the figure, or with respect to the reflecting surface, like angles `A` and `D`. There is a convention of several hundred years' standing that one measures the angles with respect to the normal, but the rule about equal angles can logically be stated either as `B=C` or as `A=D`.
The phenomenon of reflection occurs only at the boundary between two media, just like the change in the speed of light that passes from one medium to another. As we have seen in chapter 20, this is the way all waves behave.
Most people are surprised by the fact that light can be reflected back from a less dense medium. For instance, if you are diving and you look up at the surface of the water, you will see a reflection of yourself.
self-check:
Each of these diagrams is supposed to show two different rays being reflected from the same point on the same mirror. Which are correct, and which are incorrect?

Reversibility of light rays
The fact that specular reflection displays equal angles of incidence and reflection means that there is a symmetry: if the ray had come in from the right instead of the left in the figure above, the angles would have looked exactly the same. This is not just a pointless detail about specular reflection. It's a manifestation of a very deep and important fact about nature, which is that the laws of physics do not distinguish between past and future. Cannonballs and planets have trajectories that are equally natural in reverse, and so do light rays. This type of symmetry is called time-reversal symmetry.
Typically, time-reversal symmetry is a characteristic of any process that does not involve heat. For instance, the planets do not experience any friction as they travel through empty space, so there is no frictional heating. We should thus expect the time-reversed versions of their orbits to obey the laws of physics, which they do. In contrast, a book sliding across a table does generate heat from friction as it slows down, and it is therefore not surprising that this type of motion does not appear to obey time-reversal symmetry. A book lying still on a flat table is never observed to spontaneously start sliding, sucking up heat energy and transforming it into kinetic energy.
Similarly, the only situation we've observed so far where light does not obey time-reversal symmetry is absorption, which involves heat. Your skin absorbs visible light from the sun and heats up, but we never observe people's skin to glow, converting heat energy into visible light. People's skin does glow in infrared light, but that doesn't mean the situation is symmetric. Even if you absorb infrared, you don't emit visible light, because your skin isn't hot enough to glow in the visible spectrum.
These apparent heat-related asymmetries are not actual asymmetries in the laws of physics. The interested reader may wish to learn more about this from optional chapter 16 on thermodynamics.
Example 1: Ray tracing on a computer
A number of techniques can be used for creating artificial visual scenes in computer graphics. Figure l shows such a scene, which was created by the brute-force technique of simply constructing a very detailed ray diagram on a computer. This technique requires a great deal of computation, and is therefore too slow to be used for video games and computer-animated movies. One trick for speeding up the computation is to exploit the reversibility of light rays. If one was to trace every ray emitted by every illuminated surface, only a tiny fraction of those would actually end up passing into the virtual “camera,” and therefore almost all of the computational effort would be wasted. One can instead start a ray at the camera, trace it backward in time, and see where it would have come from. With this technique, there is no wasted effort.

 Discussion Questions
Discussion Questions
A If a light ray has a velocity vector with components `c_x` and `c_y`, what will happen when it is reflected from a surface that lies along the `y` axis? Make sure your answer does not imply a change in the ray's speed.
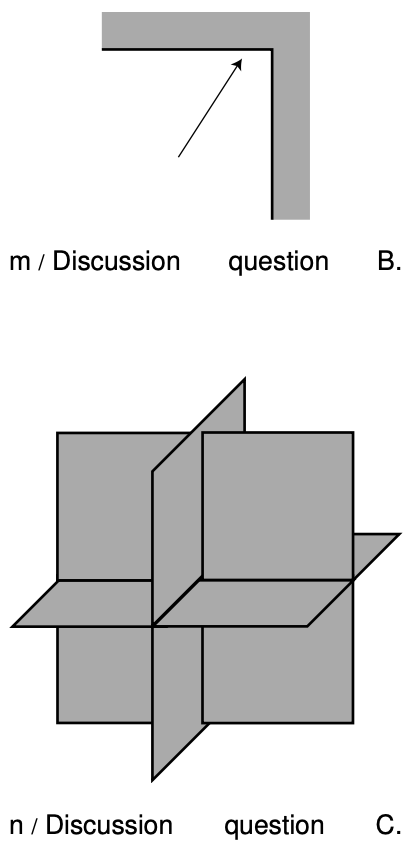
B Generalizing your reasoning from discussion question A, what will happen to the velocity components of a light ray that hits a corner, as shown in the figure, and undergoes two reflections?
C Three pieces of sheet metal arranged perpendicularly as shown in the figure form what is known as a radar corner. Let's assume that the radar corner is large compared to the wavelength of the radar waves, so that the ray model makes sense. If the radar corner is bathed in radar rays, at least some of them will undergo three reflections. Making a further generalization of your reasoning from the two preceding discussion questions, what will happen to the three velocity components of such a ray? What would the radar corner be useful for?
28.4 Geometry of specular reflection by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.