27.4 Cosmology by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
27.4 Cosmology
The Big Bang
Section 19.5 presented the evidence, discovered by Hubble, that the universe is expanding in the aftermath of the Big Bang: when we observe the light from distant galaxies, it is always Doppler-shifted toward the red end of the spectrum, indicating that no matter what direction we look in the sky, everything is rushing away from us. This seems to go against the modern attitude, originated by Copernicus, that we and our planet do not occupy a special place in the universe. Why is everything rushing away from our planet in particular? But general relativity shows that this anti-Copernican conclusion is wrong. General relativity describes space not as a rigidly defined background but as something that can curve and stretch, like a sheet of rubber. We imagine all the galaxies as existing on the surface of such a sheet, which then expands uniformly. The space between the galaxies (but not the galaxies themselves) grows at a steady rate, so that any observer, inhabiting any galaxy, will see every other galaxy as receding. There is therefore no privileged or special location in the universe.
We might think that there would be another kind of special place, which would be the one at which the Big Bang happened. Maybe someone has put a brass plaque there? But general relativity doesn't describe the Big Bang as an explosion that suddenly occurred in a preexisting background of time and space. According to general relativity, space itself came into existence at the Big Bang, and the hot, dense matter of the early universe was uniformly distributed everywhere. The Big Bang happened everywhere at once.
Observations show that the universe is very uniform on large scales, and for ease of calculation, the first physical models of the expanding universe were constructed with perfect uniformity. In these models, the Big Bang was a singularity. This singularity can't even be included as an event in spacetime, so that time itself only exists after the Big Bang. A Big Bang singularity also creates an even more acute version of the black hole information paradox. Whereas matter and information disappear into a black hole singularity, stuff pops out of a Big Bang singularity, and there is no physical principle that could predict what it would be.
As with black holes, there was considerable skepticism about whether the existence of an initial singularity in these models was an arifact of the unrealistically perfect uniformity assumed in the models. Perhaps in the real universe, extrapolation of all the paths of the galaxies backward in time would show them missing each other by millions of light-years. But in 1972 Stephen Hawking proved a variant on the Penrose singularity theorem that applied to Big Bang singularities. By the Hawking singularity theorem, the level of uniformity we see in the present-day universe is more than sufficient to prove that a Big Bang singularity must have existed.
The cosmic censorship hypothesis
It might not be too much of a philosophical jolt to imagine that information was spontaneously created in the Big Bang. Setting up the initial conditions of the entire universe is traditionally the prerogative of God, not the laws of physics. But there is nothing fundamental in general relativity that forbids the existence of other singularities that act like the Big Bang, being information producers rather than information consumers. As John Earman of the University of Pittsburgh puts it, anything could pop out of such a singularity, including green slime or your lost socks. This would eliminate any hope of finding a universal set of laws of physics that would be able to make a prediction given any initial situation.
That would be such a devastating defeat for the enterprise of physics that in 1969 Penrose proposed an alternative, humorously named the “cosmic censorship hypothesis,” which states that every singularity in our universe, other than the Big Bang, is hidden behind an event horizon. Therefore if green slime spontaneously pops out of one, there is limited impact on the predictive ability of physics, since the slime can never have any causal effect on the outside world. A singularity that is not modestly cloaked behind an event horizon is referred to as a naked singularity. Nobody has yet been able to prove the cosmic censorship hypothesis.
The advent of high-precision cosmology
We expect that if there is matter in the universe, it should have gravitational fields, and in the rubber-sheet analogy this should be represented as a curvature of the sheet. Instead of a flat sheet, we can have a spherical balloon, so that cosmological expansion is like inflating it with more and more air. It is also possible to have negative curvature, as in figure e on p. 797. All three of these are valid, possible cosmologies according to relativity. The positive-curvature type happens if the average density of matter in the universe is above a certain critical level, the negative-curvature one if the density is below that value.
 To find out which type of universe we inhabit, we could try to take a survey of the matter in the universe and determine its average density. Historically, it has been very difficult to do this, even to within an order of magnitude. Most of the matter in the universe probably doesn't emit light, making it difficult to detect. Astronomical distance scales are also very poorly calibrated against absolute units such as the SI.
To find out which type of universe we inhabit, we could try to take a survey of the matter in the universe and determine its average density. Historically, it has been very difficult to do this, even to within an order of magnitude. Most of the matter in the universe probably doesn't emit light, making it difficult to detect. Astronomical distance scales are also very poorly calibrated against absolute units such as the SI.
Instead, we measure the universe's curvature, and infer the density of matter from that. It turns out that we can do this by observing the cosmic microwave background (CMB) radiation, which is the light left over from the brightly glowing early universe, which was dense and hot. As the universe has expanded, light waves that were in flight have expanded their wavelengths along with it. This afterglow of the big bang was originally visible light, but after billions of years of expansion it has shifted into the microwave radio part of the electromagnetic spectrum. The CMB is not perfectly uniform, and this turns out to give us a way to measure the universe's curvature. Since the CMB was emitted when the universe was only about 400,000 years old, any vibrations or disturbances in the hot hydrogen and helium gas that filled space in that era would only have had time to travel a certain distance, limited by the speed of sound. We therefore expect that no feature in the CMB should be bigger than a certain known size. In a universe with negative spatial curvature, the sum of the interior angles of a triangle is less than the Euclidean value of 180 degrees. Therefore if we observe a variation in the CMB over some angle, the distance between two points on the sky is actually greater than would have been inferred from Euclidean geometry. The opposite happens if the curvature is positive.
This observation was done by the 1989-1993 COBE probe, and its 2001-2009 successor, the Wilkinson Microwave Anisotropy Probe. The result is that the angular sizes are almost exactly equal to what they should be according to Euclidean geometry. We therefore infer that the universe is very close to having zero average spatial curvature on the cosmological scale, and this tells us that its average density must be within about 0.5% of the critical value. The years since COBE and WMAP mark the advent of an era in which cosmology has gone from being a field of estimates and rough guesses to a high-precision science.
If one is inclined to be skeptical about the seemingly precise answers to the mysteries of the cosmos, there are consistency checks that can be carried out. In the bad old days of low-precision cosmology, estimates of the age of the universe ranged from 10 billion to 20 billion years, and the low end was inconsistent with the age of the oldest star clusters. This was believed to be a problem either for observational cosmology or for the astrophysical models used to estimate the ages of the clusters: “You can't be older than your ma.” Current data have shown that the low estimates of the age were incorrect, so consistency is restored. (The best figure for the age of the universe is currently `13.8+-0.1` billion years.)
Dark energy and dark matter
Not everything works out so smoothly, however. One surprise, discussed in section 10.6, is that the universe's expansion is not currently slowing down, as had been expected due to the gravitational attraction of all the matter in it. Instead, it is currently speeding up. This is attributed to a variable in Einstein's equations, long assumed to be zero, which represents a universal gravitational repulsion of space itself, occurring even when there is no matter present. The current name for this is “dark energy,” although the fancy name is just a label for our ignorance about what causes it.
Another surprise comes from attempts to model the formation of the elements during the era shortly after the Big Bang, before the formation of the first stars (section 26.4.10). The observed relative abundances of hydrogen, helium, and deuterium (2H) cannot be reconciled with the density of low-velocity matter inferred from the observational data. If the inferred mass density were entirely due to normal matter (i.e., matter whose mass consisted mostly of protons and neutrons), then nuclear reactions in the dense early universe should have proceeded relatively efficiently, leading to a much higher ratio of helium to hydrogen, and a much lower abundance of deuterium. The conclusion is that most of the matter in the universe must be made of an unknown type of exotic matter, known as “dark matter.” We are in the ironic position of knowing that precisely 96% of the universe is something other than atoms, but knowing nothing about what that something is. As of 2013, there have been several experiments that have been carried out to attempt the direct detection of dark matter particles. These are carried out at the bottom of mineshafts to eliminate background radiation. Early claims of success appear to have been statistical flukes, and the most sensitive experiments have not detected anything.2
Homework Problems
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. Prove, as claimed in the caption of figure a on p. 795, that `S-180°=4(s-180°)`, where `S` is the sum of the angles of the large equilateral triangle and `s` is the corresponding sum for one of the four small ones.
2. If a two-dimensional being lived on the surface of a cone, would it say that its space was curved, or not?
3. (a) Verify that the equation `1-gh"/"c^2` for the gravitational Doppler shift and gravitational time dilation has units that make sense. (b) Does this equation satisfy the correspondence principle?
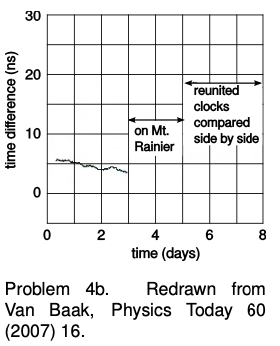 4. (a) Calculate the Doppler shift to be expected in the Pound-Rebka experiment described on p. 800. (b) In the 1978 Iijima mountain-valley experiment (p. 652), analysis was complicated by the clock's sensitivity to pressure, humidity, and temperature. A cleaner version of the experiment was done in 2005 by hobbyist Tom Van Baak. He put his kids and three of his atomic clocks in a minivan and drove from Bellevue, Washington to a lodge on Mount Rainier, 1340 meters higher in elevation. At home, he compared the clocks to others that had stayed at his house. Verify that the effect shown in the graph is as predicted by general relativity.
4. (a) Calculate the Doppler shift to be expected in the Pound-Rebka experiment described on p. 800. (b) In the 1978 Iijima mountain-valley experiment (p. 652), analysis was complicated by the clock's sensitivity to pressure, humidity, and temperature. A cleaner version of the experiment was done in 2005 by hobbyist Tom Van Baak. He put his kids and three of his atomic clocks in a minivan and drove from Bellevue, Washington to a lodge on Mount Rainier, 1340 meters higher in elevation. At home, he compared the clocks to others that had stayed at his house. Verify that the effect shown in the graph is as predicted by general relativity.
5. The International Space Station orbits at an altitude of about 350 km and a speed of about 8000 m/s relative to the ground. Compare the gravitational and kinematic time dilations. Over all, does time run faster on the ISS than on the ground, or more slowly?
6. Section 27.3 presented a Newtonian estimate of how compact an object would have to be in order to be a black hole. Although this estimate is not really right, it turns out to give the right answer to within about a factor of 2. To roughly what size would the earth have to be compressed in order to become a black hole?
7. Clock A sits on a desk. Clock B is tossed up in the air from the same height as the desk and then comes back down. Compare the elapsed times. (hint:tossed-clock)
8. The angular defect `d` of a triangle (measured in radians) is defined as `s-pi`, where `s` is the sum of the interior angles. The angular defect is proportional to the area `A` of the triangle. Consider the geometry measured by a two-dimensional being who lives on the surface of a sphere of radius `R`. First find some triangle on the sphere whose area and angular defect are easy to calculate. Then determine the general equation for `d` in terms of `A` and `R`. `sqrt`
Exercise 27: Misconceptions about relativity
The following is a list of common misconceptions about relativity. The class will be split up into random groups, and each group will cooperate on developing an explanation of the misconception, and then the groups will present their explanations to the class. There may be multiple rounds, with students assigned to different randomly chosen groups in successive rounds.
1. How can light have momentum if it has zero mass?
2. What does the world look like in a frame of reference moving at `c`?
3. Alice observes Betty coming toward her from the left at `c"/"2`, and Carol from the right at `c"/"2`. Therefore Betty is moving at the speed of light relative to Carol.
4. Are relativistic effects such as length contraction and time dilation real, or do they just seem to be that way?
5. Special relativity only matters if you've moving close to the speed of light.
6. Special relativity says that everything is relative.
7. There is a common misconception that relativistic length contraction is what we would actually see. Refute this by drawing a spacetime diagram for an object approaching an observer, and tracing rays of light emitted from the object's front and back that both reach the observer's eye at the same time.
8. When you travel close to the speed of light, your time slows down.
9. Is a light wave's wavelength relativistically length contracted by a factor of gamma?
10. Accelerate a baseball to ultrarelativistic speeds. Does it become a black hole?
11. Where did the Big Bang happen?
12. The universe can't be infinite in size, because it's only had a finite amount of time to expand from the point where the Big Bang happened.
27.4 Cosmology by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.