27.3 Black holes by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

27.3 Black holes

The observations described so far showed only small effects from curvature. To get a big effect, we should look at regions of space in which there are strong gravitational fields. The prime example is a black hole. The best studied examples are two objects in our own galaxy: Cygnus X-1, which is believed to be a black hole with about ten times the mass of our sun, and Sagittarius A*, an object near the center of our galaxy with about four million solar masses. (See problem 14, p. 277 for how we know Sagittarius A*'s mass.)

Although a black hole is a relativistic object, we can gain some insight into how it works by applying Newtonian physics. As shown in problem 21 on p. 349, a spherical body of mass `M` has an escape velocity `v=sqrt((2GM)/r)`, which is the minimum velocity that we would need to give to a projectile shot from a distance `r` so that it would never fall back down. If `r` is small enough, the escape velocity will be greater than `c`, so that even a ray of light can never escape.

We can now make an educated guess as to what this means without having to study all the mathematics of general 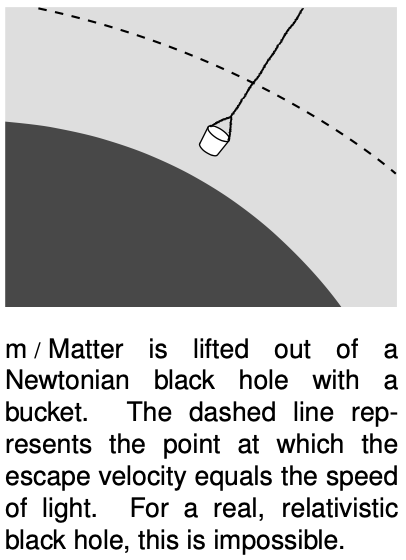relativity. In relativity, `c` isn't really the speed of light, it's really to be thought of as a restriction on how fast cause and effect can propagate through space. This suggests the correct interpretation, which is that for an object compact enough to be a black hole, there is no way for an event at a distance closer than `r` to have an effect on an event far away. There is an invisible, spherical boundary with radius `r`, called the event horizon, and the region within that boundary is cut off from the rest of the universe in terms of cause and effect. If you wanted to explore that region, you could drop into it while wearing a space-suit `-` but it would be a one-way trip, because you could never get back out to report on what you had seen.

In the Newtonian description of a black hole, matter could be lifted out of a black hole, m. Would this be possible with a real-world black hole, which is relativistic rather than Newtonian? No, because the bucket is causally separated from the outside universe. No rope would be strong enough for this job (problem 13, p. 790).

One misleading aspect of the Newtonian analysis is that it encourages us to imagine that a light ray trying to escape from a black hole will slow down, stop, and then fall back in. This can't be right, because we know that any observer who sees a light ray flying by always measures its speed to be `c`. This was true in special relativity, and by the equivalence principle we can be assured that the same is true locally in general relativity. Figure n shows what would really happen.

Although the light rays in figure n don't speed up or slow down, they do experience gravitational Doppler shifts. If a light ray is emitted from just above the event horizon, then it will escape to an infinite distance, but it will suffer an extreme Doppler shift toward low frequencies. A distant observer also has the option of interpreting this as a gravitational time dilation that greatly lowers the frequency of the oscillating electric charges that produced the ray. If the point of emission is made closer and closer to the horizon, the frequency and energy (see p. 782) measured by a distant observer approach zero, making the ray impossible to observe.

Information paradox

Black holes have some disturbing implications for the kind of universe that in the Age of the Enlightenment was imagined to have been set in motion initially and then left to run forever like clockwork.

Newton's laws have built into them the implicit assumption that omniscience is possible, at least in principle. For example, Newton's definition of an inertial frame of reference leads to an infinite regress, as described on p. 801. For Newton this isn't a problem, because in principle an omnisicient observer can know the location of every mass in the universe. In this conception of the cosmos, there are no theoretical limits on human knowledge, only practical ones; if we could gather sufficiently precise data about the state of the universe at one time, and if we could carry out all the calculations to extrapolate into the future, then we could know everything that would ever happen. (See the famous quote by Laplace on p. 18.)

But the existence of event horizons surrounding black holes makes it impossible for any observer to be omniscient; only an observer inside a particular horizon can see what's going on inside that horizon.

Furthermore, a black hole has at its center an infinitely dense point, called a singularity, containing all its mass, and this implies that information can be destroyed and made inaccessible to any observer at all. For example, suppose that astronaut Alice goes on a suicide mission to explore a black hole, free-falling in through the event horizon. She has a certain amount of time to collect data and satisfy her intellectual curiosity, but then she impacts the singularity and is compacted into a mathematical point. Now astronaut Betty decides that she will never be satisfied unless the secrets revealed to Alice are known to her as well `-` and besides, she was Alice's best friend, and she wants to know whether Alice had any last words. Betty can jump through the horizon, but she can never know Alice's last words, nor can any other observer who jumps in after Alice does.

This destruction of information is known as the black hole information paradox, and it's referred to as a paradox because quantum physics (ch. 33-36) has built into its DNA the requirement that information is never lost in this sense.

Formation

Around 1960, as black holes and their strange properties began to be better understood and more widely discussed, many physicists who found these issues distressing comforted themselves with the belief that black holes would never really form from realistic initial conditions, such as the collapse of a massive star. Their skepticism was not entirely unreasonable, since it is usually very hard in astronomy to hit a gravitating target, the reason being that conservation of angular momentum tends to make the projectile swing past. (See problem 13 on p. 417 for a quantitative analysis.) For example, if we wanted to drop a space probe into the sun, we would have to extremely precisely stop its sideways orbital motion so that it would drop almost exactly straight in. Once a star started to collapse, the theory went, and became relatively compact, it would be such a small target that further infalling material would be unlikely to hit it, and the process of collapse would halt. According to this point of view, theorists who had calculated the collapse of a star into a black hole had been oversimplifying by assuming a star that was initially perfectly spherical and nonrotating. Remove the unrealistically perfect symmetry of the initial conditions, and a black hole would never actually form.

But Roger Penrose proved in 1964 that this was wrong. In fact, once an object collapses to a certain density, the Penrose singularity theorem guarantees mathematically that it will collapse further until a singularity is formed, and this singularity is surrounded by an event horizon. Since the brightness of an object like Sagittarius A* is far too low to be explained unless it has an event horizon (the interstellar gas flowing into it would glow due to frictional heating), we can be certain that there really is a singularity at its core.

27.3 Black holes by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.