27.2 The equivalence principle by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
27.2 The equivalence principle
Universality of free-fall
Although light rays and gyroscopes seem to agree that space is curved in a gravitational field, it's always conceivable that we could find something else that would disagree. For example, suppose that there is a new and improved ray called the `"StraightRay"^(TM)`. The StraightRay is like a light ray, but when we construct a triangle out of StraightRays, we always get the Euclidean result for the sum of the angles. We would then have to throw away general relativity's whole idea of describing gravity in terms of curvature. One good way of making a StraightRay would be if we had a supply of some kind of exotic matter `-` call it `"FloatyStuff"^(TM)` `-` that had the ordinary amount of inertia, but was completely unaffected by gravity. We could then shoot a stream of FloatyStuff particles out of a nozzle at nearly the speed of light and make a StraightRay.
Normally when we release a material object in a gravitational field, it experiences a force `mg`, and then by Newton's second law its acceleration is `a=F"/"m=mg"/"m=g`. The `m`'s cancel, which is the reason that everything falls with the same acceleration (in the absence of other forces such as air resistance). The universality of this behavior is what allows us to interpret the gravity geometrically in general relativity. For example, the Gravity Probe B gyroscopes were made out of quartz, but if they had been made out of something else, it wouldn't have mattered. But if we had access to some FloatyStuff, the geometrical picture of gravity would fail, because the "m" that described its susceptibility to gravity would be a different "m" than the one describing its inertia.
The question of the existence or nonexistence of such forms of matter turns out to be related to the question of what kinds of motion are relative. Let's say that alien gangsters land in a flying saucer, kidnap you out of your back yard, konk you on the head, and take you away. When you regain consciousness, you're locked up in a sealed cabin in their spaceship. You pull your keychain out of your pocket and release it, and you observe that it accelerates toward the floor with an acceleration that seems quite a bit slower than what you're used to on earth, perhaps a third of a gee. There are two possible explanations for this. One is that the aliens have taken you to some other planet, maybe Mars, where the strength of gravity is a third of what we have on earth. The other is that your keychain didn't really accelerate at all: you're still inside the flying saucer, which is accelerating at a third of a gee, so that it was really the deck that accelerated up and hit the keys.
There is absolutely no way to tell which of these two scenarios is actually the case `-` unless you happen to have a chunk of FloatyStuff in your other pocket. If you release the FloatyStuff and it hovers above the deck, then you're on another planet and experiencing genuine gravity; your keychain responded to the gravity, but the FloatyStuff didn't. But if you release the FloatyStuff and see it hit the deck, then the flying saucer is accelerating through outer space.
The nonexistence of FloatyStuff in our universe is called the equivalence principle. If the equivalence principle holds, then an acceleration (such as the acceleration of the flying saucer) is always equivalent to a gravitational field, and no observation can ever tell the difference without reference to something external. (And suppose you did have some external reference point `-` how would you know whether it was accelerating?)
Example 2: The artificial horizon
 The pilot of an airplane cannot always easily tell which way is up. The horizon may not be level simply because the ground has an actual slope, and in any case the horizon may not be visible if the weather is foggy. One might imagine that the problem could be solved simply by hanging a pendulum and observing which way it pointed, but by the equivalence principle the pendulum cannot tell the difference between a gravitational field and an acceleration of the aircraft relative to the ground `-` nor can any other accelerometer, such as the pilot's inner ear. For example, when the plane is turning to the right, accelerometers will be tricked into believing that “down” is down and to the left. To get around this problem, airplanes use a device called an artificial horizon, which is essentially a gyroscope. The gyroscope has to be initialized when the plane is known to be oriented in a horizontal plane. No gyroscope is perfect, so over time it will drift. For this reason the instrument also contains an accelerometer, and the gyroscope is always forced into agreement with the accelerometer's average output over the preceding several minutes. If the plane is flown in circles for several minutes, the artificial horizon will be fooled into indicating that the wrong direction is vertical.
The pilot of an airplane cannot always easily tell which way is up. The horizon may not be level simply because the ground has an actual slope, and in any case the horizon may not be visible if the weather is foggy. One might imagine that the problem could be solved simply by hanging a pendulum and observing which way it pointed, but by the equivalence principle the pendulum cannot tell the difference between a gravitational field and an acceleration of the aircraft relative to the ground `-` nor can any other accelerometer, such as the pilot's inner ear. For example, when the plane is turning to the right, accelerometers will be tricked into believing that “down” is down and to the left. To get around this problem, airplanes use a device called an artificial horizon, which is essentially a gyroscope. The gyroscope has to be initialized when the plane is known to be oriented in a horizontal plane. No gyroscope is perfect, so over time it will drift. For this reason the instrument also contains an accelerometer, and the gyroscope is always forced into agreement with the accelerometer's average output over the preceding several minutes. If the plane is flown in circles for several minutes, the artificial horizon will be fooled into indicating that the wrong direction is vertical.
 Gravitational Doppler shifts and time dilation
Gravitational Doppler shifts and time dilation
An interesting application of the equivalence principle is the explanation of gravitational time dilation. As described on p. 652, experiments show that a clock at the top of a mountain runs faster than one down at its foot.
To calculate this effect, we make use of the fact that the gravitational field in the area around the mountain is equivalent to an acceleration. Suppose we're in an elevator accelerating upward with acceleration `a`, and we shoot a ray of light from the floor up toward the ceiling, at height `h`. The time `Deltat` it takes the light ray to get to the ceiling is about `h"/"c`, and by the time the light ray reaches the ceiling, the elevator has sped up by `v=aDeltat=(ah)/c`, so we'll see a red-shift in the ray's frequency. Since `v` is small compared to `c`, we don't need to use the fancy Doppler shift equation from section 24.7; we can just approximate the Doppler shift factor as `1-v"/"capprox1-ah"/"c^2`. By the equivalence principle, we should expect that if a ray of light starts out low down and then rises up through a gravitational field `g`, its frequency will be Doppler shifted by a factor of `1-gh"/"c^2`. This effect was observed in a famous experiment carried out by Pound and Rebka in 1959. Gamma-rays were emitted at the bottom of a 22.5-meter tower at Harvard and detected at the top with the Doppler shift predicted by general relativity. (See problem 4.)
In the mountain-valley experiment, the frequency of the clock in the valley therefore appears to be running too slowly by a factor of `1-gh"/"c^2` when it is compared via radio with the clock at the top of the mountain. We conclude that time runs more slowly when one is lower down in a gravitational field, and the slow-down factor between two points is given by `1-gh"/"c^2`, where `h` is the difference in height.
We have built up a picture of light rays interacting with gravity. To confirm that this make sense, recall that we have already observed on p. 693 and in problem 12 on p. 789 that light has momentum. The equivalence principle says that whatever has inertia must also participate in gravitational interactions. Therefore light waves must have weight, and must lose energy when they rise through a gravitational field(cf. p. 782).
Local flatness
The noneuclidean nature of spacetime produces effects that grow in proportion to the area of the region being considered. Interpreting such effects as evidence of curvature, we see that this connects naturally to the idea that curvature is undetectable from close up. For example, the curvature of the earth's surface is not normally noticeable to us in everyday life. Locally, the earth's surface is flat, and the same is true for spacetime.
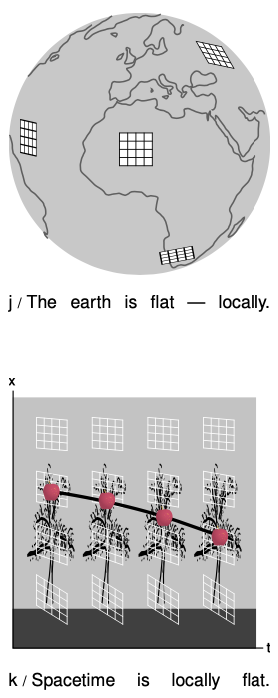 Local flatness turns out to be another way of stating the equivalence principle. In a variation on the alien-abduction story, suppose that you regain consciousness aboard the flying saucer and find yourself weightless. If the equivalence principle holds, then you have no way of determining from local observations, inside the saucer, whether you are actually weightless in deep space, or simply free-falling in apparent weightlessness, like the astronauts aboard the International Space Station. That means that locally, we can always adopt a free-falling frame of reference in which there is no gravitational field at all. If there is no gravity, then special relativity is valid, and we can treat our local region of spacetime as being approximately flat.
Local flatness turns out to be another way of stating the equivalence principle. In a variation on the alien-abduction story, suppose that you regain consciousness aboard the flying saucer and find yourself weightless. If the equivalence principle holds, then you have no way of determining from local observations, inside the saucer, whether you are actually weightless in deep space, or simply free-falling in apparent weightlessness, like the astronauts aboard the International Space Station. That means that locally, we can always adopt a free-falling frame of reference in which there is no gravitational field at all. If there is no gravity, then special relativity is valid, and we can treat our local region of spacetime as being approximately flat.
In figure k, an apple falls out of a tree. Its path is a “straight” line in spacetime, in the same sense that the equator is a “straight” line on the earth's surface.
Inertial frames
In Newtonian mechanics, we have a distinction between inertial and noninertial frames of reference. An inertial frame according to Newton is one that has a constant velocity vector relative to the stars. But what if the stars themselves are accelerating due to a gravitational force from the rest of the galaxy? We could then take the galaxy's center of mass as defining an inertial frame, but what if something else is acting on the galaxy?

If we had some FloatyStuff, we could resolve the whole question. FloatyStuff isn't affected by gravity, so if we release a sample of it in mid-air, it will continue on a trajectory that defines a perfect Newtonian inertial frame. (We'd better have it on a tether, because otherwise the earth's rotation will carry the earth out from under it.) But if the equivalence principle holds, then Newton's definition of an inertial frame is fundamentally flawed.
There is a different definition of an inertial frame that works better in relativity. A Newtonian inertial frame was defined by an object that isn't subject to any forces, gravitational or otherwise. In general relativity, we instead define an inertial frame using an object that that isn't influenced by anything other than gravity. By this definition, a free-falling rock defines an inertial frame, but this book sitting on your desk does not.
27.2 The equivalence principle by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.