27.1 Our universe isn't Euclidean by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
27.1 Our universe isn't Euclidean
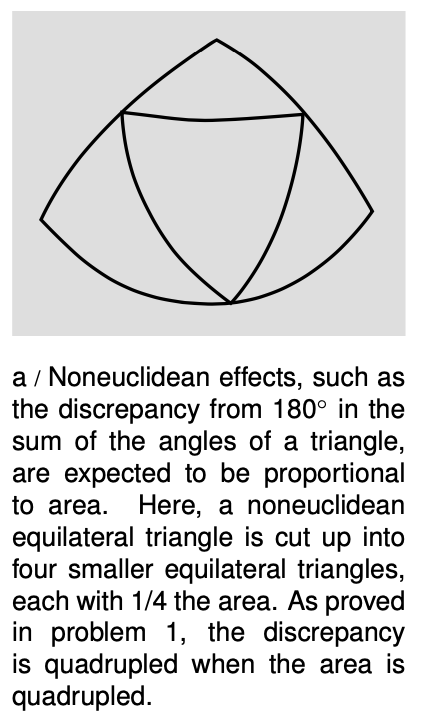 Euclid proved thousands of years ago that the angles in a triangle add up to `180°`. But what does it really mean to “prove” this? Euclid proved it based on certain assumptions (his five postulates), listed in the margin of this page. But how do we know that the postulates are true?
Euclid proved thousands of years ago that the angles in a triangle add up to `180°`. But what does it really mean to “prove” this? Euclid proved it based on certain assumptions (his five postulates), listed in the margin of this page. But how do we know that the postulates are true?
Only by observation can we tell whether any of Euclid's statements are correct characterizations of how space actually behaves in our universe. If we draw a triangle on paper with a ruler and measure its angles with a protractor, we will quickly verify to pretty good precision that the sum is close to `180°`. But of course we already knew that space was at least approximately Euclidean. If there had been any gross error in Euclidean geometry, it would have been detected in Euclid's own lifetime. The correspondence principle tells us that if there is going to be any deviation from Euclidean geometry, it must be small under ordinary conditions.
To improve the precision of the experiment, we need to make sure that our ruler is very straight. One way to check would be to sight along it by eye, which amounts to comparing its straightness to that of a ray of light. For that matter, we might as well throw the physical ruler in the trash and construct our triangle out of three laser beams. To avoid effects from the air we should do the experiment in outer space. Doing it in space also has the advantage of allowing us to make the triangle very large; as shown in figure a, the discrepancy from `180°` is expected to be proportional to the area of the triangle.
 But we already know that light rays are bent by gravity. We expect it based on `E=mc^2`, which tells us that the energy of a light ray is equivalent to a certain amount of mass, and furthermore it has been verified experimentally by the deflection of starlight by the sun (example 8, p. 777). We therefore know that our universe is noneuclidean, and we gain the further insight that the level of deviation from Euclidean behavior depends on gravity.
But we already know that light rays are bent by gravity. We expect it based on `E=mc^2`, which tells us that the energy of a light ray is equivalent to a certain amount of mass, and furthermore it has been verified experimentally by the deflection of starlight by the sun (example 8, p. 777). We therefore know that our universe is noneuclidean, and we gain the further insight that the level of deviation from Euclidean behavior depends on gravity.
Since the noneuclidean effects are bigger when the system being studied is larger, we expect them to be especially important in the study of cosmology, where the distance scales are very large.
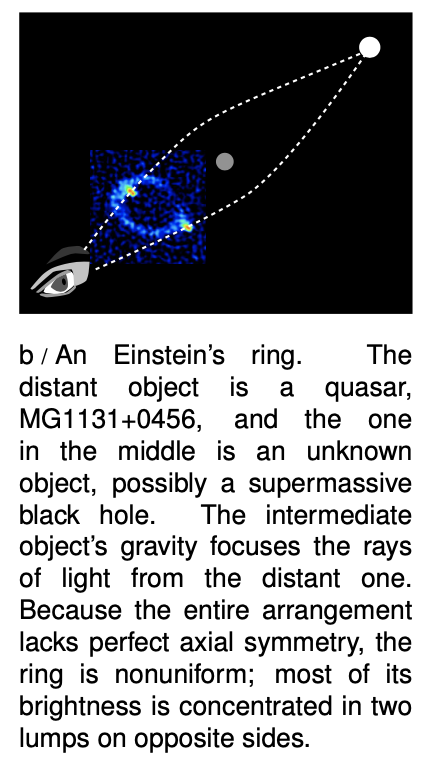
Example 1: Einstein's ring
An Einstein's ring, figure b, is formed when there is a chance alignment of a distant source with a closer gravitating body. This type of gravitational lensing is direct evidence for the noneuclidean nature of space. The two light rays are lines, and they violate Euclid's first postulate, that two points determine a line.
One could protest that effects like these are just an imperfection of the light rays as physical models of straight lines. Maybe the noneuclidean effects would go away if we used something better and straighter than a light ray. But we don't know of anything straighter than a light ray. Furthermore, we observe that all measuring devices, not just optical ones, report the same noneuclidean behavior.
Curvature
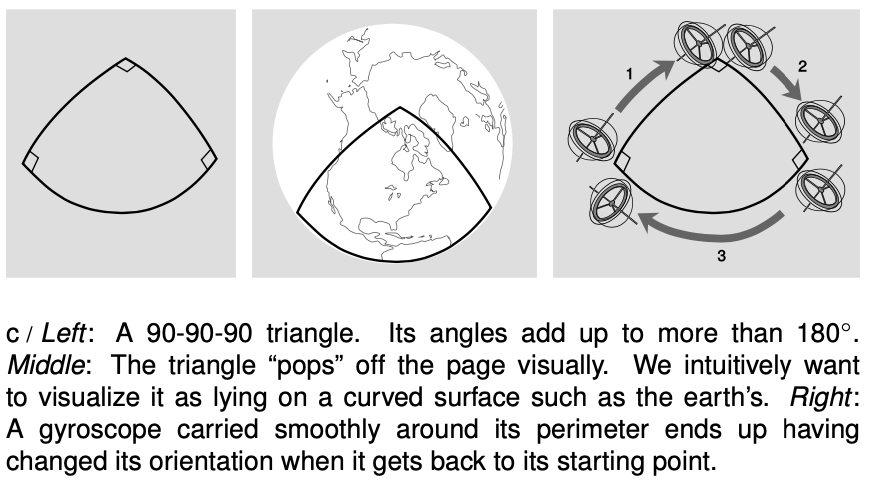
An example of such a non-optical measurement is the Gravity Probe B satellite, figure d, which was launched into a polar orbit in 2004 and operated until 2010. The probe carried four gyroscopes made of quartz, which were the most perfect spheres ever manufactured, varying from sphericity by no more than about 40 atoms. Each gyroscope floated weightlessly in a vacuum, so that its rotation was perfectly steady. After 5000 orbits, the gyroscopes had reoriented themselves by about `2×10^(-3)°` relative to the distant stars. This effect cannot be explained by Newtonian physics, since no torques acted on them. It was, however, exactly as predicted by Einstein's theory of general relativity. It becomes easier to see why such an effect would be expected due to the noneuclidean nature of space if we characterize euclidean geometry as the geometry of a flat plane as opposed to a curved one. On a curved surface like a sphere, figure c, Euclid's fifth postulate fails, and it's not hard to see that we can get triangles for which the sum of the angles is not `180°`. By transporting a gyroscope all the way around the edges of such a triangle and back to its starting point, we change its orientation.
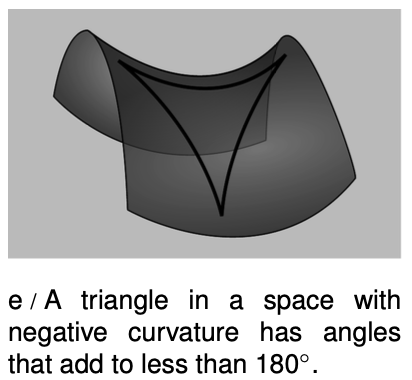
The triangle in figure c has angles that add up to more than `180°`. This type of curvature is referred to as positive. It is 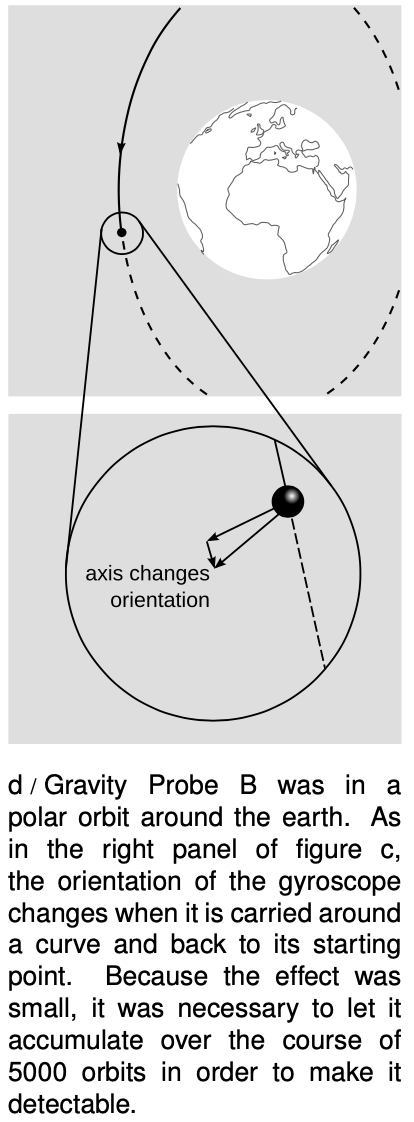 also possible to have negative curvature, as in figure e.
also possible to have negative curvature, as in figure e.
In general relativity, curvature isn't just something caused by gravity. Gravity is curvature, and the curvature involves both space and time, as may become clearer once you get to figure k. Thus the distinction between special and general relativity is that general relativity handles curved space time, while special relativity is restricted to the case where space time is flat.
Curvature doesn't require higher dimensions
Although we often visualize curvature by imagining embedding a two-dimensional surface in a three-dimensional space, that's just an aid in visualization. There is no evidence for any additional dimensions, nor is it necessary to hypothesize them in order to let space time be curved as described in general relativity.
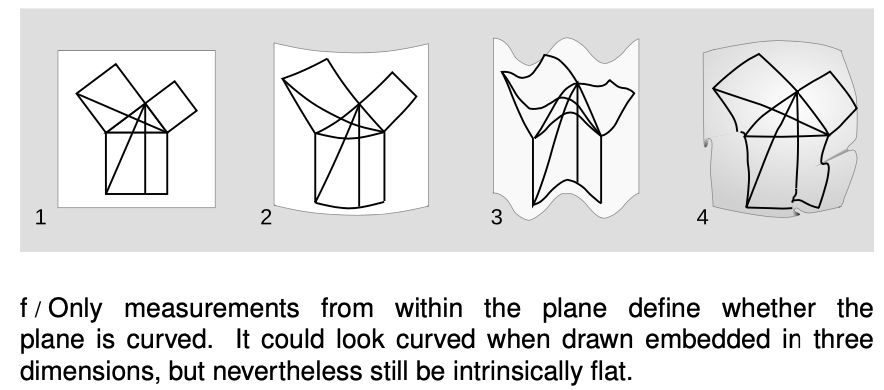
Put yourself in the shoes of a two-dimensional being living in a two-dimensional space. Euclid's postulates all refer to constructions that can be performed using a compass and an unmarked straightedge. If this being can physically verify them all as descriptions of the space she inhabits, then she knows that her space is Euclidean, and that propositions such as the Pythagorean theorem are physically valid in her universe. But the diagram in f/1 illustrating the proof of the Pythagorean theorem in Euclid's Elements (proposition I.47) is equally valid if the page is rolled onto a cylinder, 2, or formed into a wavy corrugated shape, 3. These types of curvature, which can be achieved without tearing or crumpling the surface, are not real to her. They are simply side-effects of visualizing her two-dimensional universe as if it were embedded in a hypothetical third dimension `-` which doesn't exist in any sense that is empirically verifiable to her. Of the curved surfaces in figure f, only the sphere, 4, has curvature that she can measure; the diagram can't be plastered onto the sphere without folding or cutting and pasting.
So the observation of curvature doesn't imply the existence of extra dimensions, nor does embedding a space in a higher-dimensional one so that it looks curvy always mean that there will be any curvature detectable from within the lower-dimensional space.
27.1 Our universe isn't Euclidean by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.