26.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
alpha particle — a form of radioactivity consisting of helium nuclei
beta particle — a form of radioactivity consisting of electrons
gamma ray — a form of radioactivity consisting of a very high-frequency form of light
proton — a positively charged particle, one of the types that nuclei are made of
neutron — an uncharged particle, the other types that nuclei are made of
isotope — one of the possible varieties of atoms of a given element, having a certain number of neutrons
atomic number — the number of protons in an atom's nucleus; determines what element it is
atomic mass — the mass of an atom
mass number — the number of protons plus the number of neutrons in a nucleus; approximately proportional to its atomic mass
strong nuclear force — the force that holds nuclei together against electrical repulsion
weak nuclear force — the force responsible for beta decay
beta decay — the radioactive decay of a nucleus via the reaction `n->p+e^(-)+barnu` or `p->n+e^++nu`; so called because an electron or antielectron is also known as a beta particle
alpha decay — the radioactive decay of a nucleus via emission of an alpha particle
fission — the radioactive decay of a nucleus by splitting into two parts
fusion — a nuclear reaction in which two nuclei stick together to form one bigger nucleus
`muSv` — a unit for measuring a person's exposure to radioactivity
Notation
`e^-` — an electron
`e^+` — an antielectron; just like an electron, but with positive charge
n — a neutron
p — a proton
`nu` — a neutrino
`barnu` — an antineutrino
`mathcalE` — mass-energy
Other Notation
`Z` — atomic number (number of protons in a nucleus)
`N` — number of neutrons in a nucleus
`A` — mass number `(N+Z)`
Summary
Quantization of charge: Millikan's oil drop experiment showed that the total charge of an object could only be an integer multiple of a basic unit of charge `(e)`. This supported the idea the the “flow” of electrical charge was the motion of tiny particles rather than the motion of some sort of mysterious electrical fluid.
Einstein's analysis of Brownian motion was the first definitive proof of the existence of atoms. Thomson's experiments with vacuum tubes demonstrated the existence of a new type of microscopic particle with a very small ratio of mass to charge. Thomson correctly interpreted these as building blocks of matter even smaller than atoms: the first discovery of subatomic particles. These particles are called electrons.
The above experimental evidence led to the first useful model of the interior structure of atoms, called the raisin cookie model. In the raisin cookie model, an atom consists of a relatively large, massive, positively charged sphere with a certain number of negatively charged electrons embedded in it.
Rutherford and Marsden observed that some alpha particles from a beam striking a thin gold foil came back at angles up to 180 degrees. This could not be explained in the then-favored raisin-cookie model of the atom, and led to the adoption of the planetary model of the atom, in which the electrons orbit a tiny, positively-charged nucleus. Further experiments showed that the nucleus itself was a cluster of positively-charged protons and uncharged neutrons.
Radioactive nuclei are those that can release energy. The most common types of radioactivity are alpha decay (the emission of a helium nucleus), beta decay (the transformation of a neutron into a proton or vice-versa), and gamma decay (the emission of a type of very-high-frequency light). Stars are powered by nuclear fusion reactions, in which two light nuclei collide and form a bigger nucleus, with the release of energy.
Human exposure to ionizing radiation is measured in units of microsieverts `(muSv)`. The typical person is exposed to about 2000 `muSv` worth of natural background radiation per year.
Exploring further
The First Three Minutes, Steven Weinberg.
This book describes the first three minutes of the universe's existence.
Homework Problems
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. Use the nutritional information on some packaged food to make an order-of-magnitude estimate of the amount of chemical energy stored in one atom of food, in units of joules. Assume that a typical atom has a mass of `10^(-26)` kg. This constitutes a rough estimate of the amounts of energy there are on the atomic scale. [See chapter 1 for help on how to do order-of-magnitude estimates. Note that a nutritional “calorie” is really a kilocalorie.] `sqrt`
2. The nuclear process of beta decay by electron capture is described parenthetically on p. 761. The reaction is `p+e^-->n+nu`. (a) Show that charge is conserved in this reaction.
(b) Explain why electron capture doesn't occur in hydrogen atoms. (If it did, matter wouldn't exist!)
3. 234Pu decays either by electron decay or by alpha decay. (A given 234Pu nucleus may do either one; it's random.) What are the isotopes created as products of these two modes of decay?
4. (a) Recall that the gravitational energy of two gravitationally interacting spheres is given by `PE=(-Gm_1m_2)/r` where `r` is the center-to-center distance. What would be the analogous equation for two electrically interacting spheres? Justify your choice of a plus or minus sign on physical grounds, considering attraction and repulsion.
(b) Use this expression to estimate the energy required to pull apart a raisin-cookie atom of the one-electron type, assuming a radius of `10^(-10)` m. `sqrt`
(c) Compare this with the result of problem 1.
5. A neon light consists of a long glass tube full of neon, with metal caps on the ends. Positive charge is placed on one end of the tube, negative on the other. The electric forces generated can be strong enough to strip electrons off of a certain number of neon atoms. Assume for simplicity that only one electron is ever stripped off of any neon atom. When an electron is stripped off of an atom, both the electron and the neon atom (now an ion) have electric charge, and they are accelerated by the forces exerted by the charged ends of the tube. (They do not feel any significant forces from the other ions and electrons within the tube, because only a tiny minority of neon atoms ever gets ionized.) Light is finally produced when ions are reunited with electrons. Give a numerical comparison of the magnitudes and directions of the accelerations of the electrons and ions. [You may need some data from page 1028.] `sqrt`
6. If you put two hydrogen atoms near each other, they will feel an attractive force, and they will pull together to form a molecule. (Molecules consisting of two hydrogen atoms are the normal form of hydrogen gas.) How is this possible, since each is electrically neutral? Shouldn't the attractive and repulsive forces all cancel out exactly? Use the raisin cookie model. (Students who have taken chemistry often try to use fancier models to explain this, but if you can't explain it using a simple model, you probably don't understand the fancy model as well as you thought you did!) It's not so easy to prove that the force should actually be attractive rather than repulsive, so just concentrate on explaining why it doesn't necessarily have to vanish completely.
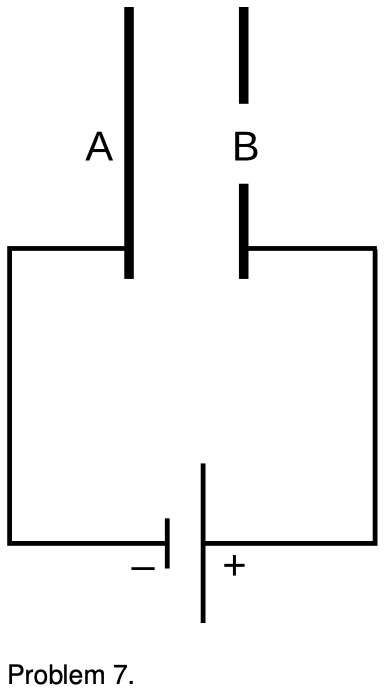 7. The figure shows a simplified diagram of an electron gun such as the one used in an old-fashioned TV tube. Electrons that spontaneously emerge from the negative electrode (cathode) are then accelerated to the positive electrode, which has a hole in it. (Once they emerge through the hole, they will slow down. However, if the two electrodes are fairly close together, this slowing down is a small effect, because the attractive and repulsive forces experienced by the electron tend to cancel.) (a) If the voltage difference between the electrodes is `DeltaV`, what is the velocity of an electron as it emerges at B? (Assume its initial velocity, at A, is negligible.) (b) Evaluate your expression numerically for the case where `DeltaV=10 kV`, and compare to the speed of light.
7. The figure shows a simplified diagram of an electron gun such as the one used in an old-fashioned TV tube. Electrons that spontaneously emerge from the negative electrode (cathode) are then accelerated to the positive electrode, which has a hole in it. (Once they emerge through the hole, they will slow down. However, if the two electrodes are fairly close together, this slowing down is a small effect, because the attractive and repulsive forces experienced by the electron tend to cancel.) (a) If the voltage difference between the electrodes is `DeltaV`, what is the velocity of an electron as it emerges at B? (Assume its initial velocity, at A, is negligible.) (b) Evaluate your expression numerically for the case where `DeltaV=10 kV`, and compare to the speed of light.
8. The figure shows a simplified diagram of a device called a tandem accelerator, used for accelerating beams of ions up to speeds on the order of 1-10% of the speed of light. (Since these velocities are not too big compared to `c`, you can use nonrelativistic physics throughout this problem.) The nuclei of these ions collide with the nuclei of atoms in a target, producing nuclear reactions for experiments studying the structure of nuclei. The outer shell of the accelerator is a conductor at zero voltage (i.e., the same voltage as the Earth). The electrode at the center, known as the “terminal,” is at a high positive voltage, perhaps millions of volts. Negative ions with a charge of `-1` unit (i.e., atoms with one extra electron) are produced offstage on the right, typically by chemical reactions with cesium, which is a chemical element that has a strong tendency to give away electrons. Relatively weak electric and magnetic forces are used to transport these `-1` ions into the accelerator, where they are attracted to the terminal. Although the center of the terminal has a hole in it to let the ions pass through, there is a very thin carbon foil there that they must physically penetrate. Passing through the foil strips off some number of electrons, changing the atom into a positive ion, with a charge of `+n` times the fundamental charge. Now that the atom is positive, it is repelled by the terminal, and accelerates some more on its way out of the accelerator. (a) Find the velocity, `v`, of the emerging beam of positive ions, in terms of `n`, their mass `m`, the terminal voltage `V`, and fundamental constants. Neglect the small change in mass caused by the loss of electrons in the stripper foil. `sqrt`
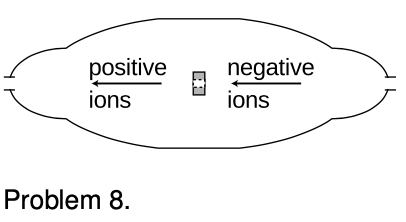 (b) To fuse protons with protons, a minimum beam velocity of about 11% of the speed of light is required. What terminal voltage would be needed in this case? `sqrt`
(b) To fuse protons with protons, a minimum beam velocity of about 11% of the speed of light is required. What terminal voltage would be needed in this case? `sqrt`
9. In example 4 on page 663, I remarked that accelerating a macroscopic (i.e., not microscopic) object to close to the speed of light would require an unreasonable amount of energy. Suppose that the starship Enterprise from Star Trek has a mass of `8.0×10^7` kg, about the same as the Queen Elizabeth 2. Compute the kinetic energy it would have to have if it was moving at half the speed of light. Compare with the total energy content of the world's nuclear arsenals, which is about `10^21` J. `sqrt`
10. (a) A free neutron (as opposed to a neutron bound into an atomic nucleus) is unstable, and undergoes beta decay (which you may want to review). The masses of the particles involved are as follows:
| neutron | 1.67495×1027 kg |
| proton | `1.67265×10-27 kg` |
| electron | `0.00091×10-27 kg` |
| antineutrino | `< 10-35 kg` |
Find the energy released in the decay of a free neutron. `sqrt`
(b) Neutrons and protons make up essentially all of the mass of the ordinary matter around us. We observe that the universe around us has no free neutrons, but lots of free protons (the nuclei of hydrogen, which is the element that 90% of the universe is made of). We find neutrons only inside nuclei along with other neutrons and protons, not on their own.
If there are processes that can convert neutrons into protons, we might imagine that there could also be proton-to-neutron conversions, and indeed such a process does occur sometimes in nuclei that contain both neutrons and protons: a proton can decay into a neutron, a positron, and a neutrino. A positron is a particle with the same properties as an electron, except that its electrical charge is positive. A neutrino, like an antineutrino, has negligible mass.
Although such a process can occur within a nucleus, explain why it cannot happen to a free proton. (If it could, hydrogen would be radioactive, and you wouldn't exist!
11.(a) Find a relativistic equation for the velocity of an object in terms of its mass and momentum (eliminating `gamma`). `sqrt`
(b) Show that your result is approximately the same as the nonrelativistic value, `p"/"m`, at low velocities.
(c) Show that very large momenta result in speeds close to the speed of light. `***`
12. An object moving at a speed very close to the speed of light is referred to as ultrarelativistic. Ordinarily (luckily) the only ultrarelativistic objects in our universe are subatomic particles, such as cosmic rays or particles that have been accelerated in a particle accelerator.
(a) What kind of number is `gamma` for an ultrarelativistic particle?
(b) Repeat example 12 on page 780, but instead of very low, nonrelativistic speeds, consider ultrarelativistic speeds.
(c) Find an equation for the ratio `mathcalE"/"p`. The speed may be relativistic, but don't assume that it's ultrarelativistic. `sqrt`
(d) Simplify your answer to part c for the case where the speed is ultrarelativistic. `sqrt`
(e) We can think of a beam of light as an ultrarelativistic object --- it certainly moves at a speed that's sufficiently close to the speed of light! Suppose you turn on a one-watt flashlight, leave it on for one second, and then turn it off. Compute the momentum of the recoiling flashlight, in units of `kg*m"/"s`. (Cf. p. 693.) `sqrt`
(f) Discuss how your answer in part e relates to the correspondence principle.
13. As discussed in chapter 19, the speed at which a disturbance travels along a string under tension is given by, where `?` is the mass per unit length, and `T` is the tension.
(a) Suppose a string has a density `rho`, and a cross-sectional area `A`. Find an expression for the maximum tension that could possibly exist in the string without producing `v>c`, which is impossible according to relativity. Express your answer in terms of `rho`, `A`, and `c`. The interpretation is that relativity puts a limit on how strong any material can be.`sqrt`
(b) Every substance has a tensile strength, defined as the force per unit area required to break it by pulling it apart. The tensile strength is measured in units of `N"/"m^2`, which is the same as the pascal (Pa), the mks unit of pressure. Make a numerical estimate of the maximum tensile strength allowed by relativity in the case where the rope is made out of ordinary matter, with a density on the same order of magnitude as that of water. (For comparison, kevlar has a tensile strength of about `4×10^9 Pa`, and there is speculation that fibers made from carbon nanotubes could have values as high as `6×10^10Pa`.) `sqrt`
(c) A black hole is a star that has collapsed and become very dense, so that its gravity is too strong for anything ever to escape from it. For instance, the escape velocity from a black hole is greater than `c`, so a projectile can't be shot out of it. Many people, when they hear this description of a black hole in terms of an escape velocity greater than `c`, wonder why it still wouldn't be possible to extract an object from a black hole by other means than launching it out as a projectile. For example, suppose we lower an astronaut into a black hole on a rope, and then pull him back out again. Why might this not work?
14. (a) A charged particle is surrounded by a uniform electric field. Starting from rest, it is accelerated by the field to speed `v` after traveling a distance `d`. Now it is allowed to continue for a further distance `3d`, for a total displacement from the start of `4d`. What speed will it reach, assuming classical physics?
(b) Find the relativistic result for the case of `v=c"/"2`.
15. Problem 15 on p. 382 (with the solution given in the back of the book) demonstrates that in Newtonian mechanics, conservation of momentum is the necessary and sufficient condition if conservation of energy is to hold in all frames of reference. The purpose of this problem is to generalize that idea to relativity (in one dimension).
Let a system contain two interacting particles, each with unit mass. Then if energy is conserved in a particular frame, we must have `gamma_1+gamma_2=gamma_1'+gamma_2'`, where the primes indicate the quantities after interaction. Suppose that we now change to a new frame, in motion relative to the first one at a velocity `epsilon` that is much less than 1 (in units where `c=1`). The velocities all change according to the result of problem 21 on p. 705. Show that energy is conserved in the new frame if and only if momentum is conserved.
Hints: (1) Since `epsilon` is small, you can take `1"/"(1+epsilon)approx1-epsilon`. (2) Rather than directly using the result of problem 21, it is easier to eliminate the velocities in favor of the corresponding Doppler-shift factors `D`, which simply multiply when the velocities are combined. (3) The identity `vgamma=(1"/"D-D)"/"2` is handy here. `***`
Exercise 26A: Sports in Slowlightland
In Slowlightland, the speed of light is 20 mi/hr = 32 km/hr = 9 m/s. Think of an example of how relativistic effects would work in sports. Things can get very complex very quickly, so try to think of a simple example that focuses on just one of the following effects:
- relativistic momentum
- relativistic kinetic energy
- relativistic addition of velocities (See problem 21, with the answer given on p. 1008.)
- time dilation and length contraction
- Doppler shifts of light (See section 24.7.)
- equivalence of mass and energy
- time it takes for light to get to an athlete's eye
- deflection of light rays by gravity
Exercise 26B: Nuclear decay
1. Consulting a periodic table, find the `N`, `Z`, and `A` of the following:
| `N` | `Z` | `A` | |
| 4He | |||
| 244Pu |
2. Consider the following five decay processes:
- `alpha` decay
- `gamma` decay
- `p->n+e^++nu` (`beta^+` decay)
- `n->p+e^-+barnu` (`beta^-` decay)
- `p+e^-->n+nu` (electron capture)
What would be the action of each of these on the chart of the nuclei? The `***` represents the original nucleus.
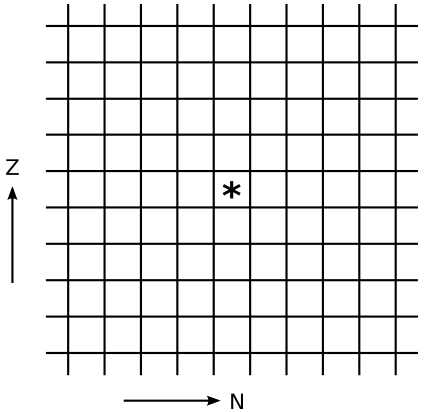
3. (a) Suppose that 244Pu undergoes perfectly symmetric fission, and also emits two neutrons. Find the slope isotope.
(b) Is the daughter stable, or is it neutron-rich or -poor relative to the line of stability? (To estimate what's stable you can use a large chart of the nuclei, or, if you don't have one handy, consult a periodic table and use the average atomic mass as an approximation of the stable value of `A`.)
(c) Consulting the chart of nuclei, explain why it turns out this way.
(d) If the daughter is unstable, which process from question #2 would you expect it to decay by?
Exercise 26C: Misconceptions about relativity
The following is a list of common misconceptions about relativity. The class will be split up into random groups, and each group will cooperate on developing an explanation of the misconception, and then the groups will present their explanations to the class. There may be multiple rounds, with students assigned to different randomly chosen groups in successive rounds.
- How can light have momentum if it has zero mass?
- What does the world look like in a frame of reference moving at `c`?
- Alice observes Betty coming toward her from the left at `c"/"2`, and Carol from the right at `c"/"2`. Therefore Betty is moving at the speed of light relative to Carol.
- Are relativistic effects such as length contraction and time dilation real, or do they just seem to be that way?
- Special relativity only matters if you've moving close to the speed of light.
- Special relativity says that everything is relative.
- There is a common misconception that relativistic length contraction is what we would actually see. Refute this by drawing a spacetime diagram for an object approaching an observer, and tracing rays of light emitted from the object's front and back that both reach the observer's eye at the same time.
- When you travel close to the speed of light, your time slows down.
- Is a light wave's wavelength relativistically length contracted by a factor of gamma?
- Accelerate a baseball to ultrarelativistic speeds. Does it become a black hole?
- Where did the Big Bang happen?
- The universe can't be infinite in size, because it's only had a finite amount of time to expand from the point where the Big Bang happened.
26.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.