26.5 Relativistic mass and energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
26.5 Relativistic mass and energy
The radioactive decay processes described in this chapter do not conserve mass. For example, you're probably reading this in a building that has smoke detectors containing the isotope 241Am, an alpha emitter. The decay products are a helium atom plus an atom of 237Np. In units of `10^(-27) kg, the masses involved are:
| 241Am | 400.28421 |
| 237Np | 393.62768 |
| 4He | 6.64647 |
The final state has a total mass of `400.27415` of these units, meaning a loss of `0.01006`. This is an example of Einstein's famous `E=mc^2` at work: some mass has been converted into energy. In fact this type of mass-energy conversion is not just a property of nuclear decay. It is an example of a much wider set of phenomena in relativity. Let's see how quantities like mass, force, momentum, and energy behave relativistically.
Momentum
Consider the following scheme for traveling faster than the speed of light. The basic idea can be demonstrated by dropping a ping-pong ball and a baseball stacked on top of each other like a snowman. They separate slightly in mid-air, and the baseball therefore has time to hit the floor and rebound before it collides with the ping-pong ball, which is still on the way down. The result is a surprise if you haven't seen it before: the ping-pong ball flies off at high speed and hits the ceiling! A similar fact is known to people who investigate the scenes of accidents involving pedestrians. If a car moving at `90` kilometers per hour hits a pedestrian, the pedestrian flies off at nearly double that speed, `180` kilometers per hour. Now suppose the car was moving at `90` percent of the speed of light. Would the pedestrian fly off at `180%` of `c`?
To see why not, we have to back up a little and think about where this speed-doubling result comes from. For any collision, there is a special frame of reference, the center-of-mass frame, in which the two colliding objects approach each other, collide, and rebound with their velocities reversed. In the center-of-mass frame, the total momentum of the objects is zero both before and after the collision.
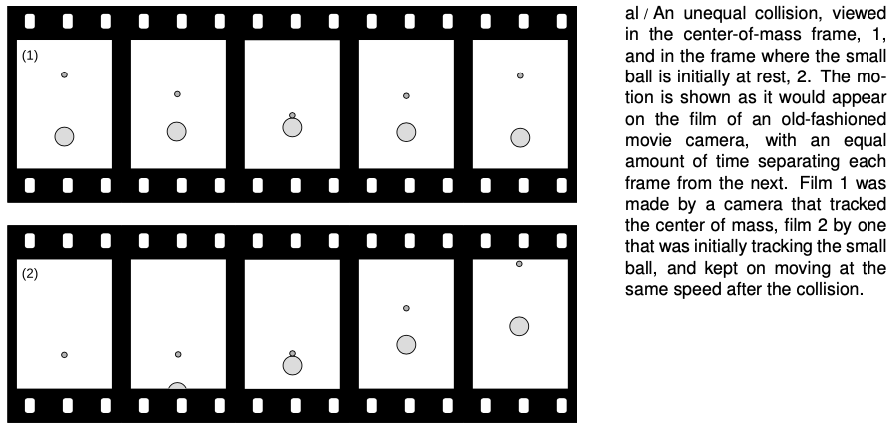
Figure al/1 shows such a frame of reference for objects of very unequal mass. Before the collision, the large ball is moving relatively slowly toward the top of the page, but because of its greater mass, its momentum cancels the momentum of the smaller ball, which is moving rapidly in the opposite direction. The total momentum is zero. After the collision, the two balls just reverse their directions of motion. We know that this is the right result for the outcome of the collision because it conserves both momentum and kinetic energy, and everything not forbidden is compulsory, i.e., in any experiment, there is only one possible outcome, which is the one that obeys all the conservation laws.
self-check:
How do we know that momentum and kinetic energy are conserved in figure al/1?
(answer in the back of the PDF version of the book)
Let's make up some numbers as an example. Say the small ball is `1` kg, the big one `6` kg. In frame 1, let's make the velocities as follows:

Figure al/2 shows the same collision in a frame of reference where the small ball was initially at rest. To find all the velocities in this frame, we just add 0.6 to all the ones in the previous table.

In this frame, as expected, the small ball flies off with a velocity, 1.2, that is almost twice the initial velocity of the big ball, 0.7. In this example the ratio of the two balls' masses was 6, but if the ratio of the masses is made larger and larger, the ratio of the velocities gets closer and closer to 2.
If all those velocities were in meters per second, then that's exactly what would happen. But what if all these velocities were in units of the speed of light? Now it's no longer a good approximation just to add velocities. We need to combine them according to the relativistic rules. For instance, in problem 1 on p. 700 you showed that combining a velocity of 0.6 times the speed of light with another velocity of 0.6 results in 0.88, not 1.2. The results are very different:

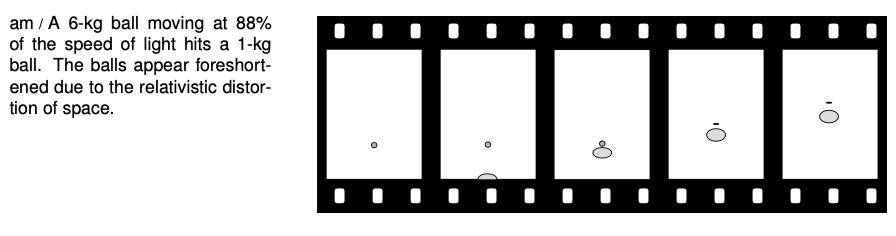
We can interpret this as follows. Figure al/1 is one in which the big ball is moving fairly slowly. This is very nearly the way the scene would be seen by an ant standing on the big ball. According to an observer in frame am, however, both balls are moving at nearly the speed of light after the collision. Because of this, the balls appear foreshortened, but the distance between the two balls is also shortened. To this observer, it seems that the small ball isn't pulling away from the big ball very fast.
Now here's what's interesting about all this. The outcome shown in figure al/2 was supposed to be the only one possible, the only one that satisfied both conservation of energy and conservation of momentum. So how can the different result shown in figure am be possible? The answer is that relativistically, momentum must not equal `mv`. The old, familiar definition is only an approximation that's valid at low speeds. If we observe the behavior of the small ball in figure am, it looks as though it somehow had some extra inertia. It's as though a football player tried to knock another player down without realizing that the other guy had a three-hundred-pound bag full of lead shot hidden under his uniform --- he just doesn't seem to react to the collision as much as he should. This extra inertia is described8 by redefining momentum as
At very low velocities, `gamma` is close to 1, and the result is very nearly `mv`, as demanded by the correspondence principle. But at very high velocities, `gamma` gets very big --- the small ball in figure am has a `gamma` of 2.1, and therefore has more than double the inertia that we would expect nonrelativistically.
This also explains the answer to another paradox often posed by beginners at relativity. Suppose you keep on applying a steady force to an object that's already moving at `0.9999c`. Why doesn't it just keep on speeding up past `c`? The answer is that force is the rate of change of momentum. At `0.9999c`, an object already has a `gamma` of 71, and therefore has already sucked up 71 times the momentum you'd expect at that speed. As its velocity gets closer and closer to `c`, its `gamma` approaches infinity. To move at `c`, it would need an infinite momentum, which could only be caused by an infinite force.
Example 7: Push as hard as you like ...
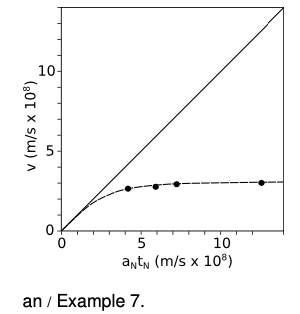 We don't have to depend on our imaginations to see what would happen if we kept on applying a force to an object indefinitely and tried to accelerate it past `c`. A nice experiment of this type was done by Bertozzi in 1964. In this experiment, electrons were accelerated by an electric field `E` through a distance `?_1`. Applying Newton's laws gives Newtonian predictions `a_N` for the acceleration and `t_N` for the time required.6
We don't have to depend on our imaginations to see what would happen if we kept on applying a force to an object indefinitely and tried to accelerate it past `c`. A nice experiment of this type was done by Bertozzi in 1964. In this experiment, electrons were accelerated by an electric field `E` through a distance `?_1`. Applying Newton's laws gives Newtonian predictions `a_N` for the acceleration and `t_N` for the time required.6
The electrons were then allowed to fly down a pipe for a further distance `?_2=8.4 m` without being acted on by any force. The time of flight `t_2` for this second distance was used to find the final velocity `v=?_2"/"t_2` to which they had actually been accelerated.
Figure an shows the results.7 According to Newton, an acceleration `a_N` acting for a time `t_N` should produce a final velocity `a_Nt_N`. The solid line in the graph shows the prediction of Newton's laws, which is that a constant force exerted steadily over time will produce a velocity that rises linearly and without limit.
The experimental data, shown as black dots, clearly tell a different story. The velocity never goes above a certain maximum value, which we identify as `c`. The dashed line shows the predictions of special relativity, which are in good agreement with the experimental results.
Equivalence of mass and energy
Now we're ready to see why mass and energy must be equivalent as claimed in the famous `E=mc^2`. So far we've only considered collisions in which none of the kinetic energy is converted into any other form of energy, such as heat or sound. Let's consider what happens if a blob of putty moving at velocity `v` hits another blob that is initially at rest, sticking to it. The nonrelativistic result is that to obey conservation of momentum the two blobs must fly off together at `v"/"2`. Half of the initial kinetic energy has been converted to heat.9
Relativistically, however, an interesting thing happens. A hot object has more momentum than a cold object! This is because the relativistically correct expression for momentum is `mgammav`, and the more rapidly moving atoms in the hot object have higher values of `gamma`. In our collision, the final combined blob must therefore be moving a little more slowly than the expected `v"/"2`, since otherwise the final momentum would have been a little greater than the initial momentum. To an observer who believes in conservation of momentum and knows only about the overall motion of the objects and not about their heat content, the low velocity after the collision would seem to be the result of a magical change in the mass, as if the mass of two combined, hot blobs of putty was more than the sum of their individual masses.
We know that the masses of all the atoms in the blobs must be the same as they always were. The change is due to the change in `gamma` with heating, not to a change in mass. The heat energy, however, seems to be acting as if it was equivalent to some extra mass. If the quantity of heat is `E`, then it turns out that the extra mass `m` is such that `E=mc^2` (proof, p. 782).
But this whole argument was based on the fact that heat is a form of kinetic energy at the atomic level. Would `E=mc^2` apply to other forms of energy as well? Suppose a rocket ship contains some electrical energy stored in a battery. If we believed that `E=mc^2` applied to forms of kinetic energy but not to electrical energy, then we would have to believe that the pilot of the rocket could slow the ship down by using the battery to run a heater! This would not only be strange, but it would violate the principle of relativity, because the result of the experiment would be different depending on whether the ship was at rest or not. The only logical conclusion is that all forms of energy are equivalent to mass. Running the heater then has no effect on the motion of the ship, because the total energy in the ship was unchanged; one form of energy (electrical) was simply converted to another (heat).
The equation `E=mc^2` tells us how much energy is equivalent to how much mass: the conversion factor is the square of the speed of light, `c`. Since `c` a big number, you get a really really big number when you multiply it by itself to get `c^2`. This means that even a small amount of mass is equivalent to a very large amount of energy.
Example 8: Gravity bending light
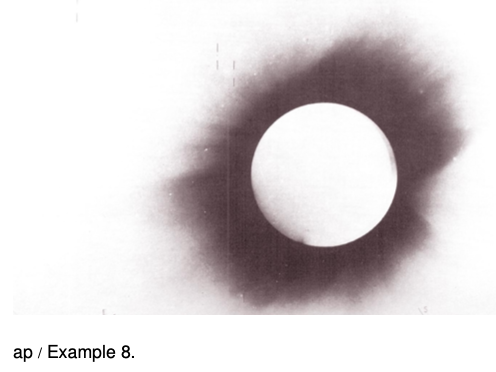
 Gravity is a universal attraction between things that have mass, and since the energy in a beam of light is equivalent to some very small amount of mass, we expect that light will be affected by gravity, although the effect should be very small. The first important experimental confirmation of relativity came in 1919 when stars next to the sun during a solar eclipse were observed to have shifted a little from their ordinary position. (If there was no eclipse, the glare of the sun would prevent the stars from being observed.) Starlight had been deflected by the sun's gravity. Figure ap is a photographic negative, so the circle that appears bright is actually the dark face of the moon, and the dark area is really the bright corona of the sun. The stars, marked by lines above and below them, appeared at positions slightly different than their normal ones.
Gravity is a universal attraction between things that have mass, and since the energy in a beam of light is equivalent to some very small amount of mass, we expect that light will be affected by gravity, although the effect should be very small. The first important experimental confirmation of relativity came in 1919 when stars next to the sun during a solar eclipse were observed to have shifted a little from their ordinary position. (If there was no eclipse, the glare of the sun would prevent the stars from being observed.) Starlight had been deflected by the sun's gravity. Figure ap is a photographic negative, so the circle that appears bright is actually the dark face of the moon, and the dark area is really the bright corona of the sun. The stars, marked by lines above and below them, appeared at positions slightly different than their normal ones.
Example 9: Black holes
A star with sufficiently strong gravity can prevent light from leaving. Quite a few black holes have been detected via their gravitational forces on neighboring stars or clouds of gas and dust.
You've learned about conservation of mass and conservation of energy, but now we see that they're not even separate conservation laws. As a consequence of the theory of relativity, mass and energy are equivalent, and are not separately conserved --- one can be converted into the other. Imagine that a magician waves his wand, and changes a bowl of dirt into a bowl of lettuce. You'd be impressed, because you were expecting that both dirt and lettuce would be conserved quantities. Neither one can be made to vanish, or to appear out of thin air. However, there are processes that can change one into the other. A farmer changes dirt into lettuce, and a compost heap changes lettuce into dirt. At the most fundamental level, lettuce and dirt aren't really different things at all; they're just collections of the same kinds of atoms --- carbon, hydrogen, and so on. Because mass and energy are like two different sides of the same coin, we may speak of mass-energy, a single conserved quantity, found by adding up all the mass and energy, with the appropriate conversion factor: `E=mc^2`.
Example 10: A rusting nail
`=>` An iron nail is left in a cup of water until it turns entirely to rust. The energy released is about 0.5 MJ. In theory, would a sufficiently precise scale register a change in mass? If so, how much?
`=>` The energy will appear as heat, which will be lost to the environment. The total mass-energy of the cup, water, and iron will indeed be lessened by 0.5 MJ. (If it had been perfectly insulated, there would have been no change, since the heat energy would have been trapped in the cup.) The speed of light is `c=3×10^8` meters per second, so converting to mass units, we have
`m=E/c^2`
`=(0.5×10^6 J)/((3×108 m"/"s)^2)`
`=6×10^(-12) "kilograms"`.
The change in mass is too small to measure with any practical technique. This is because the square of the speed of light is such a large number.
Example 11: Electron-positron annihilation
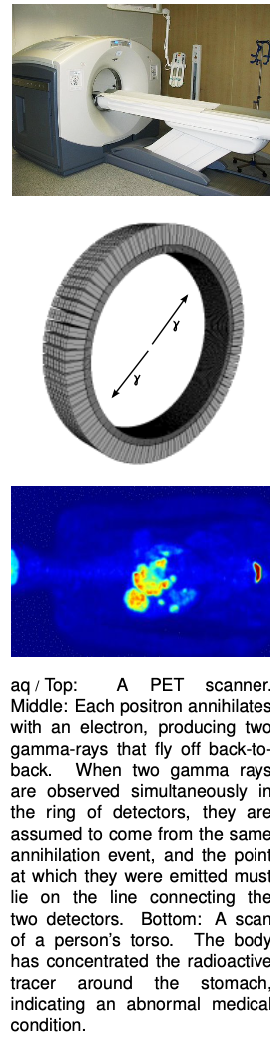 Natural radioactivity in the earth produces positrons, which are like electrons but have the opposite charge. A form of antimatter, positrons annihilate with electrons to produce gamma rays, a form of high-frequency light. Such a process would have been considered impossible before Einstein, because conservation of mass and energy were believed to be separate principles, and this process eliminates 100% of the original mass. The amount of energy produced by annihilating 1 kg of matter with 1 kg of antimatter is
Natural radioactivity in the earth produces positrons, which are like electrons but have the opposite charge. A form of antimatter, positrons annihilate with electrons to produce gamma rays, a form of high-frequency light. Such a process would have been considered impossible before Einstein, because conservation of mass and energy were believed to be separate principles, and this process eliminates 100% of the original mass. The amount of energy produced by annihilating 1 kg of matter with 1 kg of antimatter is
`E=mc^2`
`=(2 kg)(3.0×10^8 m"/"s)^2`
`=2×10^17 J`,
which is on the same order of magnitude as a day's energy consumption for the entire world's population!
Positron annihilation forms the basis for the medical imaging technique called a PET (positron emission tomography) scan, in which a positron-emitting chemical is injected into the patient and mapped by the emission of gamma rays from the parts of the body where it accumulates.
One commonly hears some misinterpretations of `mc^2`,
`mathcalE=mc^2` when `v=0`,
where the symbol `mathcalE` (cursive “E”) stands for mass-energy. The point of using the new symbol is simply to remind ourselves that we're talking about relativity, so an object at rest has `mathcalE=mc^2`, not `E=0` as we'd assume in classical physics.
Suppose we start accelerating the object with a constant force. A constant force means a constant rate of transfer of momentum, but `p=mgammav` approaches infinity as `v` approaches `c`, so the object will only get closer and closer to the speed of light, but never reach it. Now what about the work being done by the force? The force keeps doing work and doing work, which means that we keep on using up energy. Mass-energy is conserved, so the energy being expended must equal the increase in the object's mass-energy. We can continue this process for as long as we like, and the amount of mass-energy will increase without limit. We therefore conclude that an object's mass-energy approaches infinity as its speed approaches the speed of light,
`mathcalE->infty " when " v->c.`
Now that we have some idea what to expect, what is the actual equation for the mass-energy? As proved in my book Simple Nature, it is
`mathcalE=mgammac^2`.
self-check:
Verify that this equation has the two properties we wanted.
(answer in the back of the PDF version of the book)
Example 12: KE compared to `mc^2` at low speeds
`=>` An object is moving at ordinary nonrelativistic speeds. Compare its kinetic energy to the energy `mc^2` it has purely because of its mass.
`=>` The speed of light is a very big number, so `mc^2` is a huge number of joules. The object has a gigantic amount of energy because of its mass, and only a relatively small amount of additional kinetic energy because of its motion.
Another way of seeing this is that at low speeds, `gamma` is only a tiny bit greater than 1, so `mathcalE` is only a tiny bit greater than `mc^2`.
Example 13: The correspondence principle for mass-energy
`=>` Show that the equation `mathcalE=mgammac^2` obeys the correspondence principle.
`=>` As we accelerate an object from rest, its mass-energy becomes greater than its resting value. We interpret this excess mass-energy as the object's kinetic energy,
`KE=mathcalE(v)-mathcalE(v=0)`
`=mgammac^2-mc^2`
`=m(gamma-1)c^2`.
In example 2 on page 662, we found , so
which is the nonrelativistic expression. As demanded by the correspondence principle, relativity agrees with nonrelativistic physics at speeds that are small compared to the speed of light.
26.5 Relativistic mass and energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.