25.4 Decay by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
25.4 Decay
 Up until now I've soft-pedaled the fact that by changing the characteristics of an oscillator, it is possible to produce non-oscillatory behavior. For example, imagine taking the mass-on-a-spring system and making the spring weaker and weaker. In the limit of small `k`, it's as though there was no spring whatsoever, and the behavior of the system is that if you kick the mass, it simply starts slowing down.
Up until now I've soft-pedaled the fact that by changing the characteristics of an oscillator, it is possible to produce non-oscillatory behavior. For example, imagine taking the mass-on-a-spring system and making the spring weaker and weaker. In the limit of small `k`, it's as though there was no spring whatsoever, and the behavior of the system is that if you kick the mass, it simply starts slowing down.
For friction proportional to `v`, as we've been assuming, the result is that the velocity approaches zero, but never actually reaches zero. This is unrealistic for the mechanical oscillator, which will not have vanishing friction at low velocities, but it is quite realistic in the case of an electrical circuit, for which the voltage drop across the resistor really does approach zero as the current approaches zero.
Electrical circuits can exhibit all the same behavior. For simplicity we will analyze only the cases of LRC circuits with `L=0` or `C=0`.
The RC circuit
We first analyze the RC circuit, n. In reality one would have to “kick” the circuit, for example by briefly inserting a battery, in order to get any interesting behavior. We start with Ohm's law and the equation for the voltage across a capacitor:
`V_R=I_R`
The loop rule tells us
`V_R+V_C=0`,
and combining the three equations results in a relationship between `q` and `I`:
The negative sign tells us that the current tends to reduce the charge on the capacitor, i.e. to discharge it. It makes sense that the current is proportional to `q` : if `q` is large, then the attractive forces between the `+q` and `-q` charges on the plates of the capacitor are large, and charges will flow more quickly through the resistor in order to reunite. If there was zero charge on the capacitor plates, there would be no reason for current to flow. Since amperes, the unit of current, are the same as coulombs per second, it appears that the quantity `RC` must have units of seconds, and you can check for yourself that this is correct. `RC` is therefore referred to as the time constant of the circuit.
How exactly do `I` and `q` vary with time? Rewriting `I` as `Deltaq"/" Deltat`, we have
`(Deltaq)/(Deltat)=-1/(RC)q`.
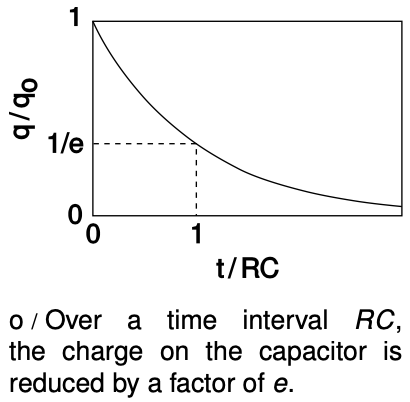 This equation describes a function `q(t)` that always gets smaller over time, and whose rate of decrease is big at first, when `q` is big, but gets smaller and smaller as `q` approaches zero. As an example of this type of mathematical behavior, we could imagine a man who has 1024 weeds in his backyard, and resolves to pull out half of them every day. On the first day, he pulls out half, and has 512 left. The next day, he pulls out half of the remaining ones, leaving 256. The sequence continues exponentially: 128, 64, 32, 16, 8, 4, 2, 1. Returning to our electrical example, the function `q(t)` apparently needs to be an exponential, which we can write in the form `ae^(bt)`, where `e=2.718...` is the base of natural logarithms. We could have written it with base 2, as in the story of the weeds, rather than base `e`, but the math later on turns out simpler if we use `e`. It doesn't make sense to plug a number that has units into a function like an exponential, so `bt` must be unitless, and `b` must therefore have units of inverse seconds. The number `b` quantifies how fast the exponential decay is. The only physical parameters of the circuit on which `b` could possibly depend are `R` and `C`, and the only way to put units of ohms and farads together to make units of inverse seconds is by computing `1"/"RC`. Well, actually we could use `7"/"RC` or `3pi"/"RC`, or any other unitless number divided by `RC`, but this is where the use of base `e` comes in handy: for base `e`, it turns out that the correct unitless constant is 1. Thus our solution is
This equation describes a function `q(t)` that always gets smaller over time, and whose rate of decrease is big at first, when `q` is big, but gets smaller and smaller as `q` approaches zero. As an example of this type of mathematical behavior, we could imagine a man who has 1024 weeds in his backyard, and resolves to pull out half of them every day. On the first day, he pulls out half, and has 512 left. The next day, he pulls out half of the remaining ones, leaving 256. The sequence continues exponentially: 128, 64, 32, 16, 8, 4, 2, 1. Returning to our electrical example, the function `q(t)` apparently needs to be an exponential, which we can write in the form `ae^(bt)`, where `e=2.718...` is the base of natural logarithms. We could have written it with base 2, as in the story of the weeds, rather than base `e`, but the math later on turns out simpler if we use `e`. It doesn't make sense to plug a number that has units into a function like an exponential, so `bt` must be unitless, and `b` must therefore have units of inverse seconds. The number `b` quantifies how fast the exponential decay is. The only physical parameters of the circuit on which `b` could possibly depend are `R` and `C`, and the only way to put units of ohms and farads together to make units of inverse seconds is by computing `1"/"RC`. Well, actually we could use `7"/"RC` or `3pi"/"RC`, or any other unitless number divided by `RC`, but this is where the use of base `e` comes in handy: for base `e`, it turns out that the correct unitless constant is 1. Thus our solution is
`q=q_oexp*(-t/(RC))`.
The number `RC`, with units of seconds, is called the RC time constant of the circuit, and it tells us how long we have to wait if we want the charge to fall off by a factor of `1"/"e`.
The RL circuit
 The RL circuit, p, can be attacked by similar methods, and it can easily be shown that it gives
The RL circuit, p, can be attacked by similar methods, and it can easily be shown that it gives
`I=I_oexp*(-R/Lt).`
The `RL` time constant equals `L"/"R`.
Example 6: Death by solenoid; spark plugs
When we suddenly break an RL circuit, what will happen? It might seem that we're faced with a paradox, since we only have two forms of energy, magnetic energy and heat, and if the current stops suddenly, the magnetic field must collapse suddenly. But where does the lost magnetic energy go? It can't go into resistive heating of the resistor, because the circuit has now been broken, and current can't flow!
The way out of this conundrum is to recognize that the open gap in the circuit has a resistance which is large, but not infinite. This large resistance causes the RL time constant `L"/"R` to be very small. The current thus continues to flow for a very brief time, and flows straight across the air gap where the circuit has been opened. In other words, there is a spark!
We can determine based on several different lines of reasoning that the voltage drop from one end of the spark to the other must be very large. First, the air's resistance is large, so [Private Equation] requires a large voltage. We can also reason that all the energy in the magnetic field is being dissipated in a short time, so the power dissipated in the spark, , is large, and this requires a large value of `V`. (`I` isn't large --- it is decreasing from its initial value.) Yet a third way to reach the same result is to consider the equation `V_L=(DeltaI)/(Deltat)`: since the time constant is short, the time derivative `DeltaI"/"Deltat` is large.
This is exactly how a car's spark plugs work. Another application is to electrical safety: it can be dangerous to break an inductive circuit suddenly, because so much energy is released in a short time. There is also no guarantee that the spark will discharge across the air gap; it might go through your body instead, since your body might have a lower resistance.
Discussion Question
A A gopher gnaws through one of the wires in the DC lighting system in your front yard, and the lights turn off. At the instant when the circuit becomes open, we can consider the bare ends of the wire to be like the plates of a capacitor, with an air gap (or gopher gap) between them. What kind of capacitance value are we talking about here? What would this tell you about the `RC` time constant?
25.4 Decay by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.