24.3 The universal speed `c` by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
24.3 The universal speed `c`
 Let's think a little more about the role of the `45`-degree diagonal in the Lorentz transformation. Slopes on these graphs are interpreted as velocities. This line has a slope of `1` in relativistic units, but that slope corresponds to `c` in ordinary metric units. We already know that the relativistic distance unit must be extremely large compared to the relativistic time unit, so `c` must be extremely large. Now note what happens when we perform a Lorentz transformation: this particular line gets stretched, but the new version of the line lies right on top of the old one, and its slope stays the same. In other words, if one observer says that something has a velocity equal to `c`, every other observer will agree on that velocity as well. (The same thing happens with `-c`.)
Let's think a little more about the role of the `45`-degree diagonal in the Lorentz transformation. Slopes on these graphs are interpreted as velocities. This line has a slope of `1` in relativistic units, but that slope corresponds to `c` in ordinary metric units. We already know that the relativistic distance unit must be extremely large compared to the relativistic time unit, so `c` must be extremely large. Now note what happens when we perform a Lorentz transformation: this particular line gets stretched, but the new version of the line lies right on top of the old one, and its slope stays the same. In other words, if one observer says that something has a velocity equal to `c`, every other observer will agree on that velocity as well. (The same thing happens with `-c`.)
Velocities don't simply add and subtract.
This is counterintuitive, since we expect velocities to add and subtract in relative motion. If a dog is running away from me at `5` m/s relative to the sidewalk, and I run after it at `3` m/s, the dog's velocity in my frame of reference is `2` m/s. According to everything we have learned about motion (p. 82), the dog must have different speeds in the two frames: `5` m/s in the sidewalk's frame and `2` m/s in mine. But velocities are measured by dividing a distance by a time, and both distance and time are distorted by relativistic effects, so we actually shouldn't expect the ordinary arithmetic addition of velocities to hold in relativity; it's an approximation that's valid at velocities that are small compared to `c`.
A universal speed limit
 For example, suppose Janet takes a trip in a spaceship, and accelerates until she is moving at `0.6c` relative to the earth. She then launches a space probe in the forward direction at a speed relative to her ship of `0.6c`. We might think that the probe was then moving at a velocity of `1.2c`, but in fact the answer is still less than `c` (problem 1, page 700). This is an example of a more general fact about relativity, which is that `c` represents a universal speed limit. This is required by causality, as shown in figure h.
For example, suppose Janet takes a trip in a spaceship, and accelerates until she is moving at `0.6c` relative to the earth. She then launches a space probe in the forward direction at a speed relative to her ship of `0.6c`. We might think that the probe was then moving at a velocity of `1.2c`, but in fact the answer is still less than `c` (problem 1, page 700). This is an example of a more general fact about relativity, which is that `c` represents a universal speed limit. This is required by causality, as shown in figure h.
Light travels at `c`.
Now consider a beam of light. We're used to talking casually about the “speed of light,” but what does that really mean? Motion is relative, so normally if we want to talk about a velocity, we have to specify what it's measured relative to. A sound wave has a certain speed relative to the air, and a water wave has its own speed relative to the water. If we want to measure the speed of an ocean wave, for example, we should make sure to measure it in a frame of reference at rest relative to the water. But light isn't a vibration of a physical medium; it can propagate through the near-perfect vacuum of outer space, as when rays of sunlight travel to earth. This seems like a paradox: light is supposed to have a specific speed, but there is no way to decide what frame of reference to measure it in. The way out of the paradox is that light must travel at a velocity equal to `c`. Since all observers agree on a velocity of `c`, regardless of their frame of reference, everything is consistent.
The Michelson-Morley experiment
The constancy of the speed of light had in fact already been observed when Einstein was an 8-year-old boy, but because nobody could figure out how to interpret it, the result was largely ignored. In 1887 Michelson and Morley set up a clever apparatus to measure any difference in the speed of light beams traveling east-west and north-south. The motion of the earth around the sun at `110,000` km/hour (about `0.01%` of the speed of light) is to our west during the day. Michelson and Morley believed that light was a vibration of a mysterious medium called the ether, so they expected that the speed of light would be a fixed value relative to the ether. As the earth moved through the ether, they thought they would observe an effect on the velocity of light along an east-west line. For instance, if they released a beam of light in a westward direction during the day, they expected that it would move away from them at less than the normal speed because the earth was chasing it through the ether. They were surprised when they found that the expected `0.01%` change in the speed of light did not occur.

Discussion Questions
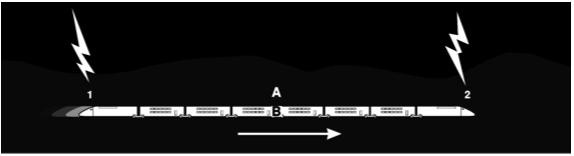
A The figure shows a famous thought experiment devised by Einstein. A train is moving at constant velocity to the right when bolts of lightning strike the ground near its front and back. Alice, standing on the dirt at the midpoint of the flashes, observes that the light from the two flashes arrives simultaneously, so she says the two strikes must have occurred simultaneously. Bob, meanwhile, is sitting aboard the train, at its middle. He passes by Alice at the moment when Alice later figures out that the flashes happened. Later, he receives flash `2`, and then flash `1`. He infers that since both flashes traveled half the length of the train, flash `2` must have occurred first. How can this be reconciled with Alice's belief that the flashes were simultaneous? Explain using a graph.
B Use a graph to resolve the following relativity paradox. Relativity says that in one frame of reference, event A could happen before event B, but in someone else's frame B would come before A. How can this be? Obviously the two people could meet up at A and talk as they cruised past each other. Wouldn't they have to agree on whether B had already happened?
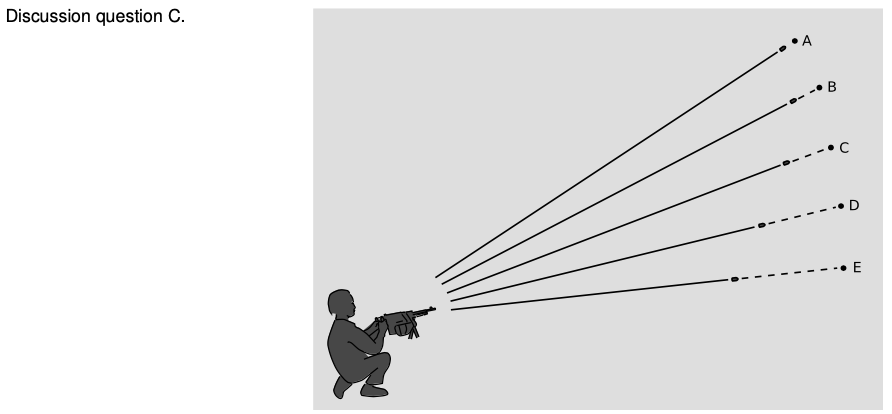
C The machine-gunner in the figure sends out a spray of bullets. Suppose that the bullets are being shot into outer space, and that the distances traveled are trillions of miles (so that the human figure in the diagram is not to scale). After a long time, the bullets reach the points shown with dots which are all equally far from the gun. Their arrivals at those points are events `A` through `E`, which happen at different times. The chain of impacts extends across space at a speed greater than `c`. Does this violate special relativity?
24.3 The universal speed `c` by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.