23.3 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Notation
`gamma`....................an abbreviation for `1/sqrt(1-v^2/c^2)` (Lorentz Factor)
Summary
Experiments show that space and time do not have the properties claimed by Galileo and Newton. Time and space as seen by one observer are distorted compared to another observer's perceptions if they are moving relative to each other. This distortion is quantified by the factor
`gamma=1/sqrt(1-v^2/c^2)` (Lorentz Factor),
where `v` is the relative velocity of the two observers, and `c` is a universal velocity that is the same in all frames of reference. Light travels at c. A clock appears to run fastest to an observer who is not in motion relative to it, and appears to run too slowly by a factor of `gamma` to an observer who has a velocity `v` relative to the clock. Similarly, a meter-stick appears longest to an observer who sees it at rest, and appears shorter to other observers. Time and space are relative, not absolute.
As a consequence of relativity, we must have not just electrical interactions of charges with charges, but also an additional magnetic interaction of moving charges with other moving charges.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem
1. What happens in the equation for `gamma` when you put in a negative number for `v`? Explain what this means physically, and why it makes sense.
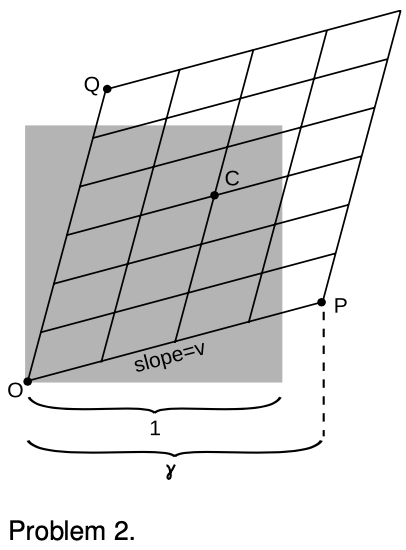2. In this homework problem, you'll fill in the steps of the algebra required in order to find the equation for `gamma` on page 659. To keep the algebra simple, let the time `t` in figure n equal 1, as suggested in the figure accompanying this homework problem. The original square then has an area of 1, and the transformed parallelogram must also have an area of 1. (a) Prove that point P is at `x=vgamma`, so that its `(t,x)` coordinates are `(gamma,vgamma)`. (b) Find the `(t,x)` coordinates of point Q. (c) Find the length of the short diagonal connecting P and Q. (d) Average the coordinates of P and Q to find the coordinates of the midpoint C of the parallelogram, and then find distance OC. (e) Find the area of the parallelogram by computing twice the area of triangle PQO. [Hint: You can take PQ to be the base of the triangle.] (f) Set this area equal to 1 and solve for `gamma` to prove `gamma=1/sqrt(1-v^2)`. `sqrt`
3. Astronauts in three different spaceships are communicating with each other. Those aboard ships A and B agree on the rate at which time is passing, but they disagree with the ones on ship C.
(a) Alice is aboard ship A. How does she describe the motion of her own ship, in its frame of reference?
(b) Describe the motion of the other two ships according to Alice.
(c) Give the description according to Betty, whose frame of reference is ship B.
(d) Do the same for Cathy, aboard ship C.
4. The Voyager 1 space probe, launched in 1977, is moving faster relative to the earth than any other human-made object, at 17,000 meters per second.
(a) Calculate the probe's `gamma`.
(b) Over the course of one year on earth, slightly less than one year passes on the probe. How much less? (There are 31 million seconds in a year.) `sqrt`
5. The earth is orbiting the sun, and therefore is contracted relativistically in the direction of its motion. Compute the amount by which its diameter shrinks in this direction. `sqrt`
6. Page 654 lists five observed properties of space and time that sufficed to derive relativity. There are other sets of postulates that could also have been used, and in fact this was not the set that was first used by Einstein. Suppose that our first inkling that spacetime isn't Galilean consists of an experiment like the one in figure aa on p. 668, and that we interpret it, correctly, as being evidence of a relativistic length contraction as in figure ac on p. 669. Besides this fact, what else is needed in order to get the full structure of relativity?
23.3 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.