23.1 Relativistic distortion of space and time by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
23.1 Relativistic distortion of space and time
Time distortion arising from motion and gravity
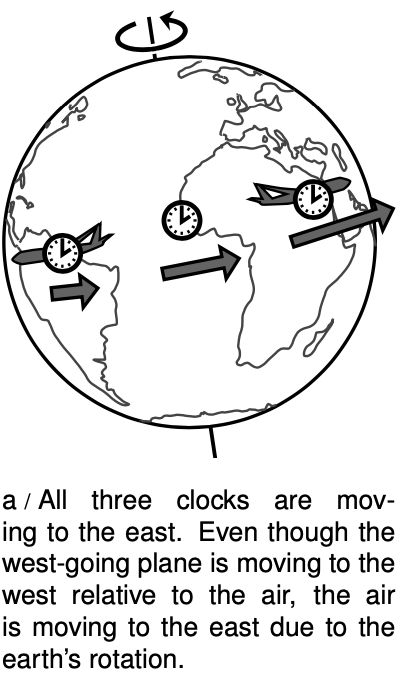 Let's refer back to the results of the Hafele-Keating experiment described on p. 618. Hafele and Keating were testing specific quantitative predictions of relativity, and they verified them to within their experiment's error bars. Let's work backward instead, and inspect the empirical results for clues as to how time works.
Let's refer back to the results of the Hafele-Keating experiment described on p. 618. Hafele and Keating were testing specific quantitative predictions of relativity, and they verified them to within their experiment's error bars. Let's work backward instead, and inspect the empirical results for clues as to how time works.
The east-going clock lost time, ending up off by -59±10 nanoseconds, while the west-going one gained 273±7 ns. Since two traveling clocks experienced effects in opposite directions, we can tell that the rate at which time flows depends on the motion of the observer. The east-going clock was moving in the same direction as the earth's rotation, so its velocity relative to the earth's center was greater than that of the clock that remained in Washington, while the west-going clock's velocity was correspondingly reduced. The fact that the east-going clock fell behind, and the west-going one got ahead, shows that the effect of motion is to make time go more slowly. This effect of motion on time was predicted by Einstein in his original 1905 paper on relativity, written when he was 26.
If this had been the only effect in the Hafele-Keating experiment, then we would have expected to see effects on the two flying clocks that were equal in size. Making up some simple numbers to keep the arithmetic transparent, suppose that the earth rotates from west to east at `1000` km/hr, and that the planes fly at `300` km/hr. Then the speed of the clock on the ground is `1000` km/hr, the speed of the clock on the east-going plane is `1300` km/hr, and that of the west-going clock `700` km/hr. Since the speeds of `700`, `1000`, and `1300` km/hr have equal spacing on either side of `1000`, we would expect the discrepancies of the moving clocks relative to the one in the lab to be equal in size but opposite in sign.
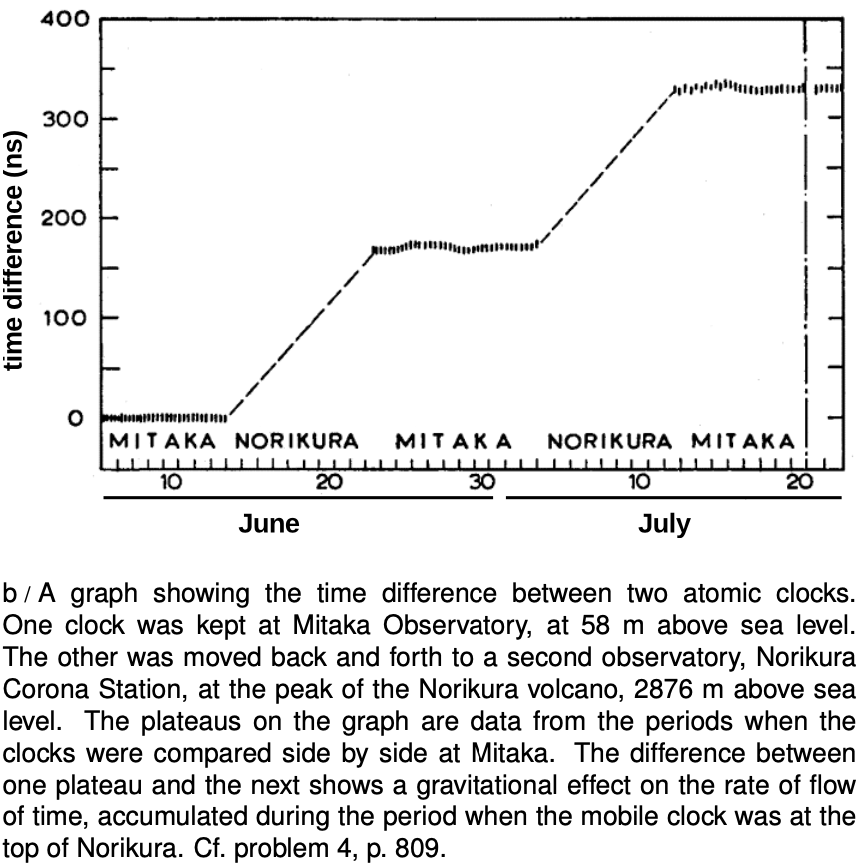
In fact, the two effects are unequal in size: -59 ns and 273 ns. This implies that there is a second effect involved, a speeding up of time simply due to the planes' being up in the air. This was verified more directly in a 1978 experiment by Iijima and Fujiwara, figure b, in which identical atomic clocks were kept at rest at the top and bottom of a mountain near Tokyo. This experiment, unlike the Hafele-Keating one, isolates one effect on time, the gravitational one: time's rate of flow increases with height in a gravitational field. Einstein didn't figure out how to incorporate gravity into relativity until 1915, after much frustration and many false starts. The simpler version of the theory without gravity is known as special relativity, the full version as general relativity. We'll restrict ourselves to special relativity until chapter 27, and that means that what we want to focus on right now is the distortion of time due to motion, not gravity.
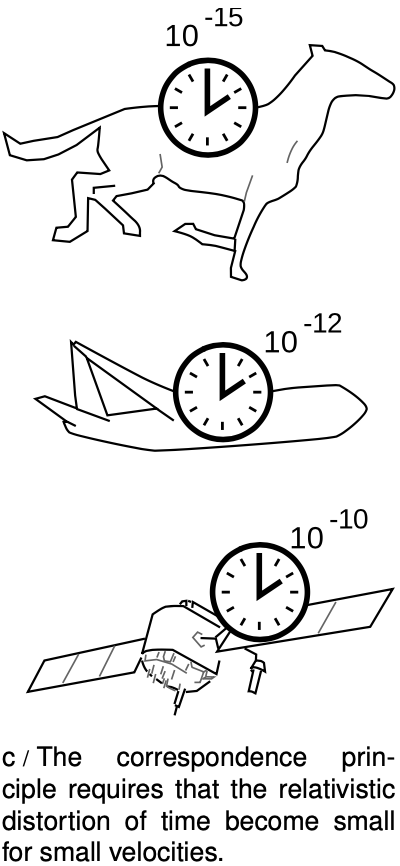 We can now see in more detail how to apply the correspondence principle. The behavior of the three clocks in the Hafele-Keating experiment shows that the amount of time distortion increases as the speed of the clock's motion increases. Newton lived in an era when the fastest mode of transportation was a galloping horse, and the best pendulum clocks would accumulate errors of perhaps a minute over the course of several days. A horse is much slower than a jet plane, so the distortion of time would have had a relative size of only ~ 10-15 --- much smaller than the clocks were capable of detecting. At the speed of a passenger jet, the effect is about 10-12, and state-of-the-art atomic clocks in 1971 were capable of measuring that. A GPS satellite travels much faster than a jet airplane, and the effect on the satellite turns out to be ~ 10-10. The general idea here is that all physical laws are approximations, and approximations aren't simply right or wrong in different situations. Approximations are better or worse in different situations, and the question is whether a particular approximation is good enough in a given situation to serve a particular purpose. The faster the motion, the worse the Newtonian approximation of absolute time. Whether the approximation is good enough depends on what you're trying to accomplish. The correspondence principle says that the approximation must have been good enough to explain all the experiments done in the centuries before Einstein came up with relativity.
We can now see in more detail how to apply the correspondence principle. The behavior of the three clocks in the Hafele-Keating experiment shows that the amount of time distortion increases as the speed of the clock's motion increases. Newton lived in an era when the fastest mode of transportation was a galloping horse, and the best pendulum clocks would accumulate errors of perhaps a minute over the course of several days. A horse is much slower than a jet plane, so the distortion of time would have had a relative size of only ~ 10-15 --- much smaller than the clocks were capable of detecting. At the speed of a passenger jet, the effect is about 10-12, and state-of-the-art atomic clocks in 1971 were capable of measuring that. A GPS satellite travels much faster than a jet airplane, and the effect on the satellite turns out to be ~ 10-10. The general idea here is that all physical laws are approximations, and approximations aren't simply right or wrong in different situations. Approximations are better or worse in different situations, and the question is whether a particular approximation is good enough in a given situation to serve a particular purpose. The faster the motion, the worse the Newtonian approximation of absolute time. Whether the approximation is good enough depends on what you're trying to accomplish. The correspondence principle says that the approximation must have been good enough to explain all the experiments done in the centuries before Einstein came up with relativity.
By the way, don't get an inflated idea of the importance of these atomic clock experiments. Special relativity had already been confirmed by a vast and varied body of experiments decades before the 1970's. The only reason I'm giving such a prominent role to these experiments, which were actually more important as tests of general relativity, is that they were conceptually very direct. It would be nice to have an equally simple and transparent atomic clock experiment in which only the effect of motion was singled out, with no gravitational effect. Example 3 on page 662 describes how something along these lines was eventually carried out, forty years after the Hafele-Keating experiment.
The Lorentz transformation
Relativity says that when two observers are in different frames of reference, each observer considers the other one's perception of time to be distorted. We'll also see that something similar happens to their observations of distances, so both space and time are distorted. What exactly is this distortion? How do we even conceptualize it?
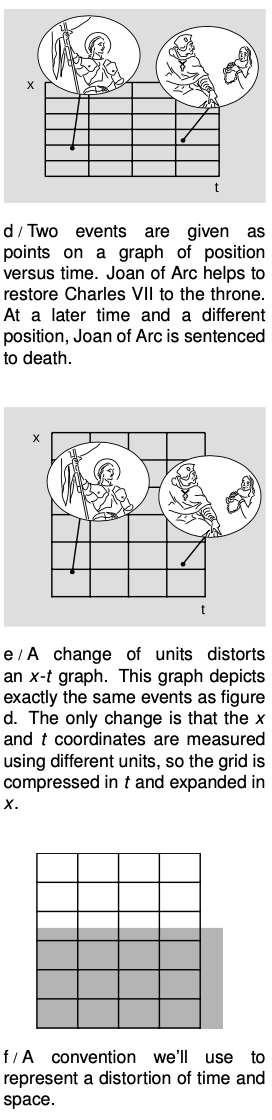 The idea isn't really as radical as it might seem at first. We can visualize the structure of space and time using a graph with position and time on its axes. These graphs are familiar by now, but we're going to look at them in a slightly different way. Before, we used them to describe the motion of objects. The grid underlying the graph was merely the stage on which the actors played their parts. Now the background comes to the foreground: it's time and space themselves that we're studying. We don't necessarily need to have a line or a curve drawn on top of the grid to represent a particular object. We may, for example, just want to talk about events, depicted as points on the graph as in figure d. A distortion of the Cartesian grid underlying the graph can arise for perfectly ordinary reasons that Newton would have readily accepted. For example, we can simply change the units used to measure time and position, as in figure e.
The idea isn't really as radical as it might seem at first. We can visualize the structure of space and time using a graph with position and time on its axes. These graphs are familiar by now, but we're going to look at them in a slightly different way. Before, we used them to describe the motion of objects. The grid underlying the graph was merely the stage on which the actors played their parts. Now the background comes to the foreground: it's time and space themselves that we're studying. We don't necessarily need to have a line or a curve drawn on top of the grid to represent a particular object. We may, for example, just want to talk about events, depicted as points on the graph as in figure d. A distortion of the Cartesian grid underlying the graph can arise for perfectly ordinary reasons that Newton would have readily accepted. For example, we can simply change the units used to measure time and position, as in figure e.
We're going to have quite a few examples of this type, so I'll adopt the convention shown in figure f for depicting them. Figure f summarizes the relationship between figures d and e in a more compact form. The gray rectangle represents the original coordinate grid of figure d, while the grid of black lines represents the new version from figure e. Omitting the grid from the gray rectangle makes the diagram easier to decode visually.
Our goal of unraveling the mysteries of special relativity amounts to nothing more than finding out how to draw a diagram like f in the case where the two different sets of coordinates represent measurements of time and space made by two different observers, each in motion relative to the other. Galileo and Newton thought they knew the answer to this question, but their answer turned out to be only approximately right. To avoid repeating the same mistakes, we need to clearly spell out what we think are the basic properties of time and space that will be a reliable foundation for our reasoning. I want to emphasize that there is no purely logical way of deciding on this list of properties. The ones I'll list are simply a summary of the patterns observed in the results from a large body of experiments. Furthermore, some of them are only approximate. For example, property 1 below is only a good approximation when the gravitational field is weak, so it is a property that applies to special relativity, not to general relativity.
Experiments show that:
- No point in time or space has properties that make it different from any other point.
- Likewise, all directions in space have the same properties.
- Motion is relative, i.e., all inertial frames of reference are equally valid.
- Causality holds, in the sense described on page 619.
- Time depends on the state of motion of the observer.
Most of these are not very subversive. Properties 1 and 2 date back to the time when Galileo and Newton started applying the same universal laws of motion to the solar system and to the earth; this contradicted Aristotle, who believed that, for example, a rock would naturally want to move in a certain special direction (down) in order to reach a certain special location (the earth's surface). Property 3 is the reason that Einstein called his theory “relativity,” but Galileo and Newton believed exactly the same thing to be true, as dramatized by Galileo's run-in with the Church over the question of whether the earth could really be in motion around the sun. Example 3 on p. 243 describes a modern, high-precision experiment that can be interpreted as a test of this principle. Property 4 would probably surprise most people only because it asserts in such a weak and specialized way something that they feel deeply must be true. The only really strange item on the list is 5, but the Hafele-Keating experiment forces it upon us.
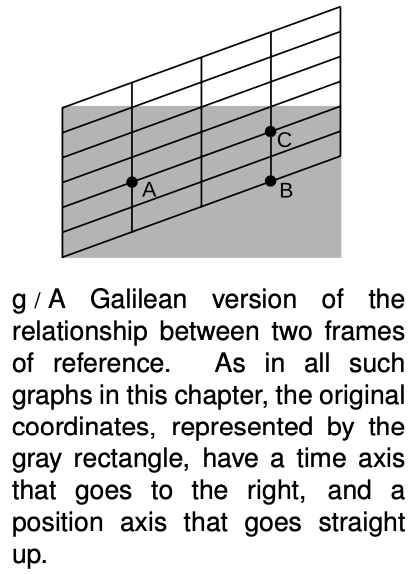 If it were not for property 5, we could imagine that figure g would give the correct transformation between frames of reference in motion relative to one another. Let's say that observer 1, whose grid coincides with the gray rectangle, is a hitch-hiker standing by the side of a road. Event A is a raindrop hitting his head, and event B is another raindrop hitting his head. He says that A and B occur at the same location in space. Observer 2 is a motorist who drives by without stopping; to him, the passenger compartment of his car is at rest, while the asphalt slides by underneath. He says that A and B occur at different points in space, because during the time between the first raindrop and the second, the hitch-hiker has moved backward. On the other hand, observer 2 says that events A and C occur in the same place, while the hitch-hiker disagrees. The slope of the grid-lines is simply the velocity of the relative motion of each observer relative to the other.
If it were not for property 5, we could imagine that figure g would give the correct transformation between frames of reference in motion relative to one another. Let's say that observer 1, whose grid coincides with the gray rectangle, is a hitch-hiker standing by the side of a road. Event A is a raindrop hitting his head, and event B is another raindrop hitting his head. He says that A and B occur at the same location in space. Observer 2 is a motorist who drives by without stopping; to him, the passenger compartment of his car is at rest, while the asphalt slides by underneath. He says that A and B occur at different points in space, because during the time between the first raindrop and the second, the hitch-hiker has moved backward. On the other hand, observer 2 says that events A and C occur in the same place, while the hitch-hiker disagrees. The slope of the grid-lines is simply the velocity of the relative motion of each observer relative to the other.
Figure g has familiar, comforting, and eminently sensible behavior, but it also happens to be wrong, because it violates property 5. The distortion of the coordinate grid has only moved the vertical lines up and down, so both observers agree that events like B and C are simultaneous. If this was really the way things worked, then all observers could synchronize all their clocks with one another for once and for all, and the clocks would never get out of sync. This contradicts the results of the Hafele-Keating experiment, in which all three clocks were initially synchronized in Washington, but later went out of sync because of their different states of motion.
It might seem as though we still had a huge amount of wiggle room available for the correct form of the distortion. It turns out, however, that properties 1-5 are sufficient to prove that there is only one answer, which is the one found by Einstein in 1905. To see why this is, let's work by a process of elimination.
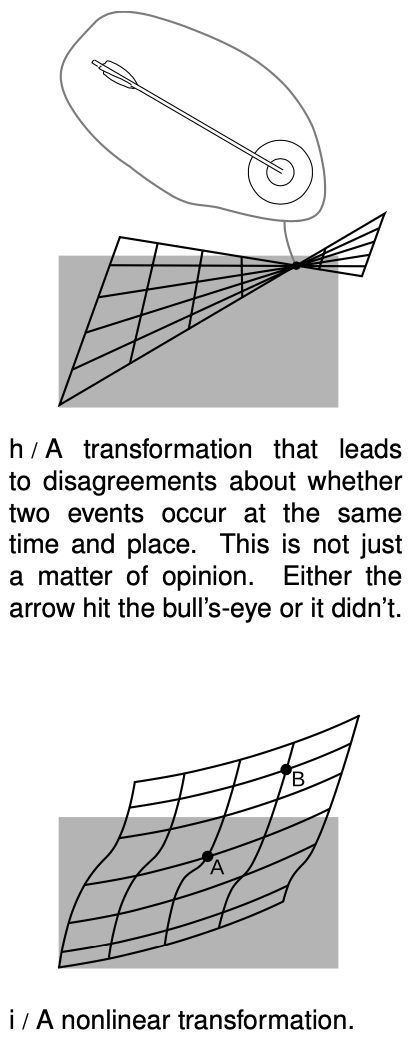 Figure h shows a transformation that might seem at first glance to be as good a candidate as any other, but it violates property 3, that motion is relative, for the following reason. In observer 2's frame of reference, some of the grid lines cross one another. This means that observers 1 and 2 disagree on whether or not certain events are the same. For instance, suppose that event A marks the arrival of an arrow at the bull's-eye of a target, and event B is the location and time when the bull's-eye is punctured. Events A and B occur at the same location and at the same time. If one observer says that A and B coincide, but another says that they don't, we have a direct contradiction. Since the two frames of reference in figure h give contradictory results, one of them is right and one is wrong. This violates property 3, because all inertial frames of reference are supposed to be equally valid. To avoid problems like this, we clearly need to make sure that none of the grid lines ever cross one another.
Figure h shows a transformation that might seem at first glance to be as good a candidate as any other, but it violates property 3, that motion is relative, for the following reason. In observer 2's frame of reference, some of the grid lines cross one another. This means that observers 1 and 2 disagree on whether or not certain events are the same. For instance, suppose that event A marks the arrival of an arrow at the bull's-eye of a target, and event B is the location and time when the bull's-eye is punctured. Events A and B occur at the same location and at the same time. If one observer says that A and B coincide, but another says that they don't, we have a direct contradiction. Since the two frames of reference in figure h give contradictory results, one of them is right and one is wrong. This violates property 3, because all inertial frames of reference are supposed to be equally valid. To avoid problems like this, we clearly need to make sure that none of the grid lines ever cross one another.
The next type of transformation we want to kill off is shown in figure i, in which the grid lines curve, but never cross one another. The trouble with this one is that it violates property 1, the uniformity of time and space. The transformation is unusually “twisty” at A, whereas at B it's much more smooth. This can't be correct, because the transformation is only supposed to depend on the relative state of motion of the two frames of reference, and that given information doesn't single out a special role for any particular point in spacetime. If, for example, we had one frame of reference rotating relative to the other, then there would be something special about the axis of rotation. But we're only talking about inertial frames of reference here, as specified in property 3, so we can't have rotation; each frame of reference has to be moving in a straight line at constant speed. For frames related in this way, there is nothing that could single out an event like A for special treatment compared to B, so transformation i violates property 1.
The examples in figures h and i show that the transformation we're looking for must be linear, meaning that it must transform lines into lines, and furthermore that it has to take parallel lines to parallel lines. Einstein wrote in his 1905 paper that “... on account of the property of homogeneity [property 1] which we ascribe to time and space, the [transformation] must be linear.”Applying this to our diagrams, the original gray rectangle, which is a special type of parallelogram containing right angles, must be transformed into another parallelogram. There are three types of transformations, figure j, that have this property. Case I is the Galilean transformation of figure g on page 655, which we've already ruled out.
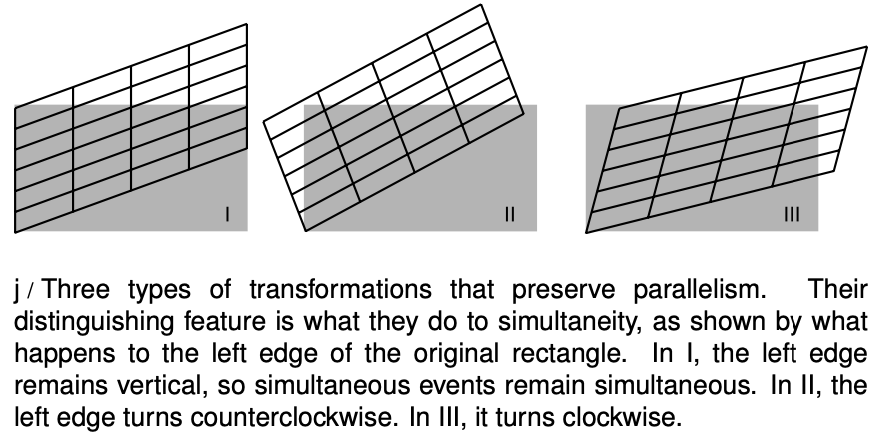
Case II can also be discarded. Here every point on the grid rotates counterclockwise. What physical parameter would determine the amount of rotation? The only thing that could be relevant would be `v`, the relative velocity of the motion of the two frames of reference with respect to one another. But if the angle of rotation was proportional to `v`, then for large enough velocities the grid would have left and right reversed, and this would violate property 4, causality: one observer would say that event A caused a later event B, but another observer would say that B came first and caused A.
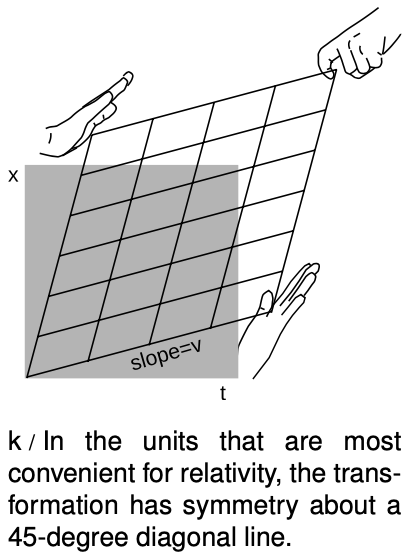 The only remaining possibility is case III, which I've redrawn in figure k with a couple of changes. This is the one that Einstein predicted in 1905. The transformation is known as the Lorentz transformation, after Hendrik Lorentz (1853-1928), who partially anticipated Einstein's work, without arriving at the correct interpretation. The distortion is a kind of smooshing and stretching, as suggested by the hands. Also, we've already seen in figures d-f on page 654 that we're free to stretch or compress everything as much as we like in the horizontal and vertical directions, because this simply corresponds to changing the units of measurement for time and distance. In figure k I've chosen units that give the whole drawing a convenient symmetry about a 45-degree diagonal line. Ordinarily it wouldn't make sense to talk about a 45-degree angle on a graph whose axes had different units. But in relativity, the symmetric appearance of the transformation tells us that space and time ought to be treated on the same footing, and measured in the same units.
The only remaining possibility is case III, which I've redrawn in figure k with a couple of changes. This is the one that Einstein predicted in 1905. The transformation is known as the Lorentz transformation, after Hendrik Lorentz (1853-1928), who partially anticipated Einstein's work, without arriving at the correct interpretation. The distortion is a kind of smooshing and stretching, as suggested by the hands. Also, we've already seen in figures d-f on page 654 that we're free to stretch or compress everything as much as we like in the horizontal and vertical directions, because this simply corresponds to changing the units of measurement for time and distance. In figure k I've chosen units that give the whole drawing a convenient symmetry about a 45-degree diagonal line. Ordinarily it wouldn't make sense to talk about a 45-degree angle on a graph whose axes had different units. But in relativity, the symmetric appearance of the transformation tells us that space and time ought to be treated on the same footing, and measured in the same units.
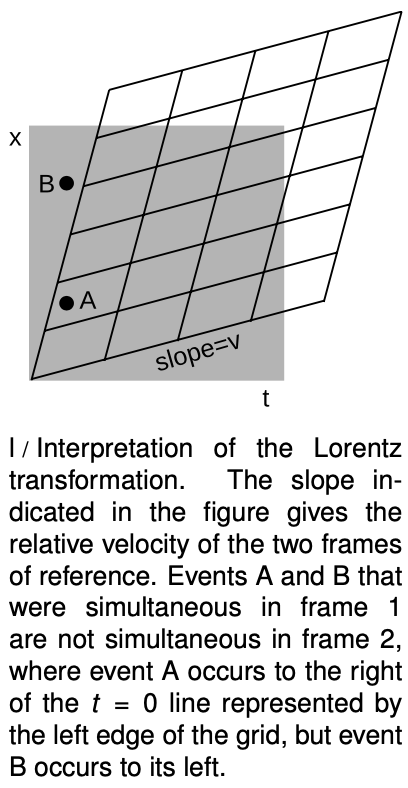 As in our discussion of the Galilean transformation, slopes are interpreted as velocities, and the slope of the near-horizontal lines in figure l is interpreted as the relative velocity of the two observers. The difference between the Galilean version and the relativistic one is that now there is smooshing happening from the other side as well. Lines that were vertical in the original grid, representing simultaneous events, now slant over to the right. This tells us that, as required by property 5, different observers do not agree on whether events that occur in different places are simultaneous. The Hafele-Keating experiment tells us that this non-simultaneity effect is fairly small, even when the velocity is as big as that of a passenger jet, and this is what we would have anticipated by the correspondence principle. The way that this is expressed in the graph is that if we pick the time unit to be the second, then the distance unit turns out to be hundreds of thousands of miles. In these units, the velocity of a passenger jet is an extremely small number, so the slope `v` in a figure like l is extremely small, and the amount of distortion is tiny --- it would be much too small to see on this scale.
As in our discussion of the Galilean transformation, slopes are interpreted as velocities, and the slope of the near-horizontal lines in figure l is interpreted as the relative velocity of the two observers. The difference between the Galilean version and the relativistic one is that now there is smooshing happening from the other side as well. Lines that were vertical in the original grid, representing simultaneous events, now slant over to the right. This tells us that, as required by property 5, different observers do not agree on whether events that occur in different places are simultaneous. The Hafele-Keating experiment tells us that this non-simultaneity effect is fairly small, even when the velocity is as big as that of a passenger jet, and this is what we would have anticipated by the correspondence principle. The way that this is expressed in the graph is that if we pick the time unit to be the second, then the distance unit turns out to be hundreds of thousands of miles. In these units, the velocity of a passenger jet is an extremely small number, so the slope `v` in a figure like l is extremely small, and the amount of distortion is tiny --- it would be much too small to see on this scale.
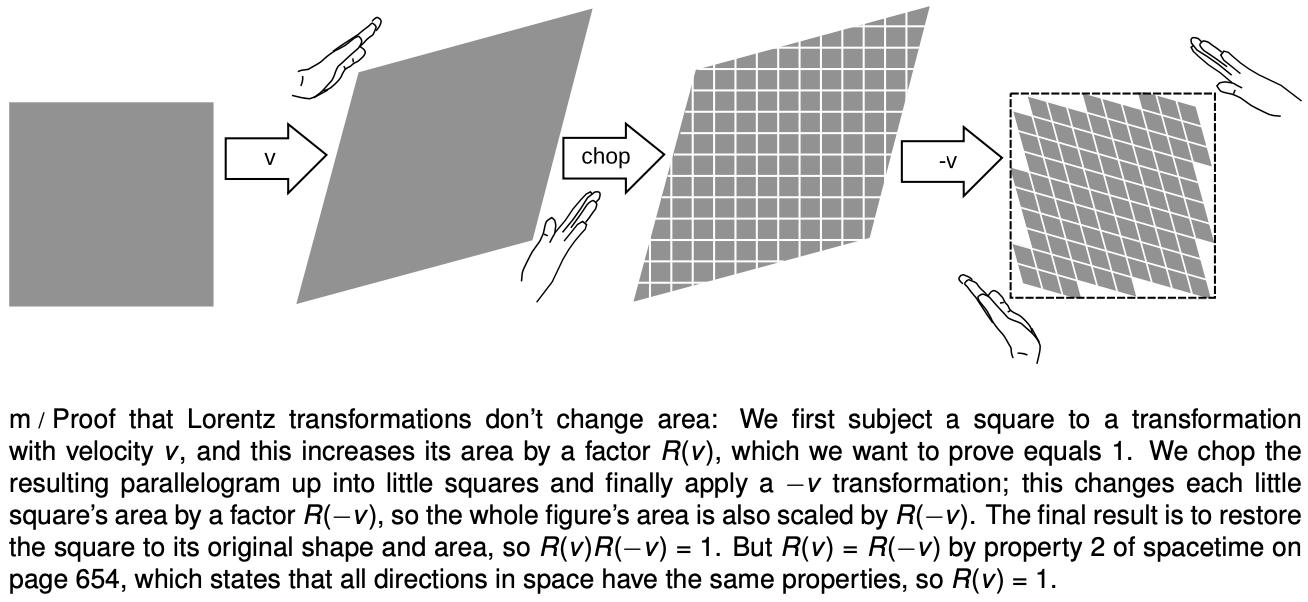
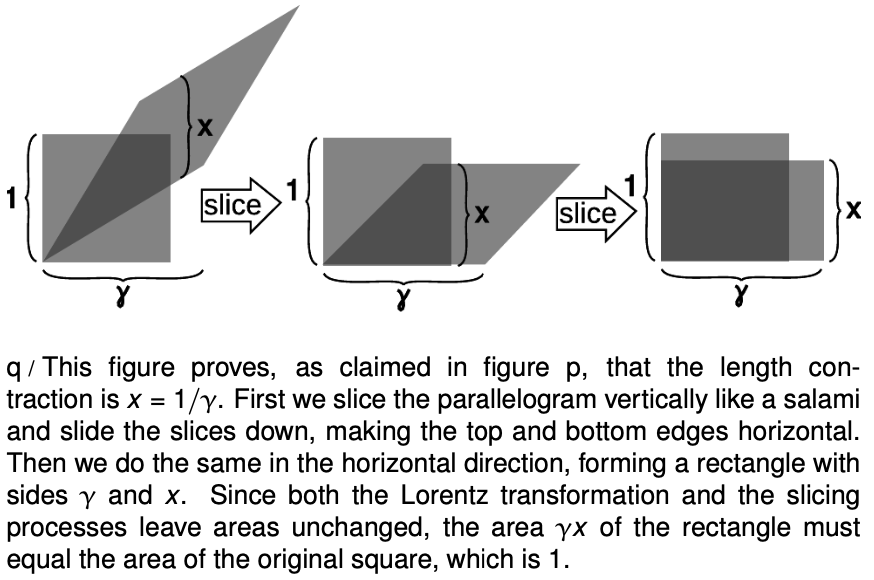
The only thing left to determine about the Lorentz transformation is the size of the transformed parallelogram relative to the size of the original one. Although the drawing of the hands in figure k may suggest that the grid deforms like a framework made of rigid coat-hanger wire, that is not the case. If you look carefully at the figure, you'll see that the edges of the smooshed parallelogram are actually a little longer than the edges of the original rectangle. In fact what stays the same is not lengths but areas, as proved in the caption to figure m.
The γ factor
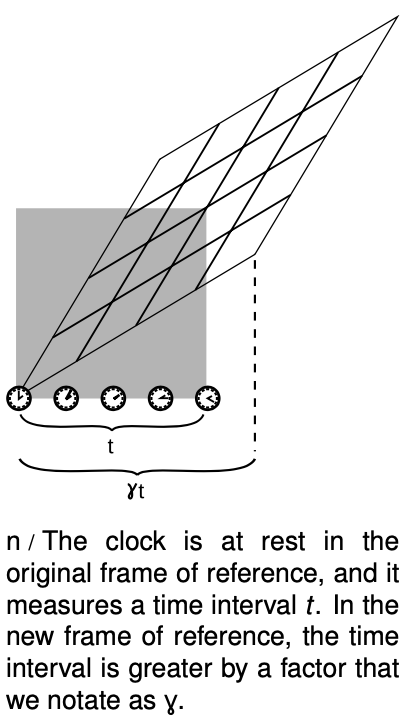 Figure l showed us that observers in different frames disagree on whether different events are simultaneous. This is an indication that time is not absolute, so we shouldn't be surprised that time's rate of flow is also different for different observers. We use the symbol `gamma` (Greek letter gamma) defined in the figure n to measure this unequal rate of flow. With a little algebra and geometry (homework problem 2, page 673), one can use the equal-area property to show that this ratio is given by
Figure l showed us that observers in different frames disagree on whether different events are simultaneous. This is an indication that time is not absolute, so we shouldn't be surprised that time's rate of flow is also different for different observers. We use the symbol `gamma` (Greek letter gamma) defined in the figure n to measure this unequal rate of flow. With a little algebra and geometry (homework problem 2, page 673), one can use the equal-area property to show that this ratio is given by
`gamma=1/sqrt(1-v^2`
 When we say, “It's five hours from LA to Vegas,” we're using a unit of time as a unit of distance. This works because there is a standard speed implied: the speed of a car on the freeway. Similarly, the conversion factor c can be interpreted as a speed, so that v/c is the unitless ratio of two speeds. As argued on p. 619, cause and effect can never be propagated instantaneously; c turns out to be the specific numerical speed limit on cause and effect. In particular, we'll see in section 24.3 that light travels at c, which has a numerical value of 3.0×108 m/s.
When we say, “It's five hours from LA to Vegas,” we're using a unit of time as a unit of distance. This works because there is a standard speed implied: the speed of a car on the freeway. Similarly, the conversion factor c can be interpreted as a speed, so that v/c is the unitless ratio of two speeds. As argued on p. 619, cause and effect can never be propagated instantaneously; c turns out to be the specific numerical speed limit on cause and effect. In particular, we'll see in section 24.3 that light travels at c, which has a numerical value of 3.0×108 m/s.
Because γ is always greater than 1, we have the following interpretation:
Time dilation
 A clock runs fastest in the frame of reference of an observer who is at rest relative to the clock. An observer in motion relative to the clock at speed `v` perceives the clock as running more slowly by a factor of `gamma`.
A clock runs fastest in the frame of reference of an observer who is at rest relative to the clock. An observer in motion relative to the clock at speed `v` perceives the clock as running more slowly by a factor of `gamma`.
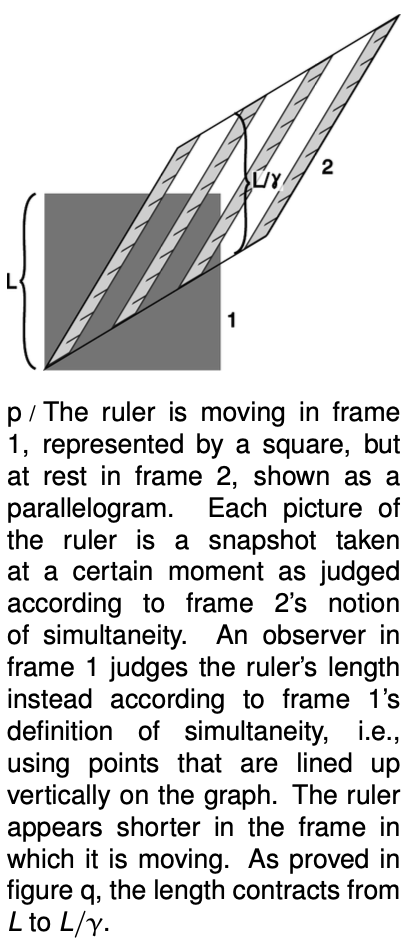
As proved in figures p and q, lengths are also distorted:
Length contraction
A meter-stick appears longest to an observer who is at rest relative to it. An observer moving relative to the meter-stick at `v` observes the stick to be shortened by a factor of `gamma`.
self-check:
What is γ when v=0? What does this mean?
(answer in the back of the PDF version of the book)
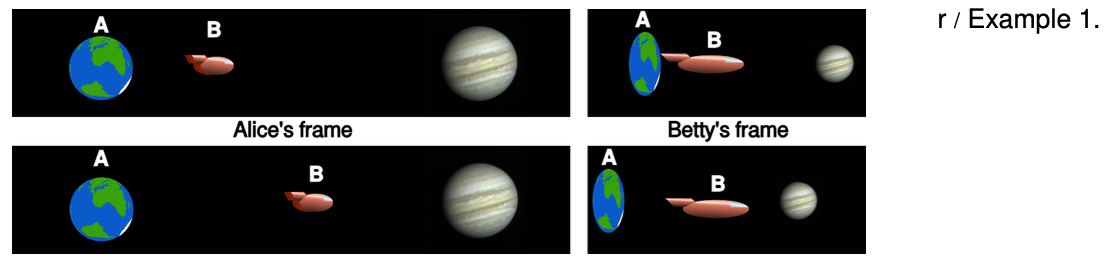
Example 1: An interstellar road trip
Alice stays on earth while her twin Betty heads off in a spaceship for Tau Ceti, a nearby star. Tau Ceti is 12 light-years away, so even though Betty travels at 87% of the speed of light, it will take her a long time to get there: 14 years, according to Alice.
Betty experiences time dilation. At this speed, her `gamma` is 2.0, so that the voyage will only seem to her to last 7 years. But there is perfect symmetry between Alice's and Betty's frames of reference, so Betty agrees with Alice on their relative speed; Betty sees herself as being at rest, while the sun and Tau Ceti both move backward at 87% of the speed of light. How, then, can she observe Tau Ceti to get to her in only 7 years, when it should take 14 years to travel 12 light-years at this speed?
We need to take into account length contraction. Betty sees the distance between the sun and Tau Ceti to be shrunk by a factor of 2. The same thing occurs for Alice, who observes Betty and her spaceship to be foreshortened.
Example 2: The correspondence principle
 The correspondence principle requires that `gamma` be close to 1 for the velocities much less than `c` encountered in everyday life. Let's explicitly find the amount `epsilon` by which `gamma` differs from 1, when `v` is small. Let `gamma=1+epsilon`. The definition of `gamma` gives `1=gamma^2(1-v^2"/"c^2)`, so `1=(1+2epsilon+epsilon^2)(1-v^2"/"c^2)approx1+2epsilon-v^2"/"c^2`, where the approximation comes from discarding very small terms such as `epsilon^2` and `epsilonv^2"/"c^2`. We find `epsilon=v^2/(2c^2)`. As expected, this will be small when `v` is small compared to `c`.
The correspondence principle requires that `gamma` be close to 1 for the velocities much less than `c` encountered in everyday life. Let's explicitly find the amount `epsilon` by which `gamma` differs from 1, when `v` is small. Let `gamma=1+epsilon`. The definition of `gamma` gives `1=gamma^2(1-v^2"/"c^2)`, so `1=(1+2epsilon+epsilon^2)(1-v^2"/"c^2)approx1+2epsilon-v^2"/"c^2`, where the approximation comes from discarding very small terms such as `epsilon^2` and `epsilonv^2"/"c^2`. We find `epsilon=v^2/(2c^2)`. As expected, this will be small when `v` is small compared to `c`.
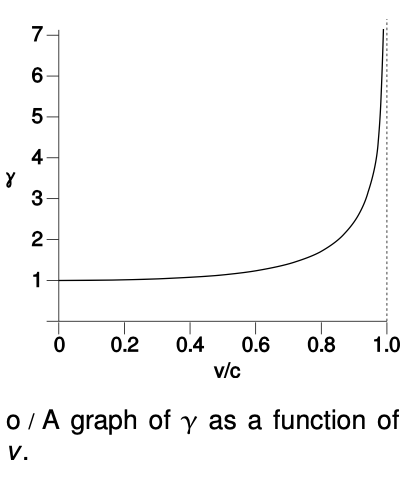
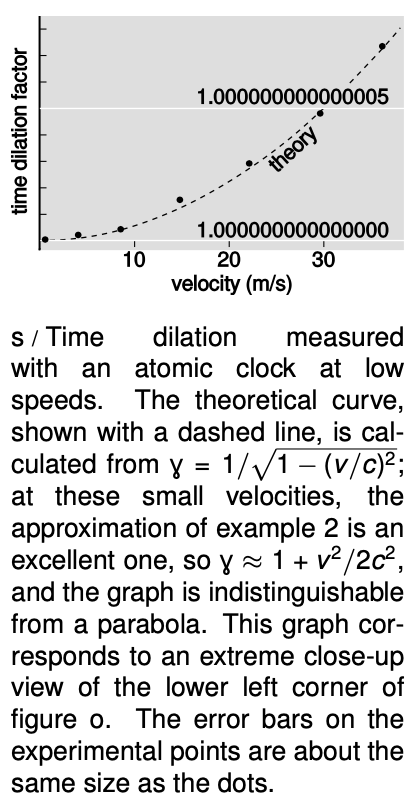
Figure o shows that the approximation found in example 2 is not valid for large values of `v"/"c`. In fact, `gamma` blows up to infinity as `v` gets closer and closer to `c`.
Example 3: A moving atomic clock
Example 2 shows that when `v` is small, relativistic effects are approximately proportional to `v^2`, so it is very difficult to observe them at low speeds. For example, a car on the freeway travels at about 1/10 the speed of a passenger jet, so the resulting time dilation is only 1/100 as much. For this reason, it was not until four decades after Hafele and Keating that anyone did a conceptually simple atomic clock experiment in which the only effect was motion, not gravity; it is difficult to move a clock at a high enough velocity without putting it in some kind of aircraft, which then has to fly at some altitude. In 2010, however, Chou et al. succeeded in building an atomic clock accurate enough to detect time dilation at speeds as low as 10 m/s. Figure s shows their results. Since it was not practical to move the entire clock, the experimenters only moved the aluminum atoms inside the clock that actually made it “tick.”

Example 4: Large time dilation
The time dilation effect in the Hafele-Keating experiment was very small. If we want to see a large time dilation effect, we can't do it with something the size of the atomic clocks they used; the kinetic energy would be greater than the total megatonnage of all the world's nuclear arsenals. We can, however, accelerate subatomic particles to speeds at which `gamma` is large. For experimental particle physicists, relativity is something you do all day before heading home and stopping off at the store for milk. An early, low-precision experiment of this kind was performed by Rossi and Hall in 1941, using naturally occurring cosmic rays. Figure t shows a 1974 experiment of a similar type which verified the time dilation predicted by relativity to a precision of about one part per thousand.
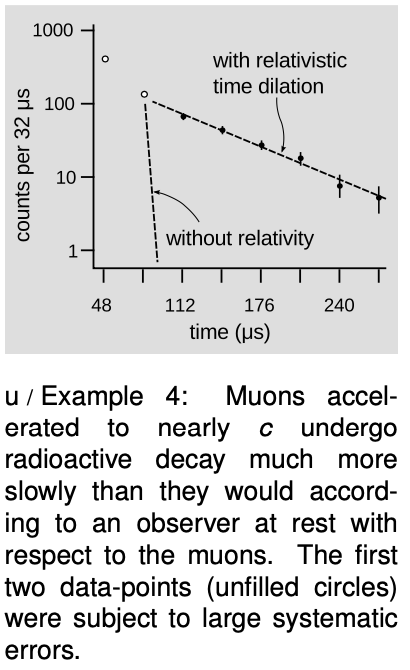 Particles called muons (named after the Greek letter `mu`, “myoo”) were produced by an accelerator at CERN, near Geneva. A muon is essentially a heavier version of the electron. Muons undergo radioactive decay, lasting an average of only 2.197 `mu`s before they evaporate into an electron and two neutrinos. The 1974 experiment was actually built in order to measure the magnetic properties of muons, but it produced a high-precision test of time dilation as a byproduct. Because muons have the same electric charge as electrons, they can be trapped using magnetic fields. Muons were injected into the ring shown in figure t, circling around it until they underwent radioactive decay. At the speed at which these muons were traveling, they had `gamma=29.33`, so on the average they lasted 29.33 times longer than the normal lifetime. In other words, they were like tiny alarm clocks that self-destructed at a randomly selected time. Figure u shows the number of radioactive decays counted, as a function of the time elapsed after a given stream of muons was injected into the storage ring. The two dashed lines show the rates of decay predicted with and without relativity. The relativistic line is the one that agrees with experiment.
Particles called muons (named after the Greek letter `mu`, “myoo”) were produced by an accelerator at CERN, near Geneva. A muon is essentially a heavier version of the electron. Muons undergo radioactive decay, lasting an average of only 2.197 `mu`s before they evaporate into an electron and two neutrinos. The 1974 experiment was actually built in order to measure the magnetic properties of muons, but it produced a high-precision test of time dilation as a byproduct. Because muons have the same electric charge as electrons, they can be trapped using magnetic fields. Muons were injected into the ring shown in figure t, circling around it until they underwent radioactive decay. At the speed at which these muons were traveling, they had `gamma=29.33`, so on the average they lasted 29.33 times longer than the normal lifetime. In other words, they were like tiny alarm clocks that self-destructed at a randomly selected time. Figure u shows the number of radioactive decays counted, as a function of the time elapsed after a given stream of muons was injected into the storage ring. The two dashed lines show the rates of decay predicted with and without relativity. The relativistic line is the one that agrees with experiment.
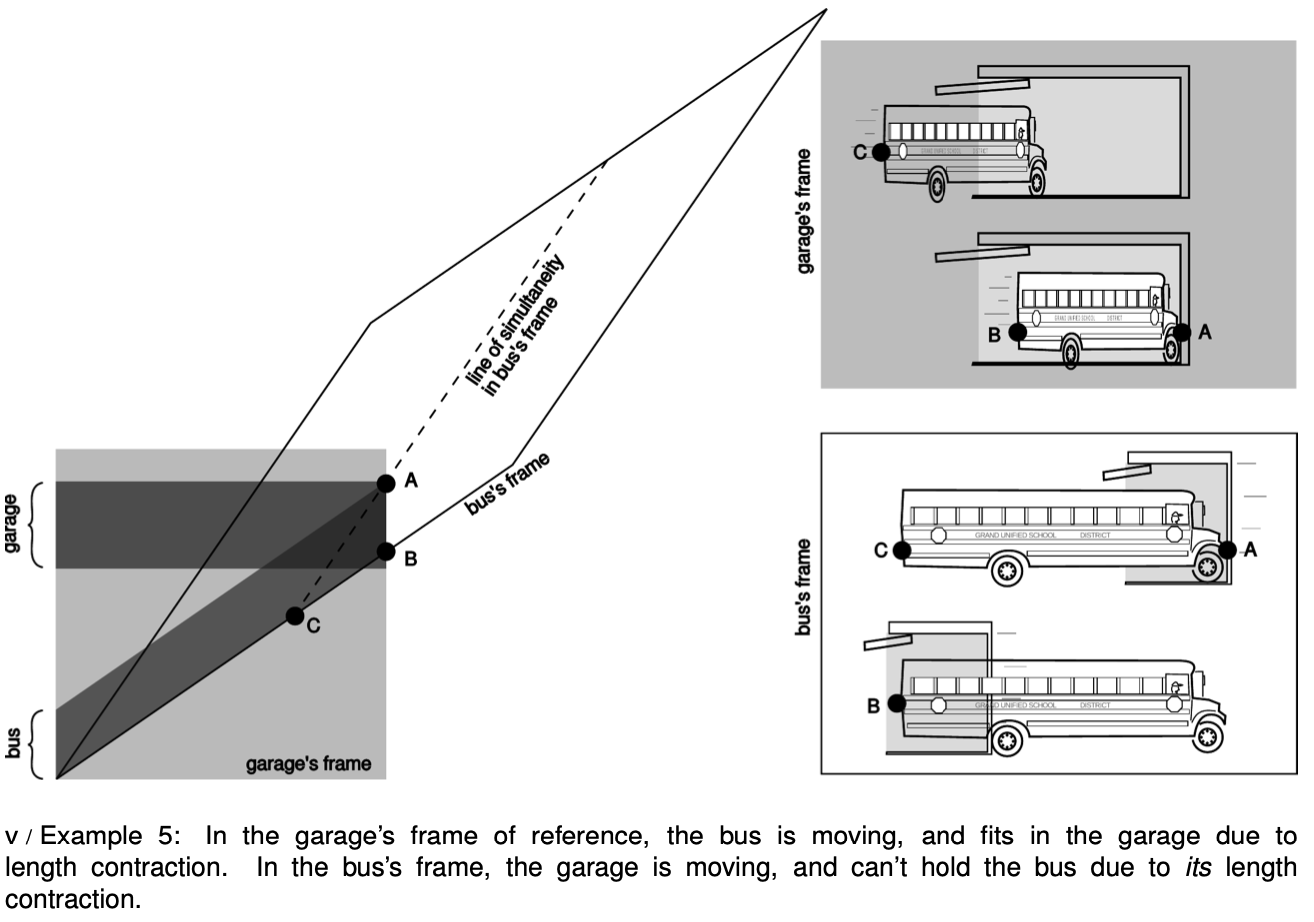
Example 5: The garage paradox
Suppose we take a schoolbus and drive it at relativistic speeds into a garage of ordinary size, in which it normally would not fit. Because of the length contraction, it fits. But the driver will perceive thegarage as being contracted and thus even less able to contain the bus.
The paradox is resolved when we recognize that the concept of fitting the bus in the garage “all at once” contains a hidden assumption, the assumption that it makes sense to ask whether the front and back of the bus can simultaneously be in the garage. Observers in different frames of reference moving at high relative speeds do not necessarily agree on whether things happen simultaneously. As shown in figure v, the person in the garage's frame can shut the door at an instant B he perceives to be simultaneous with the front bumper's arrival A at the back wall of the garage, but the driver would not agree about the simultaneity of these two events, and would perceive the door as having shut long after she plowed through the back wall.
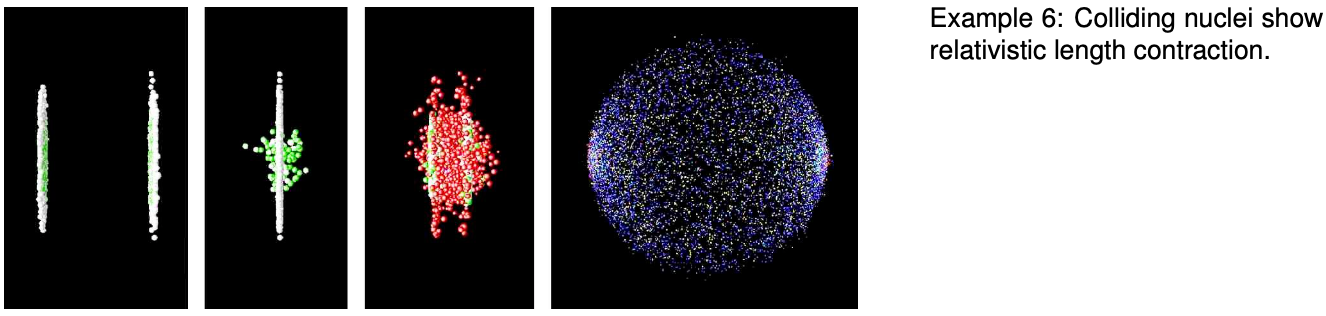
Example 6: An example of length contraction
Figure w shows an artist's rendering of the length contraction for the collision of two gold nuclei at relativistic speeds in the RHIC accelerator in Long Island, New York, which went on line in 2000. The gold nuclei would appear nearly spherical (or just slightly lengthened like an American football) in frames moving along with them, but in the laboratory's frame, they both appear drastically foreshortened as they approach the point of collision. The later pictures show the nuclei merging to form a hot soup, in which experimenters hope to observe a new form of matter.
Discussion Questions
A: A person in a spaceship moving at 99.99999999% of the speed of light relative to Earth shines a flashlight forward through dusty air, so the beam is visible. What does she see? What would it look like to an observer on Earth?
 B: A question that students often struggle with is whether time and space can really be distorted, or whether it just seems that way. Compare with optical illusions or magic tricks. How could you verify, for instance, that the lines in the figure are actually parallel? Are relativistic effects the same, or not?
B: A question that students often struggle with is whether time and space can really be distorted, or whether it just seems that way. Compare with optical illusions or magic tricks. How could you verify, for instance, that the lines in the figure are actually parallel? Are relativistic effects the same, or not?
C: On a spaceship moving at relativistic speeds, would a lecture seem even longer and more boring than normal?
D: Mechanical clocks can be affected by motion. For example, it was a significant technological achievement to build a clock that could sail aboard a ship and still keep accurate time, allowing longitude to be determined. How is this similar to or different from relativistic time dilation?
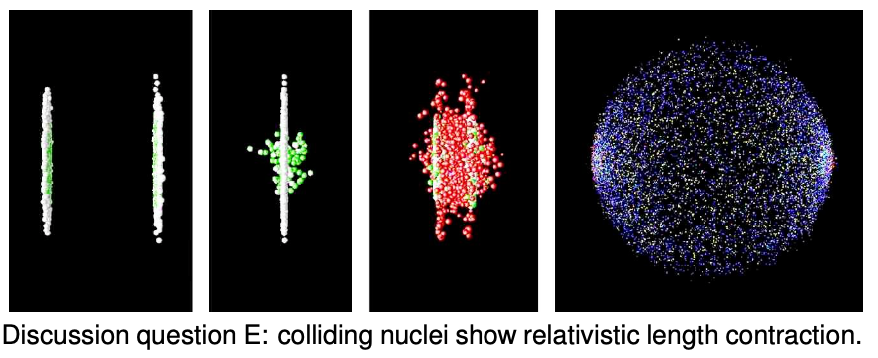
E: Figure w from page 665, depicting the collision of two nuclei at the RHIC accelerator, is reproduced below. What would the shapes of the two nuclei look like to a microscopic observer riding on the left-hand nucleus? To an observer riding on the right-hand one? Can they agree on what is happening? If not, why not --- after all, shouldn't they see the same thing if they both compare the two nuclei side-by-side at the same instant in time?
 F: If you stick a piece of foam rubber out the window of your car while driving down the freeway, the wind may compress it a little. Does it make sense to interpret the relativistic length contraction as a type of strain that pushes an object's atoms together like this? How does this relate to discussion question ?
F: If you stick a piece of foam rubber out the window of your car while driving down the freeway, the wind may compress it a little. Does it make sense to interpret the relativistic length contraction as a type of strain that pushes an object's atoms together like this? How does this relate to discussion question ?
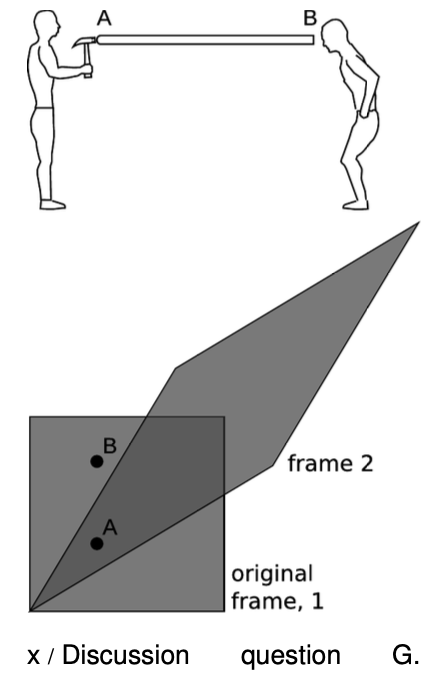
G: The rod in the figure is perfectly rigid. At event A, the hammer strikes one end of the rod. At event B, the other end moves. Since the rod is perfectly rigid, it can't compress, so A and B are simultaneous. In frame 2, B happens before A. Did the motion at the right end cause the person on the left to decide to pick up the hammer and use it?
23.1 Relativistic distortion of space and time by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.