22.4 Calculating energy in fields by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
22.4 Calculating energy in fields
We found on p. 620 that fields have energy, and we now know as well that fields act like vectors. Presumably there is a relationship between the strength of a field and its energy density. Flipping the direction of the field can't change the density of energy, which is a scalar and therefore has no direction in space. We therefore expect that the energy density to be proportional to the square of the field, so that changing E to -E has no effect on the result. This is exactly what we've already learned to expect for waves: the energy depends on the square of the amplitude. The relevant equations for the gravitational and electric fields are as follows:
(energy stored in the gravitational field per m3)`=-1/(8piG)|g|^2`
(energy stored in the electric field per m3)`=1/(8pik)|E|^2`
A similar expression is given on p. 681 for the magnetic field.
Although funny factors of `8pi` and the plus and minus signs may have initially caught your eye, they are not the main point. The important idea is that the energy density is proportional to the square of the field strength in all cases. We first give a simple numerical example and work a little on the concepts, and then turn our attention to the factors out in front.
In chapter 22 when we discussed the original reason for introducing the concept of a field of force, a prime motivation was that otherwise there was no way to account for the energy transfers involved when forces were delayed by an intervening distance. We used to think of the universe's energy as consisting of
kinetic energy
+gravitational potential energy based on the distances between objects that interact gravitationally
+electric potential energy based on the distances between objects that interact electrically
+magnetic potential energy based on the distances between objects that interact magnetically,
but in none static situations we must use a different method:
kinetic energy
+gravitational potential energy stored in gravitational fields
+electric potential energy stored in electric fields
+magnetic potential stored in magnetic fields
Surprisingly, the new method still gives the same answers for the static cases.
Example 9: Energy stored in a capacitor
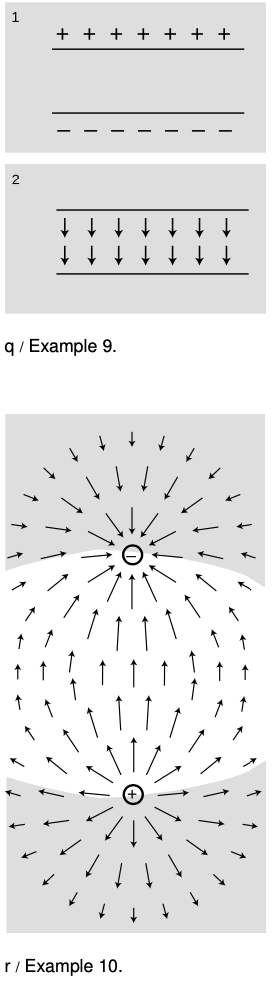 A pair of parallel metal plates, seen from the side in figure q, can be used to store electrical energy by putting positive charge on one side and negative charge on the other. Such a device is called a capacitor. (We have encountered such an arrangement previously, but there its purpose was to deflect a beam of electrons, not to store energy.)
A pair of parallel metal plates, seen from the side in figure q, can be used to store electrical energy by putting positive charge on one side and negative charge on the other. Such a device is called a capacitor. (We have encountered such an arrangement previously, but there its purpose was to deflect a beam of electrons, not to store energy.)
In the old method of describing potential energy, 1, we think in terms of the mechanical work that had to be done to separate the positive and negative charges onto the two plates, working against their electrical attraction. The new description, 2, attributes the storage of energy to the newly created electric field occupying the volume between the plates. Since this is a static case, both methods give the same, correct answer.
Example 10: Potential energy of a pair of opposite charges
Imagine taking two opposite charges, r, that were initially far apart and allowing them to come together under the influence of their electrical attraction.
According to the old method, potential energy is lost because the electric force did positive work as it brought the charges together. (This makes sense because as they come together and accelerate it is their potential energy that is being lost and converted to kinetic energy.)
By the new method, we must ask how the energy stored in the electric field has changed. In the region indicated approximately by the shading in the figure, the superposing fields of the two charges undergo partial cancellation because they are in opposing directions. The energy in the shaded region is reduced by this effect. In the unshaded region, the fields reinforce, and the energy is increased.
It would be quite a project to do an actual numerical calculation of the energy gained and lost in the two regions (this is a case where the old method of finding energy gives greater ease of computation), but it is fairly easy to convince oneself that the energy is less when the charges are closer. This is because bringing the charges together shrinks the high-energy unshaded region and enlarges the low-energy shaded region.
Example 11: Energy transmitted by ripples in the electric and magnetic fields
We'll see in chapter 24 that phenomena like light, radio waves, and x-rays are all ripples in the electric and magnetic fields. The old method would give zero energy for a region of space containing a light wave but no charges. That would be wrong! We can only use the old method in static cases.
Now let's give at least some justification for the other features of the expressions for energy density, `-1/(8piG)|g|^2` and `1/(8pik)|E|^2`, besides the proportionality to the square of the field strength.
First, why the different plus and minus signs? The basic idea is that the signs have to be opposite in the gravitational and electric cases because there is an attraction between two positive masses (which are the only kind that exist), but two positive charges would repel. Since we've already seen examples where the positive sign in the electric energy makes sense, the gravitational energy equation must be the one with the minus sign.
It may also seem strange that the constants `G` and `k` are in the denominator. They tell us how strong the three different forces are, so shouldn't they be on top? No. Consider, for instance, an alternative universe in which gravity is twice as strong as in ours. The numerical value of `G` is doubled. Because `G` is doubled, all the gravitational field strengths are doubled as well, which quadruples the quantity `|g|^2`. In the expression `-1/(8piG)|g|^2`, we have quadrupled something on top and doubled something on the bottom, which makes the energy twice as big. That makes perfect sense.
Discussion Questions
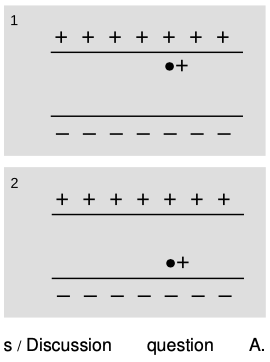 A The figure shows a positive charge in the gap between two capacitor plates. First make a large drawing of the field pattern that would be formed by the capacitor itself, without the extra charge in the middle. Next, show how the field pattern changes when you add the particle at these two positions. Compare the energy of the electric fields in the two cases. Does this agree with what you would have expected based on your knowledge of electrical forces?
A The figure shows a positive charge in the gap between two capacitor plates. First make a large drawing of the field pattern that would be formed by the capacitor itself, without the extra charge in the middle. Next, show how the field pattern changes when you add the particle at these two positions. Compare the energy of the electric fields in the two cases. Does this agree with what you would have expected based on your knowledge of electrical forces?
B Criticize the following statement: “A solenoid makes a charge in the space surrounding it, which dissipates when you release the energy.”
C In example 10, I argued that the fields surrounding a positive and negative charge contain less energy when the charges are closer together. Perhaps a simpler approach is to consider the two extreme possibilities: the case where the charges are infinitely far apart, and the one in which they are at zero distance from each other, i.e., right on top of each other. Carry out this reasoning for the case of (1) a positive charge and a negative charge of equal magnitude, (2) two positive charges of equal magnitude, (3) the gravitational energy of two equal masses.
22.4 Calculating energy in fields by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.