21.9 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
charge — a numerical rating of how strongly an object participates in electrical forces
coulomb (C) — the unit of electrical charge
current — the rate at which charge crosses a certain boundary
ampere — the metric unit of current, one coulomb per second; also “amp”
ammeter — a device for measuring electrical current
circuit — an electrical device in which charge can come back to its starting point and be recycled rather than getting stuck in a dead end
open circuit — a circuit that does not function because it has a gap in it
short circuit — a circuit that does not function because charge is given a low-resistance “shortcut” path that it can follow, instead of the path that makes it do something useful
voltage — electrical potential energy per unit charge that will be possessed by a charged particle at a certain point in space
volt — the metric unit of voltage, one joule per coulomb
voltmeter — a device for measuring voltage differences
ohmic — describes a substance in which the flow of current between two points is proportional to the voltage difference between them
resistance — the ratio of the voltage difference to the current in an object made of an ohmic substance
ohm — the metric unit of electrical resistance, one volt per ampere
Notation
`q` — charge
`I` — current
`A` — units of amperes
`V` — voltage
`V` — units of volts
`R` — resistance
`Omega` — units of ohms
Other Notation
electric potential — rather than the more informal “voltage” used here; despite the misleading name, it is not the same as electric potential energy
eV — a unit of energy, equal to `e` multiplied by 1 volt; `1.6×10^(-19)` joules
Summary
All the forces we encounter in everyday life boil down to two basic types: gravitational forces and electrical forces. A force such as friction or a “sticky force” arises from electrical forces between individual atoms.
Just as we use the word “mass” to describe how strongly an object participates in gravitational forces, we use the word “charge” for the intensity of its electrical forces. There are two types of charge. Two charges of the same type repel each other, but objects whose charges are different attract each other. Charge is measured in units of coulombs (C).
Mobile charged particle model: A great many phenomena are easily understood if we imagine matter as containing two types of charged particles, which are at least partially able to move around.
Positive and negative charge: Ordinary objects that have not been specially prepared have both types of charge spread evenly throughout them in equal amounts. The object will then tend not to exert electrical forces on any other object, since any attraction due to one type of charge will be balanced by an equal repulsion from the other. (We say “tend not to” because bringing the object near an object with unbalanced amounts of charge could cause its charges to separate from each other, and the force would no longer cancel due to the unequal distances.) It therefore makes sense to describe the two types of charge using positive and negative signs, so that an unprepared object will have zero total charge.
The Coulomb force law states that the magnitude of the electrical force between two charged particles is given by Coulomb's Law .
Conservation of charge: An even more fundamental reason for using positive and negative signs for charge is that with this definition the total charge of a closed system is a conserved quantity.
All electrical phenomena are alike in that that arise from the presence or motion of charge. Most practical electrical devices are based on the motion of charge around a complete circuit, so that the charge can be recycled and does not hit any dead ends. The most useful measure of the flow of charge is current, `I=(Deltaq)/(Deltat)`.
An electrical device whose job is to transform energy from one form into another, e.g., a lightbulb, uses power at a rate which depends both on how rapidly charge is flowing through it and on how much work is done on each unit of charge. The latter quantity is known as the voltage difference between the point where the current enters the device and the point where the current leaves it. Since there is a type of potential energy associated with electrical forces, the amount of work they do is equal to the difference in potential energy between the two points, and we therefore define voltage differences directly in terms of potential energy, `DeltaV=(DeltaPE_"elec")/q`. The rate of power dissipation is `P=IDeltaV`.
Many important electrical phenomena can only be explained if we understand the mechanisms of current flow at the atomic level. In metals, currents are carried by electrons, in liquids by ions. Gases are normally poor conductors unless their atoms are subjected to such intense electrical forces that the atoms become ionized.
Many substances, including all solids, respond to electrical forces in such a way that the flow of current between two points is proportional to the voltage difference between those points. Such a substance is called ohmic, and an object made out of an ohmic substance can be rated in terms of its resistance, `R=(DeltaV)/I`. An important corollary is that a perfect conductor, with `R=0`, must have constant voltage everywhere within it.
A schematic is a drawing of a circuit that standardizes and stylizes its features to make it easier to understand. Any circuit can be broken down into smaller parts. For instance, one big circuit may be understood as two small circuits in series, another as three circuits in parallel. When circuit elements are combined in parallel and in series, we have two basic rules to guide us in understanding how the parts function as a whole:
the junction rule: In any circuit that is not storing or releasing charge, conservation of charge implies that the total current flowing out of any junction must be the same as the total flowing in.
the loop rule: Assuming the standard convention for plus and minus signs, the sum of the voltage drops around any closed loop in a circuit must be zero.
The simplest application of these rules is to pairs of resistors combined in series or parallel. In such cases, the pair of resistors acts just like a single unit with a certain resistance value, called their equivalent resistance. Resistances in series add to produce a larger equivalent resistance,
`R_"series"=R_1+R_2,`
because the current has to fight its way through both resistances. Parallel resistors combine to produce an equivalent resistance that is smaller than either individual resistance,
`R_"parallel"=``(1/R_1+1/R_2)^(-1)`
because the current has two different paths open to it.
An important example of resistances in parallel and series is the use of voltmeters and ammeters in resistive circuits. A voltmeter acts as a large resistance in parallel with the resistor across which the voltage drop is being measured. The fact that its resistance is not infinite means that it alters the circuit it is being used to investigate, producing a lower equivalent resistance. An ammeter acts as a small resistance in series with the circuit through which the current is to be determined. Its resistance is not quite zero, which leads to an increase in the resistance of the circuit being tested.
Homework Problems
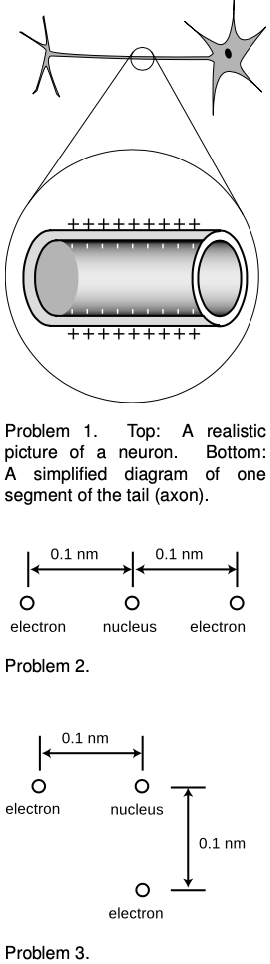 1. The figure shows a neuron, which is the type of cell your nerves are made of. Neurons serve to transmit sensory information to the brain, and commands from the brain to the muscles. All this data is transmitted electrically, but even when the cell is resting and not transmitting any information, there is a layer of negative electrical charge on the inside of the cell membrane, and a layer of positive charge just outside it. This charge is in the form of various ions dissolved in the interior and exterior fluids. Why would the negative charge remain plastered against the inside surface of the membrane, and likewise why doesn't the positive charge wander away from the outside surface?
1. The figure shows a neuron, which is the type of cell your nerves are made of. Neurons serve to transmit sensory information to the brain, and commands from the brain to the muscles. All this data is transmitted electrically, but even when the cell is resting and not transmitting any information, there is a layer of negative electrical charge on the inside of the cell membrane, and a layer of positive charge just outside it. This charge is in the form of various ions dissolved in the interior and exterior fluids. Why would the negative charge remain plastered against the inside surface of the membrane, and likewise why doesn't the positive charge wander away from the outside surface?
2. A helium atom finds itself momentarily in this arrangement. Find the direction and magnitude of the force acting on the right-hand electron. The two protons in the nucleus are so close together (~11 fm) that you can consider them as being right on top of each other. As discussed in chapter 26, the charge of an electron is `-e`, and the charge of a proton `e`, where `e=1.60×10^(-19) C`. `sqrt`
3. The helium atom of problem 2 has some new experiences, goes through some life changes, and later on finds itself in the configuration shown here. What are the direction and magnitude of the force acting on the bottom electron? (Draw a sketch to make clear the definition you are using for the angle that gives direction.) `sqrt`
4. [See ch. 1 for help on how to do order-of-magnitude estimates.] Suppose you are holding your hands in front of you, `10` cm apart.
(a) Estimate the total number of electrons in each hand.
(b) Estimate the total repulsive force of all the electrons in one hand on all the electrons in the other.
(c) Why don't you feel your hands repelling each other?
(d) Estimate how much the charge of a proton could differ in magnitude from the charge of an electron without creating a noticeable force between your hands.
5. Suppose that a proton in a lead nucleus wanders out to the surface of the nucleus, and experiences a strong nuclear force of about `8` kN from the nearby neutrons and protons pulling it back in. Compare this numerically to the repulsive electrical force from the other protons, and verify that the net force is attractive. A lead nucleus is very nearly spherical, is about `6.5` fm in radius, and contains `82` protons, each with a charge of `+e`, where `e=1.60×10^(-19) C`. `sqrt`
6. The subatomic particles called muons behave exactly like electrons, except that a muon's mass is greater by a factor of `206.77`. Muons are continually bombarding the Earth as part of the stream of particles from space known as cosmic rays. When a muon strikes an atom, it can displace one of its electrons. If the atom happens to be a hydrogen atom, then the muon takes up an orbit that is on the average `206.77` times closer to the proton than the orbit of the ejected electron. How many times greater is the electric force experienced by the muon than that previously felt by the electron? `sqrt`
7. The Earth and Moon are bound together by gravity. If, instead, the force of attraction were the result of each having a charge of the same magnitude but opposite in sign, find the quantity of charge that would have to be placed on each to produce the required force. `sqrt`
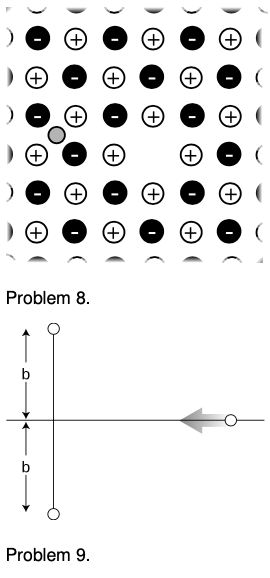 8. The figure shows one layer of the three-dimensional structure of a salt crystal. The atoms extend much farther off in all directions, but only a six-by-six square is shown here. The larger circles are the chlorine ions, which have charges of `-e`, where `e=1.60×10^(-19) C`. The smaller circles are sodium ions, with charges of `+e`. The center-to-center distance between neighboring ions is about `0.3` nm. Real crystals are never perfect, and the crystal shown here has two defects: a missing atom at one location, and an extra lithium atom, shown as a grey circle, inserted in one of the small gaps. If the lithium atom has a charge of `+e`, what is the direction and magnitude of the total force on it? Assume there are no other defects nearby in the crystal besides the two shown here. [Hints: The force on the lithium ion is the vector sum of all the forces of all the quadrillions of sodium and chlorine atoms, which would obviously be too laborious to calculate. Nearly all of these forces, however, are canceled by a force from an ion on the opposite side of the lithium.] `sqrt``***`
8. The figure shows one layer of the three-dimensional structure of a salt crystal. The atoms extend much farther off in all directions, but only a six-by-six square is shown here. The larger circles are the chlorine ions, which have charges of `-e`, where `e=1.60×10^(-19) C`. The smaller circles are sodium ions, with charges of `+e`. The center-to-center distance between neighboring ions is about `0.3` nm. Real crystals are never perfect, and the crystal shown here has two defects: a missing atom at one location, and an extra lithium atom, shown as a grey circle, inserted in one of the small gaps. If the lithium atom has a charge of `+e`, what is the direction and magnitude of the total force on it? Assume there are no other defects nearby in the crystal besides the two shown here. [Hints: The force on the lithium ion is the vector sum of all the forces of all the quadrillions of sodium and chlorine atoms, which would obviously be too laborious to calculate. Nearly all of these forces, however, are canceled by a force from an ion on the opposite side of the lithium.] `sqrt``***`
9. In the semifinals of an electrostatic croquet tournament, Jessica hits her positively charged ball, sending it across the playing field, rolling to the left along the `x` axis. It is repelled by two other positive charges. These two equal charges are fixed on the `y` axis at the locations shown in the figure. (a) Express the force on the ball in terms of the ball's position, `x`. (b) At what value of `x` does the ball experience the greatest deceleration? Express you answer in terms of `b`. [Based on a problem by Halliday and Resnick.] `sqrt`
10. (solution in the pdf version of the book) In a wire carrying a current of 1.0 pA, how long do you have to wait, on the average, for the next electron to pass a given point? Express your answer in units of microseconds. The charge of an electron is `-e=-1.60×10^(-19) C`. `sqrt`
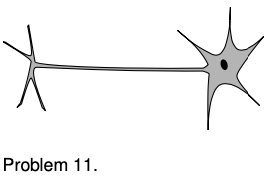 11. Referring back to our old friend the neuron from problem 1 on page 601, let's now consider what happens when the nerve is stimulated to transmit information. When the blob at the top (the cell body) is stimulated, it causes Na+ ions to rush into the top of the tail (axon). This electrical pulse will then travel down the axon, like a flame burning down from the end of a fuse, with the `Na+` ions at each point first going out and then coming back in. If `10^10 "Na"^+` ions cross the cell membrane in `0.5` ms, what amount of current is created? The charge of a `"Na"^+` ion is `+e=1.60×10^(-19) C`. `sqrt`
11. Referring back to our old friend the neuron from problem 1 on page 601, let's now consider what happens when the nerve is stimulated to transmit information. When the blob at the top (the cell body) is stimulated, it causes Na+ ions to rush into the top of the tail (axon). This electrical pulse will then travel down the axon, like a flame burning down from the end of a fuse, with the `Na+` ions at each point first going out and then coming back in. If `10^10 "Na"^+` ions cross the cell membrane in `0.5` ms, what amount of current is created? The charge of a `"Na"^+` ion is `+e=1.60×10^(-19) C`. `sqrt`
12. If a typical light bulb draws about 900 mA from a 110-V household circuit, what is its resistance? (Don't worry about the fact that it's alternating current.) `sqrt`
13. A resistor has a voltage difference `DeltaV` across it, causing a current `I` to flow.
(a) Find an equation for the power it dissipates as heat in terms of the variables `I` and `R` only, eliminating `DeltaV`. `sqrt`
(b) If an electrical line coming to your house is to carry a given amount of current, interpret your equation from part a to explain whether the wire's resistance should be small, or large.
14. (a) Express the power dissipated by a resistor in terms of `R` and `DeltaV` only, eliminating II. `sqrt`
(b) Electrical receptacles in your home are mostly `110` V, but circuits for electric stoves, air conditioners, and washers and driers are usually `220` V. The two types of circuits have differently shaped receptacles. Suppose you rewire the plug of a drier so that it can be plugged in to a `110` V receptacle. The resistor that forms the heating element of the drier would normally draw `200` W. How much power does it actually draw now? `sqrt`
 15. Use the result of problem 42 on page 608 to find an equation for the voltage at a point in space at a distance `r` from a point charge `Q`. (Take your `V=0` distance to be anywhere you like.) `sqrt`
15. Use the result of problem 42 on page 608 to find an equation for the voltage at a point in space at a distance `r` from a point charge `Q`. (Take your `V=0` distance to be anywhere you like.) `sqrt`
16. You are given a battery, a flashlight bulb, and a single piece of wire. Draw at least two configurations of these items that would result in lighting up the bulb, and at least two that would not light it. (Don't draw schematics.) If you're not sure what's going on, borrow the materials from your instructor and try it. Note that the bulb has two electrical contacts: one is the threaded metal jacket, and the other is the tip (at the bottom in the figure). [Problem by Arnold Arons.]
17. (solution in the pdf version of the book) You have to do different things with a circuit to measure current than to measure a voltage difference. Which would be more practical for a printed circuit board, in which the wires are actually strips of metal inlaid on the surface of the board?
18. Problem 18 has been replaced with problem 43.
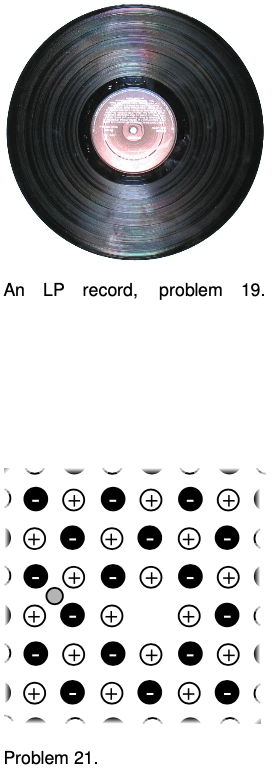 19. (a) You take an LP record out of its sleeve, and it acquires a static charge of `1` nC. You play it at the normal speed of `33 1/3` r.p.m., and the charge moving in a circle creates an electric current. What is the current, in amperes? `sqrt`
19. (a) You take an LP record out of its sleeve, and it acquires a static charge of `1` nC. You play it at the normal speed of `33 1/3` r.p.m., and the charge moving in a circle creates an electric current. What is the current, in amperes? `sqrt`
(b) Although the planetary model of the atom can be made to work with any value for the radius of the electrons' orbits, more advanced models that we will study later in this course predict definite radii. If the electron is imagined as circling around the proton at a speed of `2.2×10^6 m"/"s`, in an orbit with a radius of `0.05` nm, what electric current is created? The charge of an electron is `-e=-1.60×10^(-19) C`. `sqrt`
20. Three charges, each of strength `Q (Q>0)` form a fixed equilateral triangle with sides of length `b`. You throw a particle of mass mmand positive charge `q` from far away, with an initial speed `v`. Your goal is to get the particle to go to the center of the triangle, your aim is perfect, and you are free to throw from any direction you like. What is the minimum possible value of `v`? You will need the result of problem 42. `sqrt``***`
21. Referring back to problem 8 on page 602 about the sodium chloride crystal, suppose the lithium ion is going to jump from the gap it is occupying to one of the four closest neighboring gaps. Which one will it jump to, and if it starts from rest, how fast will it be going by the time it gets there? (It will keep on moving and accelerating after that, but that does not concern us.) You will need the result of problem 42. `sqrt``***`
22. We have referred to resistors dissipating heat, i.e., we have assumed that `P=IDeltaV` is always greater than zero. Could `IDeltaV` come out to be negative for a resistor? If so, could one make a refrigerator by hooking up a resistor in such a way that it absorbed heat instead of dissipating it?
23. Today, even a big luxury car like a Cadillac can have an electrical system that is relatively low in power, since it doesn't need to do much more than run headlights, power windows, etc. In the near future, however, manufacturers plan to start making cars with electrical systems about five times more powerful. This will allow certain energy-wasting parts like the water pump to be run on electrical motors and turned off when they're not needed --- currently they're run directly on shafts from the motor, so they can't be shut off. It may even be possible to make an engine that can shut off at a stoplight and then turn back on again without cranking, since the valves can be electrically powered. Current cars' electrical systems have `12`-volt batteries (with `14`-volt chargers), but the new systems will have `36`-volt batteries (with `42`-volt chargers).
(a) Suppose the battery in a new car is used to run a device that requires the same amount of power as the corresponding device in the old car. Based on the sample figures above, how would the currents handled by the wires in one of the new cars compare with the currents in the old ones?
(b) The real purpose of the greater voltage is to handle devices that need more power. Can you guess why they decided to change to `36`-volt batteries rather than increasing the power without increasing the voltage? `sqrt`
24. (a) Many battery-operated devices take more than one battery. If you look closely in the battery compartment, you will see that the batteries are wired in series. Consider a flashlight circuit. What does the loop rule tell you about the effect of putting several batteries in series in this way?
(b) The cells of an electric eel's nervous system are not that different from ours --- each cell can develop a voltage difference across it of somewhere on the order of one volt. How, then, do you think an electric eel can create voltages of thousands of volts between different parts of its body?
25. The heating element of an electric stove is connected in series with a switch that opens and closes many times per second. When you turn the knob up for more power, the fraction of the time that the switch is closed increases. Suppose someone suggests a simpler alternative for controlling the power by putting the heating element in series with a variable resistor controlled by the knob. (With the knob turned all the way clockwise, the variable resistor's resistance is nearly zero, and when it's all the way counterclockwise, its resistance is essentially infinite.) (a) Draw schematics. (b) Why would the simpler design be undesirable?
26. A `1.0` `Omega` toaster and a `2.0` `Omega` lamp are connected in parallel with the `110`-V supply of your house. (Ignore the fact that the voltage is AC rather than DC.)
(a) Draw a schematic of the circuit.
(b) For each of the three components in the circuit, find the current passing through it and the voltage drop across it. `sqrt`
(c) Suppose they were instead hooked up in series. Draw a schematic and calculate the same things. `sqrt`
27. Wire is sold in a series of standard diameters, called “gauges.” The difference in diameter between one gauge and the next in the series is about `20%`. How would the resistance of a given length of wire compare with the resistance of the same length of wire in the next gauge in the series? `sqrt`
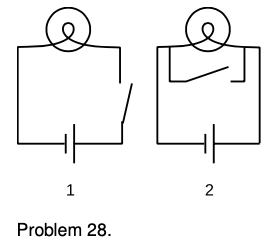
28. The figure shows two possible ways of wiring a flashlight with a switch. Both will serve to turn the bulb on and off, although the switch functions in the opposite sense. Why is method `1` preferable?
29. In the figure, the battery is `9` V.
(a) What are the voltage differences across each light bulb? `sqrt`
(b) What current flows through each of the three components of the circuit? `sqrt`
(c) If a new wire is added to connect points `A` and `B`, how will the appearances 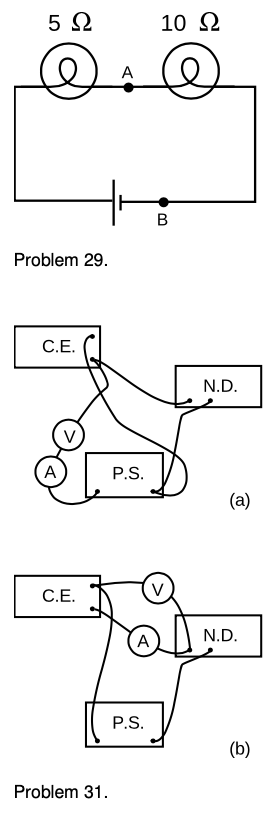 of the bulbs change? What will be the new voltages and currents?
of the bulbs change? What will be the new voltages and currents?
(d) Suppose no wire is connected from `A` to `B`, but the two bulbs are switched. How will the results compare with the results from the original setup as drawn?
30. You have a circuit consisting of two unknown resistors in series, and a second circuit consisting of two unknown resistors in parallel.
(a) What, if anything, would you learn about the resistors in the series circuit by finding that the currents through them were equal?
(b) What if you found out the voltage differences across the resistors in the series circuit were equal?
(c) What would you learn about the resistors in the parallel circuit from knowing that the currents were equal?
(d) What if the voltages in the parallel circuit were equal?
31. A student in a biology lab is given the following instructions: “Connect the cerebral eraser (C.E.) and the neural depolarizer (N.D.) in parallel with the power supply (P.S.). (Under no circumstances should you ever allow the cerebral eraser to come within `20` cm of your head.) Connect a voltmeter to measure the voltage across the cerebral eraser, and also insert an ammeter in the circuit so that you can make sure you don't put more than `100` mA through the neural depolarizer.” The diagrams show two lab groups' attempts to follow the instructions. (a) Translate diagram a into a standard-style schematic. What is correct and incorrect about this group's setup? (b) Do the same for diagram b.
32. How many different resistance values can be created by combining three unequal resistors? (Don't count possibilities where not all the resistors are used.)
33. A person in a rural area who has no electricity runs an extremely long extension cord to a friend's house down the road so she can run an electric light. The cord is so long that its resistance, `x`, is not negligible. Show that the lamp's brightness is greatest if its resistance, `y`, is equal to `x`. Explain physically why the lamp is dim for values of `y` that are too small or too large. `int`
34. What resistance values can be created by combining a `1 kOmega` resistor and a `10 kOmega` resistor? (solution in the pdf version of the book)
35. Suppose six identical resistors, each with resistance `R`, are connected so that they form the edges of a tetrahedron (a pyramid with three sides in addition to the base, i.e., one less side than an Egyptian pyramid). What resistance value or values can be obtained by making connections onto any two points on this arrangement? (solution in the pdf version of the book)`***`
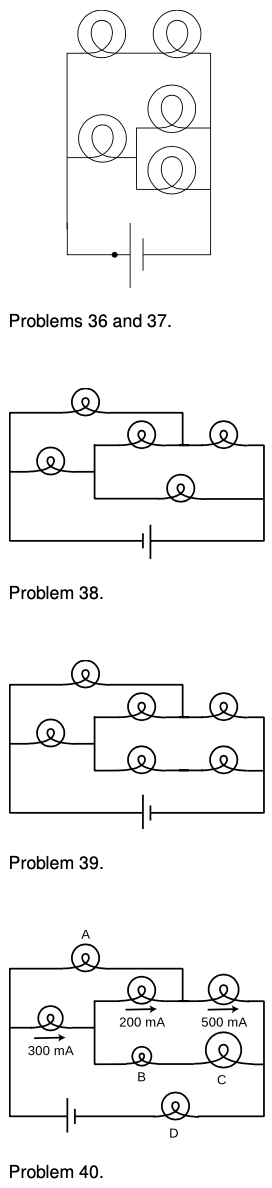 36. The figure shows a circuit containing five lightbulbs connected to a battery. Suppose you're going to connect one probe of a voltmeter to the circuit at the point marked with a dot. How many unique, nonzero voltage differences could you measure by connecting the other probe to other wires in the circuit?
36. The figure shows a circuit containing five lightbulbs connected to a battery. Suppose you're going to connect one probe of a voltmeter to the circuit at the point marked with a dot. How many unique, nonzero voltage differences could you measure by connecting the other probe to other wires in the circuit?
37. The lightbulbs in the figure are all identical. If you were inserting an ammeter at various places in the circuit, how many unique currents could you measure? If you know that the current measurement will give the same number in more than one place, only count that as one unique current.
38. The bulbs are all identical. Which one doesn't light up?`***`
39. Each bulb has a resistance of one ohm. How much power is drawn from the one-volt battery? `sqrt``***`
40. The bulbs all have unequal resistances. Given the three currents shown in the figure, find the currents through bulbs `A`, `B`, `C`, and `D`.
41. A silk thread is uniformly charged by rubbing it with llama fur. The thread is then dangled vertically above a metal plate and released. As each part of the thread makes contact with the conducting plate, its charge is deposited onto the plate. Since the thread is accelerating due to gravity, the rate of charge deposition increases with time, and by time `t` the cumulative amount of charge is , where `c` is a constant. (a) Find the current flowing onto the plate. `sqrt`
(b) Suppose that the charge is immediately carried away through a resistance `R`. Find the power dissipated as heat. `sqrt``int`
(b) Electrical forces are closely analogous to gravitational ones, since both depend on `1"/"r^2`. Since the forces are analogous, the potential energies should also behave analogously. Using this analogy, write down the expression for the electrical potential energy of two interacting charged particles. The main uncertainty here is the sign out in front. Like masses attract, but like charges repel. To figure out whether you have the right sign in your equation, sketch graphs in the case where both charges are positive, and also in the case where one is positive and one negative; make sure that in both cases, when the charges are released near one another, their motion causes them to lose PE while gaining KE. `sqrt`
43. In example 8 on p. 580, suppose that the larger sphere has radius `a`, the smaller one `b`. (a) Use the result of problem 15 show that the ratio of the charges on the two spheres is `q_a"/"q_b=a"/"b`. (b) Show that the density of charge (charge per unit area) is the other way around: the charge density on the smaller sphere is greater than that on the larger sphere in the ratio `a"/"b`.
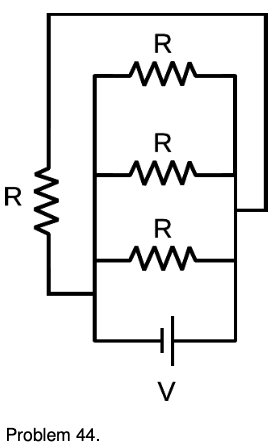
44. Find the current drawn from the battery. `sqrt`
Exercise 21A: Electrical measurements
1. How many different currents could you measure in this circuit? Make a prediction, and then try it.

What do you notice? How does this make sense in terms of the roller coaster metaphor introduced in discussion question 21.5B on p. 226?
What is being used up in the resistor?
2. By connecting probes to these points, how many ways could you measure a voltage? How many of them would be different numbers? Make a prediction, and then do it.

What do you notice? Interpret this using the roller coaster metaphor, and color in parts of the circuit that represent constant voltages.
3. The resistors are unequal. How many different voltages and currents can you measure? Make a prediction, and then try it.

What do you notice? Interpret this using the roller coaster metaphor, and color in parts of the circuit that represent constant voltages.
Exercise 21B: Voltage and current
This exercise is based on one created by Virginia Roundy.
Apparatus:
- DC power supply
- 1.5 volt batteries
- lightbulbs and holders
- wire
- highlighting pens, 3 colors
When you first glance at this exercise, it may look scary and intimidating --- all those circuits! However, all those wild-looking circuits can be analyzed using the following four guides to thinking:
1. A circuit has to be complete , i.e., it must be possible for charge to get recycled as it goes around the circuit. If it's not complete, then charge will build up at a dead end. This built-up charge will repel any other charge that tries to get in, and everything will rapidly grind to a stop.
2. There is constant voltage everywhere along a piece of wire. To apply this rule during this lab, I suggest you use the colored highlighting pens to mark the circuit. For instance, if there's one whole piece of the circuit that's all at the same voltage, you could highlight it in yellow. A second piece of the circuit, at some other voltage, could be highlighted in blue.
3. Charge is conserved, so charge can't “get used up.”
4. You can draw a rollercoaster diagram, like the one shown below. On this kind of diagram, height corresponds to voltage --- that's why the wires are drawn as horizontal tracks.

A Bulb and a Switch
Look at circuit 1, and try to predict what will happen when the switch is open, and what will happen when it's closed. Write both your predictions in the table on the following page before you build the circuit. When you build the circuit, you don't need an actual switch like a light switch; just connect and disconnect the banana plugs. Use one of the 1.5 volt batteries as your voltage source.
| color | meaning |
| black | 0 |
| brown | 1 |
| red | 2 |
| orange | 3 |
| yellow | 4 |
| green | 5 |
| blue | 6 |
| violet | 7 |
| gray | 8 |
| white | 9 |
| silver | ±10% |
| gold | ±5% |

* Circuit 1 {switch open}{ switch closed}
Did it work the way you expected? If not, try to figure it out with the benefit of hindsight, and write your explanation in the table above.

* Circuit 2 (Don't leave the switch closed for a long time!)}
{switch open}{switch closed}

* Circuit 3
{switch open}{switch closed}

*{Circuit 4}
{switch open}{switch closed}
Two Bulbs
Instead of a battery, use the DC power supply, set to 2.4 volts, for circuits 5 and 6. Analyze this one both by highlighting and by drawing a rollercoaster diagram.

* {Circuit 5}
{bulb a}{bulb b}

*{Circuit 6}
{bulb a}{bulb b}
Two Batteries
Use batteries for circuits 7-9. Circuits 7 and 8 are both good candidates for rollercoaster diagrams.

* {Circuit 7}

* {Circuit 8}
A Final Challenge

* {Circuit 9}
{bulb a}{bulb b}
Exercise 21C: Reasoning about circuits
The questions in this exercise can all be solved using some combination of the following approaches:
a) There is constant voltage throughout any conductor.
b) Ohm's law can be applied to any part of a circuit.
c) Apply the loop rule.
d) Apply the junction rule.
In each case, discuss the question, decide what you think is the right answer, and then try the experiment.
If you've already done exercise 21B, skip number 1.
1. The series circuit is changed as shown.

Which reasoning is correct?
- Each bulb now has its sides connected to the two terminals of the battery, so each now has 2.4 V across it instead of 1.2 V. They get brighter.
- Just as in the original circuit, the current goes through one bulb, then the other. It's just that now the current goes in a figure-8 pattern. The bulbs glow the same as before.
2. A wire is added as shown to the original circuit.

What is wrong with the following reasoning?
The top right bulb will go out, because its two sides are now connected with wire, so there will be no voltage difference across it. The other three bulbs will not be affected.
3. A wire is added as shown to the original circuit.

What is wrong with the following reasoning?
The current flows out of the right side of the battery. When it hits the first junction, some of it will go left and some will keep going up The part that goes up lights the top right bulb. The part that turns left then follows the path of least resistance, going through the new wire instead of the bottom bulb. The top bulb stays lit, the bottom one goes out, and others stay the same.
4. What happens when one bulb is unscrewed, leaving an air gap?

5. This part is optional. You can do it if you finished early and would like an extra challenge.
Predict the voltage drop across each of the three bulbs in part 4, and also predict how the three currents will compare with one another. (You can't predict the currents in units of amperes, since you don't know the resistances of the bulbs.) Test your predictions. If your predictions are wrong, try to figure out what's going on.
21.9 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.