21.3 Current by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
21.3 Current
Unity of all types of electricity
We are surrounded by things we have been told are “electrical,” but it's far from obvious what they have in common to justify being grouped together. What relationship is there between the way socks cling together and the way a battery lights a lightbulb? We have been told that both an electric eel and our own brains are somehow electrical in nature, but what do they have in common?
British physicist Michael Faraday (1791-1867) set out to address this problem. He investigated electricity from a variety of sources --- including electric eels! --- to see whether they could all produce the same effects, such as shocks and sparks, attraction and repulsion. “Heating” refers, for example, to the way a lightbulb filament gets hot enough to glow and emit light. Magnetic induction is an effect discovered by Faraday himself that connects electricity and magnetism. We will not study this effect, which is the basis for the electric generator, in detail until later in the book.
| source | effect | |||
| shocks | sparks | attraction and repulsion | heating | |
| rubbing | `sqrt` | `sqrt` | `sqrt` | `sqrt` |
| battery | `sqrt` | `sqrt` | `sqrt` | `sqrt` |
| animal | `sqrt` | `sqrt` | (`sqrt`) | `sqrt` |
| magnetically induced | `sqrt` | `sqrt` | `sqrt` | `sqrt` |
 The table shows a summary of some of Faraday's results. Check marks indicate that Faraday or his close contemporaries were able to verify that a particular source of electricity was capable of producing a certain effect. (They evidently failed to demonstrate attraction and repulsion between objects charged by electric eels, although modern workers have studied these species in detail and been able to understand all their electrical characteristics on the same footing as other forms of electricity.)
The table shows a summary of some of Faraday's results. Check marks indicate that Faraday or his close contemporaries were able to verify that a particular source of electricity was capable of producing a certain effect. (They evidently failed to demonstrate attraction and repulsion between objects charged by electric eels, although modern workers have studied these species in detail and been able to understand all their electrical characteristics on the same footing as other forms of electricity.)
Faraday's results indicate that there is nothing fundamentally different about the types of electricity supplied by the various sources. They are all able to produce a wide variety of identical effects. Wrote Faraday, “The general conclusion which must be drawn from this collection of facts is that electricity, whatever may be its source, is identical in its nature.”
If the types of electricity are the same thing, what thing is that? The answer is provided by the fact that all the sources of electricity can cause objects to repel or attract each other. We use the word “charge” to describe the property of an object that allows it to participate in such electrical forces, and we have learned that charge is present in matter in the form of nuclei and electrons. Evidently all these electrical phenomena boil down to the motion of charged particles in matter.
Electric current
If the fundamental phenomenon is the motion of charged particles, then how can we define a useful numerical measurement of it? We might describe the flow of a river simply by the velocity of the water, but velocity will not be appropriate for electrical purposes because we need to take into account how much charge the moving particles have, and in any case there are no practical devices sold at Radio Shack that can tell us the velocity of charged particles. Experiments show that the intensity of various electrical effects is related to a different quantity: the number of coulombs of charge that pass by a certain point per second. By analogy with the flow of water, this quantity is called the electric current, `I`. Its units of coulombs/second are more conveniently abbreviated as amperes, `1 A=1 C/s`. (In informal speech, one usually says “amps.”)
 The main subtlety involved in this definition is how to account for the two types of charge. The stream of water coming from a hose is made of atoms containing charged particles, but it produces none of the effects we associate with electric currents. For example, you do not get an electrical shock when you are sprayed by a hose. This type of experiment shows that the effect created by the motion of one type of charged particle can be canceled out by the motion of the opposite type of charge in the same direction. In water, every oxygen atom with a charge of `+8e` is surrounded by eight electrons with charges of `-e`, and likewise for the hydrogen atoms.
The main subtlety involved in this definition is how to account for the two types of charge. The stream of water coming from a hose is made of atoms containing charged particles, but it produces none of the effects we associate with electric currents. For example, you do not get an electrical shock when you are sprayed by a hose. This type of experiment shows that the effect created by the motion of one type of charged particle can be canceled out by the motion of the opposite type of charge in the same direction. In water, every oxygen atom with a charge of `+8e` is surrounded by eight electrons with charges of `-e`, and likewise for the hydrogen atoms.
We therefore refine our definition of current as follows:
definition of electric current
When charged particles are exchanged between regions of space A and B, the electric current flowing from A to B is
where `Deltaq` is the change in region B's total charge occurring over a period of time `Deltat`.
In the garden hose example, your body picks up equal amounts of positive and negative charge, resulting in no change in your total charge, so the electrical current flowing into you is zero.
Example 1: Interpretation of `Deltaq"/"Deltat`
`=>` How should the expression `Deltaq"/"Deltat` be interpreted when the current isn't constant?
`=>` You've seen lots of equations of this form before: `v=(Deltax)/(Deltat)`, `F=(Deltap)/(Deltat)`, etc. These are all descriptions of rates of change, and they all require that the rate of change be constant. If the rate of change isn't constant, you instead have to use the slope of the tangent line on a graph. The slope of a tangent line is equivalent to a derivative in calculus; applications of calculus are discussed in section 21.7.
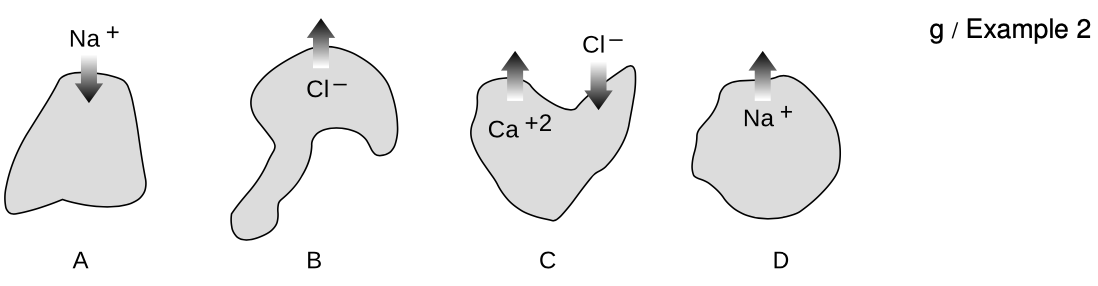
Example 2: Ions moving across a cell membrane
`=>` Figure g shows ions, labeled with their charges, moving in or out through the membranes of four cells. If the ions all cross the membranes during the same interval of time, how would the currents into the cells compare with each other?
`=>` Cell A has positive current going into it because its charge is increased, i.e., has a positive value of `Deltaq`.
Cell B has the same current as cell A, because by losing one unit of negative charge it also ends up increasing its own total charge by one unit.
Cell C's total charge is reduced by three units, so it has a large negative current going into it.
Cell D loses one unit of charge, so it has a small negative current into it.
It may seem strange to say that a negatively charged particle going one way creates a current going the other way, but this is quite ordinary. As we will see, currents flow through metal wires via the motion of electrons, which are negatively charged, so the direction of motion of the electrons in a circuit is always opposite to the direction of the current. Of course it would have been convenient of Benjamin Franklin had defined the positive and negative signs of charge the opposite way, since so many electrical devices are based on metal wires.
Example 3: Number of electrons flowing through a lightbulb
`=>` If a lightbulb has 1.0 A flowing through it, how many electrons will pass through the filament in 1.0 s?
`=>` We are only calculating the number of electrons that flow, so we can ignore the positive and negative signs. Solving for `Deltaq=IDeltat` gives a charge of 1.0 C flowing in this time interval. The number of electrons is
`"number of electrons"="coulombs"×"electrons"/"coulomb"`
`="coulombs""/""coulombs"/"electron"`
`=1.0 C"/"e`
`=6.2×10^18`
21.3 Current by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.