19.2 Waves on a string by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
19.2 Waves on a string
 The result is a pair of pulses moving away from the point of impact.
The result is a pair of pulses moving away from the point of impact.
So far you have learned some counterintuitive things about the behavior of waves, but intuition can be trained. The first half of this section aims to build your intuition by investigating a simple, one-dimensional type of wave: a wave on a string. If you have ever stretched a string between the bottoms of two open-mouthed cans to talk to a friend, you were putting this type of wave to work. Stringed instruments are another good example. Although we usually think of a piano wire simply as vibrating, the hammer actually strikes it quickly and makes a dent in it, which then ripples out in both directions. Since this chapter is about free waves, not bounded ones, we pretend that our string is infinitely long.
After the qualitative discussion, we will use simple approximations to investigate the speed of a wave pulse on a string. This quick and dirty treatment is then followed by a rigorous attack using the methods of calculus, which may be skipped by the student who has not studied calculus. How far you penetrate in this section is up to you, and depends on your mathematical self-confidence. If you skip some of the math, you should nevertheless absorb the significance of the result, discussed on p. 492.
Intuitive ideas
Consider a string that has been struck, 1/1, resulting in the creation of two wave pulses, 2, one traveling to the left and one to the right. This is analogous to the way ripples spread out in all directions from a splash in water, but on a one-dimensional string, “all directions” becomes “both directions.”
We can gain insight by modeling the string as a series of masses connected by springs. (In the actual string the mass and the springiness are both contributed by the molecules themselves.) If we look at various microscopic portions of the string, there will be some areas that are flat, m/1, some that are sloping but not curved, 2, and some that are curved, 3 and 4. In example 1 it is clear that both the forces on the central mass cancel out, so it will not accelerate. The same is true of 2, however. Only in curved regions such as 3 and 4 is an acceleration produced. In these examples, the vector sum of the two forces acting on the central mass is not zero. The important concept is that curvature makes force: the curved areas of a wave tend to experience forces resulting in an acceleration toward the mouth of the curve. Note, however, that an uncurved portion of the string need not remain motionless. It may move at constant velocity to either side.
Approximate treatment
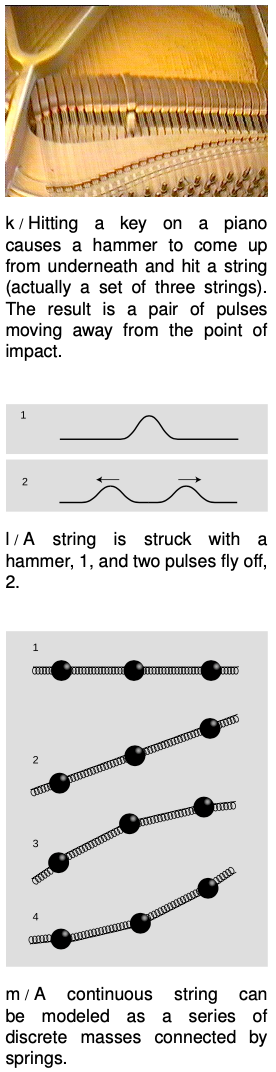
 We now carry out an approximate treatment of the speed at which two pulses will spread out from an initial indentation on a string. For simplicity, we imagine a hammer blow that creates a triangular dent, n/1. We will estimate the amount of time, `t`, required until each of the pulses has traveled a distance equal to the width of the pulse itself. The velocity of the pulses is then `±w"/"t`.
We now carry out an approximate treatment of the speed at which two pulses will spread out from an initial indentation on a string. For simplicity, we imagine a hammer blow that creates a triangular dent, n/1. We will estimate the amount of time, `t`, required until each of the pulses has traveled a distance equal to the width of the pulse itself. The velocity of the pulses is then `±w"/"t`.
As always, the velocity of a wave depends on the properties of the medium, in this case the string. The properties of the string can be summarized by two variables: the tension, `T`, and the mass per unit length, `mu`.
If we consider the part of the string encompassed by the initial dent as a single object, then this object has a mass of approximately `muw` (mass/length`*`length=mass). (Here, and throughout the derivation, we assume that `h` is much less than `w`, so that we can ignore the fact that this segment of the string has a length slightly greater than `w`. Although the downward acceleration of this segment of the string will be neither constant over time nor uniform across the string, we will pretend that it is constant for the sake of our simple estimate. Roughly speaking, the time interval between n/1 and 2 is the amount of time required for the initial dent to accelerate from rest and reach its normal, flattened position. Of course the tip of the triangle has a longer distance to travel than the edges, but again we ignore the complications and simply assume that the segment as a whole must travel a distance `h`. Indeed, it might seem surprising that the triangle would so neatly spring back to a perfectly flat shape. It is an experimental fact that it does, but our analysis is too crude to address such details.
The string is kinked, i.e., tightly curved, at the edges of the triangle, so it is here that there will be large forces that do not cancel out to zero. There are two forces acting on the triangular hump, one of magnitude `T` acting down and to the right, and one of the same magnitude acting down and to the left. If the angle of the sloping sides is `theta`, then the total force on the segment equals `2Tsintheta`. Dividing the triangle into two right triangles, we see that `sin theta` equals `h` divided by the length of one of the sloping sides. Since `h` is much less than `w`, the length of the sloping side is essentially the same as `w`/`2`, so we have `sintheta=(2h)"/"w` and `F=(4Th)"/"w`. The acceleration of the segment (actually the acceleration of its center of mass) is
`a=F/m`
`=(4Th)/(muw^2)`.
The time required to move a distance (h) under constant acceleration (a) is found by solving `h=1"/"2at^2` to yield
`t=sqrt((2h)/a)`
`=wsqrt(mu/(2T))`
Our final result for the velocity of the pulses is
`|v|=w/t`
`= sqrt((2T)/mu)`
The remarkable feature of this result is that the velocity of the pulses does not depend at all on `w` or `h`, i.e., any triangular pulse has the same speed. It is an experimental fact (and we will also prove rigorously in the following subsection) that any pulse of any kind, triangular or otherwise, travels along the string at the same speed. Of course, after so many approximations we cannot expect to have gotten all the numerical factors right. The correct result for the velocity of the pulses is `v=sqrt(T/mu)`.
The importance of the above derivation lies in the insight it brings `-` that all pulses move with the same speed `-` rather than in the details of the numerical result. The reason for our too-high value for the velocity is not hard to guess. It comes from the assumption that the acceleration was constant, when actually the total force on the segment would diminish as it flattened out.
Rigorous derivation using calculus (optional)
After expending considerable effort for an approximate solution, we now display the power of calculus with a rigorous and completely general treatment that is nevertheless much shorter and easier. Let the flat position of the string define the `x` axis, so that `y` measures how far a point on the string is from equilibrium. The motion of the string is characterized by `y(x,t)`, a function of two variables. Knowing that the force on any small segment of string depends on the curvature of the string in that area, and that the second derivative is a measure of curvature, it is not surprising to find that the infinitesimal force `dF` acting on an infinitesimal segment `dx` is given by
`dF=T(d^2y)/(dx^2)dx`.
(This can be proved by vector addition of the two infinitesimal forces acting on either side.) The acceleration is then `a=(dF)/(dm)`, or, substituting `dm=mudx`,
`(d^2y)/(dt^2)`=`T/mu(d^2y)/(dx^2)`.
The second derivative with respect to time is related to the second derivative with respect to position. This is no more than a fancy mathematical statement of the intuitive fact developed above, that the string accelerates so as to flatten out its curves.
Before even bothering to look for solutions to this equation, we note that it already proves the principle of superposition, because the derivative of a sum is the sum of the derivatives. Therefore the sum of any two solutions will also be a solution.
Based on experiment, we expect that this equation will be satisfied by any function `y(x,t)` that describes a pulse or wave pattern moving to the left or right at the correct speed `v`. In general, such a function will be of the form `y=f(x-vt)` or `y=f(x+vt)`, where `f` is any function of one variable. Because of the chain rule, each derivative with respect to time brings out a factor of `±v`. Evaluating the second derivatives on both sides of the equation gives
`(+-v)^2 f''=T/muf`.
Squaring gets rid of the sign, and we find that we have a valid solution for any function `f`, provided that `v` is given by
Significance of the result
This specific result for the speed of waves on a string, `v=sqrt(T"/"mu)`, is utterly unimportant. Don't memorize it. Don't take notes on it. Try to erase it from your memory.
What is important about this result is that it is an example of two things that are usually true, at least approximately, for mechanical waves in general:
- The speed at which a wave moves does not depend on the size or shape of the wave.
- The speed of a mechanical wave depends on a combination of two properties of the medium: some measure of its inertia and some measure of its tightness, i.e., the strength of the force trying to bring the medium back toward equilibrium.
self-check:
(a) What is it about the equation `v=sqrt(T"/"mu)` that relates to fact 1 above? (b) In the equation `v=sqrt(T"/"mu)`, which variable is a measure of inertia, and which is a measure of tightness? (c) Now suppose that we produce compressional wave pulses in a metal rod by tapping the end of the rod with a hammer. What physical properties of the rod would play the roles of inertia and tightness? How would you expect the speed of compressional waves in lead to compare with their speed in aluminum?
(answer in the back of the PDF version of the book)
19.2 Waves on a string by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.