16.2 Microscopic description of an ideal gas by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
16.3 Entropy
Efficiency and grades of energy
Some forms of energy are more convenient than others in certain situations. You can't run a spring-powered mechanical clock on a battery, and you can't run a battery-powered clock with mechanical energy. However, there is no fundamental physical principle that prevents you from converting 100% of the electrical energy in a battery into mechanical energy or vice-versa. More efficient motors and generators are being designed every year. In general, the laws of physics permit perfectly efficient conversion within a broad class of forms of energy.
Heat is different. Friction tends to convert other forms of energy into heat even in the best lubricated machines. When we slide a book on a table, friction brings it to a stop and converts all its kinetic energy into heat, but we never observe the opposite process, in which a book spontaneously converts heat energy into mechanical energy and starts moving! Roughly speaking, heat is different because it is disorganized. Scrambling an egg is easy. Unscrambling it is harder.
We summarize these observations by saying that heat is a lower grade of energy than other forms such as mechanical energy.
 Of course it is possible to convert heat into other forms of energy such as mechanical energy, and that is what a car engine does with the heat created by exploding the air-gasoline mixture. But a car engine is a tremendously inefficient device, and a great deal of the heat is simply wasted through the radiator and the exhaust. Engineers have never succeeded in creating a perfectly efficient device for converting heat energy into mechanical energy, and we now know that this is because of a deeper physical principle that is far more basic than the design of an engine.
Of course it is possible to convert heat into other forms of energy such as mechanical energy, and that is what a car engine does with the heat created by exploding the air-gasoline mixture. But a car engine is a tremendously inefficient device, and a great deal of the heat is simply wasted through the radiator and the exhaust. Engineers have never succeeded in creating a perfectly efficient device for converting heat energy into mechanical energy, and we now know that this is because of a deeper physical principle that is far more basic than the design of an engine.
Heat engines
In figure l, however, no mechanical work can be extracted because there is no difference in temperature. Although the air in l has the same total amount of energy as the air in k, the heat in l is a lower grade of energy, since none of it is accessible for doing mechanical work.
 `"efficiency"=1-Q_L/Q_H` [efficiency of any heat engine].
`"efficiency"=1-Q_L/Q_H` [efficiency of any heat engine].
It turns out that there is a particular type of heat engine, the Carnot engine, which, although not 100% efficient, is more efficient than any other. The grade of heat energy in a system can thus be unambiguously defined in terms of the amount of heat energy in it that cannot be extracted, even by a Carnot engine.
How can we build the most efficient possible engine? Let's start with an unnecessarily inefficient engine like a car engine and see how it could be improved. The radiator and exhaust expel hot gases, which is a waste of heat energy. These gases are cooler than the exploded air-gas mixture inside the cylinder, but hotter than the air that surrounds the car. We could thus improve the engine's efficiency by adding an auxiliary heat engine to it, which would operate with the first engine's exhaust as its hot reservoir and the air as its cold reservoir. In general, any heat engine that expels heat at an intermediate temperature can be made more efficient by changing it so that it expels heat only at the temperature of the cold reservoir.
Similarly, any heat engine that absorbs some energy at an intermediate temperature can be made more efficient by adding an auxiliary heat engine to it which will operate between the hot reservoir and this intermediate temperature.
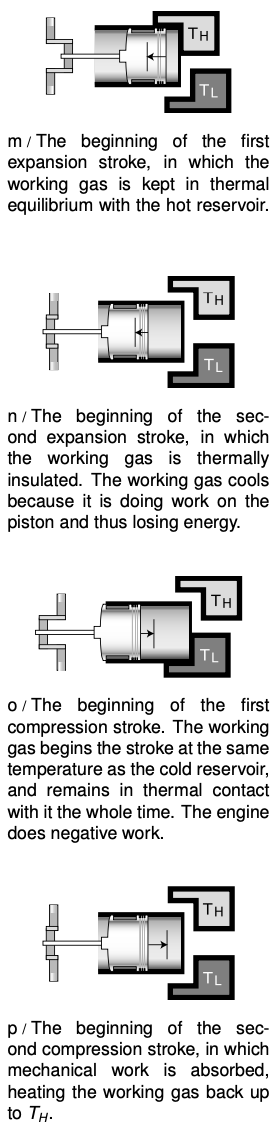
Based on these arguments, we define a Carnot engine as a heat engine that absorbs heat only from the hot reservoir and expels it only into the cold reservoir. Figures m-p show a realization of a Carnot engine using a piston in a cylinder filled with a monoatomic ideal gas. This gas, known as the working fluid, is separate from, but exchanges energy with, the hot and cold reservoirs. It turns out that this particular Carnot engine has an efficiency given by
`"efficiency"=1-T_L/T_H`, [efficiency of a Carnot engine]
where `T_L` is the temperature of the cold reservoir and `T_H` is the temperature of the hot reservoir. (A proof of this fact is given in my book Simple Nature, which you can download for free.)
Even if you do not wish to dig into the details of the proof, the basic reason for the temperature dependence is not so hard to understand. Useful mechanical work is done on strokes m and n, in which the gas expands. The motion of the piston is in the same direction as the gas's force on the piston, so positive work is done on the piston. In strokes o and p, however, the gas does negative work on the piston. We would like to avoid this negative work, but we must design the engine to perform a complete cycle. Luckily the pressures during the compression strokes are lower than the ones during the expansion strokes, so the engine doesn't undo all its work with every cycle. The ratios of the pressures are in proportion to the ratios of the temperatures, so if `T_L` is 20% of `T_H`, the engine is 80% efficient.
We have already proved that any engine that is not a Carnot engine is less than optimally efficient, and it is also true that all Carnot engines operating between a given pair of temperatures `T_H` and `T_L` have the same efficiency. Thus a Carnot engine is the most efficient possible heat engine.
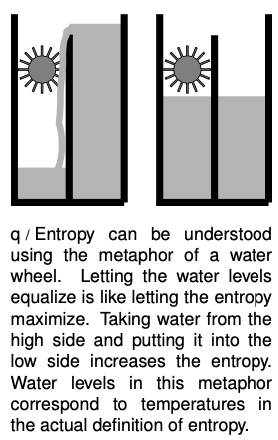 Entropy
Entropy
(1) Entropy is additive. When we combine two systems and consider them as one, the entropy of the combined system equals the sum of the entropies of the two original systems. (Quantities like mass and energy also have this property.)
(2) The entropy of a system is not changed by operating a Carnot engine within it.
It turns out to be simpler and more useful to define changes in entropy than absolute entropies. Suppose as an example that a system contains some hot matter and some cold matter. It has a relatively high grade of energy because a heat engine could be used to extract mechanical work from it. But if we allow the hot and cold parts to equilibrate at some lukewarm temperature, the grade of energy has gotten worse. Thus putting heat into a hotter area is more useful than putting it into a cold area. Motivated by these considerations, we define a change in entropy as follows:
` Delta S = Q/T` [change in entropy when adding heat `Q` to matter at temperature `T`; `DeltaS` is negative if heat is taken out]
A system with a higher grade of energy has a lower entropy.
Example 12: Entropy is additive.
Since changes in entropy are defined by an additive quantity (heat) divided by a non-additive one (temperature), entropy is additive.
Example 13: Entropy isn't changed by a Carnot engine.
The efficiency of a heat engine is defined by
and the efficiency of a Carnot engine is
so for a Carnot engine we have `Q_L"/"Q_H=T_L"/"T_H`, which can be rewritten as `Q_L"/"T_L=Q_H"/"T_H`. The entropy lost by the hot reservoir is therefore the same as the entropy gained by the cold one.
Example 14: Entropy increases in heat conduction.
When a hot object gives up energy to a cold one, conservation of energy tells us that the amount of heat lost by the hot object is the same as the amount of heat gained by the cold one. The change in entropy is `-Q"/"T_H+Q"/"T_L`, which is positive because `T_L<T_H`.
Example 15: Entropy is increased by a non-Carnot engine.
The efficiency of a non-Carnot engine is less than `1 - T_L"/"T_H`, so `Q_L"/"Q_H>T_L"/"T_H` and `Q_L"/"T_L>Q_H"/"T_H`. This means that the entropy increase in the cold reservoir is greater than the entropy decrease in the hot reservoir.
Example 16: A book sliding to a stop
A book slides across a table and comes to a stop. Once it stops, all its kinetic energy has been transformed into heat. As the book and table heat up, their entropies both increase, so the total entropy increases as well.
Examples 14-16 involved closed systems, and in all of them the total entropy either increased or stayed the same. It never decreased. Here are two examples of schemes for decreasing the entropy of a closed system, with explanations of why they don't work.
Example 17: Using a refrigerator to decrease entropy?
`=>` A refrigerator takes heat from a cold area and dumps it into a hot area. (1) Does this lead to a net decrease in the entropy of a closed system? (2) Could you make a Carnot engine more efficient by running a refrigerator to cool its low-temperature reservoir and eject heat into its high-temperature reservoir?
`=>` (1) No. The heat that comes off of the radiator coils on the back of your kitchen fridge is a great deal more than the heat the fridge removes from inside; the difference is what it costs to run your fridge. The heat radiated from the coils is so much more than the heat removed from the inside that the increase in the entropy of the air in the room is greater than the decrease of the entropy inside the fridge. The most efficient refrigerator is actually a Carnot engine running in reverse, which leads to neither an increase nor a decrease in entropy.
(2) No. The most efficient refrigerator is a reversed Carnot engine. You will not achieve anything by running one Carnot engine in reverse and another forward. They will just cancel each other out.
Hypothesis such as these lead to the following hypothesis, known as the second law of thermodynamics:

Example 18: Maxwell's daemon
`=>` Physicist James Clerk Maxwell imagined pair of neighboring rooms, their air being initially in thermal equilibrium, having a partition across the middle with a tiny door. A miniscule daemon is posted at the door with a little ping-pong paddle, and his duty is to try to build up faster-moving air molecules in room B and slower ones in room A. For instance, when a fast molecule is headed through the door, going from A to B, he lets it by, but when a slower than average molecule tries the same thing, he hits it back into room A. Would this decrease the total entropy of the pair of rooms?
`=>` No. The daemon needs to eat, and we can think of his body as a little heat engine. His metabolism is less efficient than a Carnot engine, so he ends up increasing the entropy rather than decreasing it.
Observation such as these lead to the following hypothesis, known as the second law of thermodynamics:
The entropy of a closed system always increases, or at best stays the same: `DeltaSge0`.
At present my arguments to support this statement may seem less than convincing, since they have so much to do with obscure facts about heat engines. A more satisfying and fundamental explanation for the continual increase in entropy was achieved by Ludwig Boltzmann, and you may wish to learn more about Boltzmann's ideas from my book Simple Nature, which you can download for free. Briefly, Boltzmann realized that entropy was a measure of randomness or disorder at the atomic level, and disorder doesn't spontaneously change into order.
To emphasize the fundamental and universal nature of the second law, here are a few examples.
Example 19: Entropy and evolution
A favorite argument of many creationists who don't believe in evolution is that evolution would violate the second law of thermodynamics: the death and decay of a living thing releases heat (as when a compost heap gets hot) and lessens the amount of energy available for doing useful work, while the reverse process, the emergence of life from nonliving matter, would require a decrease in entropy. Their argument is faulty, since the second law only applies to closed systems, and the earth is not a closed system. The earth is continuously receiving energy from the sun.
Example 20: The heat death of the universe
Victorian philosophers realized that living things had low entropy, as discussed in example 19, and spent a lot of time worrying about the heat death of the universe: eventually the universe would have to become a high-entropy, lukewarm soup, with no life or organized motion of any kind. Fortunately (?), we now know a great many other things that will make the universe inhospitable to life long before its entropy is maximized. Life on earth, for instance, will end when the sun evolves into a giant star and vaporizes our planet.
Example 21: Hawking radiation
Any process that could destroy heat (or convert it into nothing but mechanical work) would lead to a reduction in entropy. Black holes are supermassive stars whose gravity is so strong that nothing, not even light, can escape from them once it gets within a boundary known as the event horizon. Black holes are commonly observed to suck hot gas into them. Does this lead to a reduction in the entropy of the universe? Of course one could argue that the entropy is still there inside the black hole, but being able to “hide” entropy there amounts to the same thing as being able to destroy entropy.
The physicist Steven Hawking was bothered by this question, and finally realized that although the actual stuff that enters a black hole is lost forever, the black hole will gradually lose energy in the form of light emitted from just outside the event horizon. This light ends up reintroducing the original entropy back into the universe at large.
Homework Problems
Key
`sqrt` A computerized check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. (a) Show that under conditions of standard pressure and temperature, the volume of a sample of an ideal gas depends only on the number of molecules in it.
(b) One mole is defined as `6.0×10^(23)` atoms. Find the volume of one mole of an ideal gas, in units of liters, at standard temperature and pressure (`0°C` and 101 kPa). `sqrt`
2. A gas in a cylinder expands its volume by an amount `DeltaV`, pushing out a piston. Show that the work done by the gas on the piston is given by `DeltaW=PDeltaV`.
3. (a) A helium atom contains 2 protons, 2 electrons, and 2 neutrons. Find the mass of a helium atom. `sqrt`
(b) Find the number of atoms in 1 kg of helium. `sqrt`
(c) Helium gas is monoatomic. Find the amount of heat needed to raise the temperature of 1 kg of helium by 1 degree C. (This is known as helium's heat capacity at constant volume.) `sqrt`
4. Refrigerators, air conditioners, and heat pumps are heat engines that work in reverse. You put in mechanical work, and it the effect is to take heat out of a cooler reservoir and deposit heat in a warmer one: `Q_L+W=Q_H`. As with the heat engines discussed previously, the efficiency is defined as the energy transfer you want (`Q_L` for a refrigerator or air conditioner, `Q_H` for a heat pump) divided by the energy transfer you pay for (`W`).
Efficiencies are supposed to be unitless, but the efficiency of an air conditioner is normally given in terms of an EER rating (or a more complex version called an SEER). The EER is defined as `Q_L"/"W`, but expressed in the barbaric units of of Btu/watt-hour. A typical EER rating for a residential air conditioner is about 10 Btu/watt-hour, corresponding to an efficiency of about 3. The standard temperatures used for testing an air conditioner's efficiency are `80°F` (`27°C`) inside and `95°F` (`35°C`) outside.
(a) What would be the EER rating of a reversed Carnot engine used as an air conditioner? `sqrt`
(b) If you ran a 3-kW residential air conditioner, with an efficiency of 3, for one hour, what would be the effect on the total entropy of the universe? Is your answer consistent with the second law of thermodynamics? `sqrt`
5. (a) Estimate the pressure at the center of the Earth, assuming it is of constant density throughout. Use the technique of example 5 on page 426. Note that `g` is not constant with respect to depth --- it equals `Gmr"/"b^3` for `r`, the distance from the center, less than `b`, the earth's radius. State your result in terms of `G`, `m`, and `b`.
(b) Show that your answer from part a has the right units for pressure.
(c) Evaluate the result numerically. `sqrt`
(d) Given that the earth's atmosphere is on the order of one thousandth the thickness of the earth's radius, and that the density of the earth is several thousand times greater than the density of the lower atmosphere, check that your result is of a reasonable order of magnitude. `int`
6. (a) Determine the ratio between the escape velocities from the surfaces of the earth and the moon. `sqrt`
(b) The temperature during the lunar daytime gets up to about `130°C`. In the extremely thin (almost nonexistent) lunar atmosphere, estimate how the typical velocity of a molecule would compare with that of the same type of molecule in the earth's atmosphere. Assume that the earth's atmosphere has a temperature of `0°C`. `sqrt`
(c) Suppose you were to go to the moon and release some fluorocarbon gas, with molecular formula `C_nF_(2n+2)`. Estimate what is the smallest fluorocarbon molecule (lowest `n`) whose typical velocity would be lower than that of an `N_2` molecule on earth in proportion to the moon's lower escape velocity. The moon would be able to retain an atmosphere made of these molecules. `sqrt`
7. Most of the atoms in the universe are in the form of gas that is not part of any star or galaxy: the intergalactic medium (IGM). The IGM consists of about `10^(?5)` atoms per cubic centimeter, with a typical temperature of about `10^3` K. These are, in some sense, the density and temperature of the universe (not counting light, or the exotic particles known as “dark matter”). Calculate the pressure of the universe (or, speaking more carefully, the typical pressure due to the IGM). `sqrt`
8. A sample of gas is enclosed in a sealed chamber. The gas consists of molecules, which are then split in half through some process such as exposure to ultraviolet light, or passing an electric spark through the gas. The gas returns to thermal equilibrium with the surrounding room. How does its pressure now compare with its pressure before the molecules were split?

9. The figure shows a demonstration performed by Otto von Guericke for Emperor Ferdinand III, in which two teams of horses failed to pull apart a pair of hemispheres from which the air had been evacuated. (a) What object makes the force that holds the hemispheres together? (b) The hemispheres are in a museum in Berlin, and have a diameter of 65 cm. What is the amount of force holding them together? (Hint: The answer would be the same if they were cylinders or pie plates rather then hemispheres.)
16.2 Microscopic description of an ideal gas by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.