16.1 Pressure and temperature by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
16.1 Pressure and temperature
When we heat an object, we speed up the mind-bogglingly complex random motion of its molecules. One method for taming complexity is the conservation laws, since they tell us that certain things must remain constant regardless of what process is going on. Indeed, the law of conservation of energy is also known as the first law of thermodynamics.
But as alluded to in the introduction to this chapter, conservation of energy by itself is not powerful enough to explain certain empirical facts about heat. A second way to sidestep the complexity of heat is to ignore heat's atomic nature and concentrate on quantities like temperature and pressure that tell us about a system's properties as a whole. This approach is called macroscopic in contrast to the microscopic method of attack. Pressure and temperature were fairly well understood in the age of Newton and Galileo, hundreds of years before there was any firm evidence that atoms and molecules even existed.
Unlike the conserved quantities such as mass, energy, momentum, and angular momentum, neither pressure nor temperature is additive. Two cups of coffee have twice the heat energy of a single cup, but they do not have twice the temperature. Likewise, the painful pressure on your eardrums at the bottom of a pool is not affected if you insert or remove a partition between the two halves of the pool.
Pressure
 If you're at the bottom of a pool, you can't relieve the pain in your ears by turning your head. The water's force on your eardrum is always the same, and is always perpendicular to the surface where the eardrum contacts the water. If your ear is on the east side of your head, the water's force is to the west. If you keep your head in the same spot while turning around so your ear is on the north, the force will still be the same in magnitude, and it will change its direction so that it is still perpendicular to the eardrum: south. This shows that pressure has no direction in space, i.e., it is a scalar. The direction of the force is determined by the orientation of the surface on which the pressure acts, not by the pressure itself. A fluid flowing over a surface can also exert frictional forces, which are parallel to the surface, but the present discussion is restricted to fluids at rest.
If you're at the bottom of a pool, you can't relieve the pain in your ears by turning your head. The water's force on your eardrum is always the same, and is always perpendicular to the surface where the eardrum contacts the water. If your ear is on the east side of your head, the water's force is to the west. If you keep your head in the same spot while turning around so your ear is on the north, the force will still be the same in magnitude, and it will change its direction so that it is still perpendicular to the eardrum: south. This shows that pressure has no direction in space, i.e., it is a scalar. The direction of the force is determined by the orientation of the surface on which the pressure acts, not by the pressure itself. A fluid flowing over a surface can also exert frictional forces, which are parallel to the surface, but the present discussion is restricted to fluids at rest.
Experiments also show that a fluid's force on a surface is proportional to the surface area. The vast force of the water behind a dam, for example, in proportion to the dam's great surface area. (The bottom of the dam experiences a higher proportion of its force.)
Based on these experimental results, it appears that the useful way to define pressure is as follows. The pressure of a fluid at a given point is defined as `F_(bot)"/"A`, where `A` is the area of a small surface inserted in the fluid at that point, and `F_(bot)` is the component of the fluid's force on the surface which is perpendicular to the surface.
This is essentially how a pressure gauge works. The reason that the surface must be small is so that there will not be any significant difference in pressure between one part of it and another part. The SI units of pressure are evidently `N"/"m^2`, and this combination can be abbreviated as the pascal, `1 Pa=1 N"/"m^2`. The pascal turns out to be an inconveniently small unit, so car tires, for example, have recommended pressures imprinted on them in units of kilopascals.
Example 1: Pressure in U.S. units
In U.S. units, the unit of force is the pound, and the unit of distance is the inch. The unit of pressure is therefore pounds per square inch, or p.s.i. (Note that the pound is not a unit of mass.)
Example 2: Atmospheric pressure in U.S. and metric units
`=>` A figure that many people in the U.S. remember is that atmospheric pressure is about 15 pounds per square inch. What is this in metric units?
`=>` `(15 lb)/(1 "in"^2)=(68 N)/(0.0254 m)^2`
`=1.0×10^5 N"/"m^2`
`=100 kPa`
Only pressure differences are normally significant.
Example 3: Getting killed by a pool pump
`=>` My house has a pool, which I maintain myself. A pool always needs to have its water circulated through a filter for several hours a day in order to keep it clean. The filter is a large barrel with a strong clamp that holds the top and bottom halves together. My filter has a prominent warning label that warns me not to try to open the clamps while the pump is on, and it shows a cartoon of a person being struck by the top half of the pump. The cross-sectional area of the filter barrel is `0.25 m^2`. Like most pressure gauges, the one on my pool pump actually reads the difference in pressure between the pressure inside the pump and atmospheric pressure. The gauge reads 90 kPa. What is the force that is trying to pop open the filter?
`=>` If the gauge told us the absolute pressure of the water inside, we'd have to find the force of the water pushing outward and the force of the air pushing inward, and subtract in order to find the total force. Since air surrounds us all the time, we would have to do such a subtraction every time we wanted to calculate anything useful based on the gauge's reading. The manufacturers of the gauge decided to save us from all this work by making it read the difference in pressure between inside and outside, so all we have to do is multiply the gauge reading by the cross-sectional area of the filter:
[Private Equation]
`=(90×10^3 N"/"m^2)(0.25 m^2) =22000 N`
 That's a lot of force!
That's a lot of force!
The word “suction” and other related words contain a hidden misunderstanding related to this point about pressure differences. When you suck water up through a straw, there is nothing in your mouth that is attracting the water upward. The force that lifts the water is from the pressure of the water in the cup. By creating a partial vacuum in your mouth, you decreased the air's downward force on the water so that it no longer exactly canceled the upward force.
Variation of pressure with depth
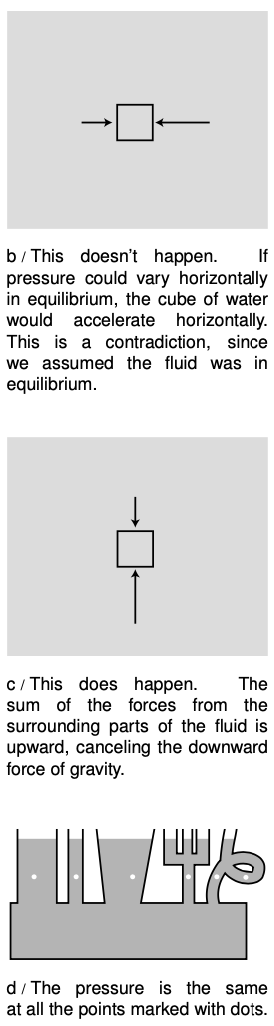
The pressure within a fluid in equilibrium can only depend on depth, due to gravity. If the pressure could vary from side to side, then a piece of the fluid in between, b, would be subject to unequal forces from the parts of the fluid on its two sides. But fluids do not exhibit shear forces, so there would be no other force that could keep this piece of fluid from accelerating. This contradicts the assumption that the fluid was in equilibrium.
self-check:
How does this proof fail for solids?
(answer in the back of the PDF version of the book)
To find the variation with depth, we consider the vertical forces acting on a tiny, imaginary cube of the fluid having height `Deltay` and areas `dA` on the top and bottom. Using positive numbers for upward forces, we have
`P_"bottom"DeltaA-P_"top"DeltaA-F_g=0.`
The weight of the fluid is `F_g=mg=rhoVg=rhoDeltaADeltayg`, where `rho` is the density of the fluid, so the difference in pressure is
`Delta P = -rhogDeltay` . [variation in pressure with depth for a fluid of density `rho` in equilibrium; positive `y` is up.]
The factor of `rho` explains why we notice the difference in pressure when diving 3 m down in a pool, but not when going down 3 m of stairs. Note also that the equation only tells us the difference in pressure, not the absolute pressure. The pressure at the surface of a swimming pool equals the atmospheric pressure, not zero, even though the depth is zero at the surface. The blood in your body does not even have an upper surface.
Example 4: Pressure of lava underneath a volcano
`=>` A volcano has just finished erupting, and a pool of molten lava is lying at rest in the crater. The lava has come up through an opening inside the volcano that connects to the earth's molten mantle. The density of the lava is `4.1 g"/"cm^3`. What is the pressure in the lava underneath the base of the volcano, 3000 m below the surface of the pool?
`=>` `DeltaP=rhogDeltay`
`=(4.1 g"/"cm^3)(9.8 m"/"s^2)(3000 m)`
`=(4.1×10^6 g"/"m^3)(9.8 m"/"s^2)(3000 m)`
`=(4.1×10^3 kg"/"m^3)(9.8 m"/"s^2)(3000 m)`
`=1.2×10^8 N"/"m^2=1.2×10^8 Pa`
`=1.2×10^8 Pa`
This is the difference between the pressure we want to find and atmospheric pressure at the surface. The latter, however, is tiny compared to the `DeltaP` we just calculated, so what we've found is essentially the pressure, `P`.
Example 5: Atmospheric pressure
This example uses calculus.
Gases, unlike liquids, are quite compressible, and at a given temperature, the density of a gas is approximately proportional to the pressure. The proportionality constant is discussed in section 16.2, but for now let's just call it `k`, `rho=kP`. Using this fact, we can find the variation of atmospheric pressure with altitude, assuming constant temperature:
`dP=-rhogdy`
`dP=-kPgdy`
`(dP)/P=-kgdy`
`lnP=-kgy+"constant"["integrating both sides"]`
`P=("constant")e^(-kgy)["exponentiating both sides"]`
Pressure falls off exponentially with height. There is no sharp cutoff to the atmosphere, but the exponential gets extremely small by the time you're ten or a hundred miles up.
 Temperature
Temperature
Thermal equilibrium
We use the term temperature casually, but what is it exactly? Roughly speaking, temperature is a measure of how concentrated the heat energy is in an object. A large, massive object with very little heat energy in it has a low temperature.
But physics deals with operational definitions, i.e., definitions of how to measure the thing in question. How do we measure temperature? One common feature of all temperature-measuring devices is that they must be left for a while in contact with the thing whose temperature is being measured. When you take your temperature with a fever thermometer, you wait for the mercury inside to come up to the same temperature as your body. The thermometer actually tells you the temperature of its own working fluid (in this case the mercury). In general, the idea of temperature depends on the concept of thermal equilibrium. When you mix cold eggs from the refrigerator with flour that has been at room temperature, they rapidly reach a compromise temperature. What determines this compromise temperature is conservation of energy, and the amount of energy required to heat or cool each substance by one degree. But without even having constructed a temperature scale, we can see that the important point is the phenomenon of thermal equilibrium itself: two objects left in contact will approach the same temperature. We also assume that if object A is at the same temperature as object B, and B is at the same temperature as C, then A is at the same temperature as C. This statement is sometimes known as the zeroth law of thermodynamics, so called because after the first, second, and third laws had been developed, it was realized that there was another law that was even more fundamental.
 Thermal expansion
Thermal expansion
The familiar mercury thermometer operates on the principle that the mercury, its working fluid, expands when heated and contracts when cooled. In general, all substances expand and contract with changes in temperature. The zeroth law of thermodynamics guarantees that we can construct a comparative scale of temperatures that is independent of what type of thermometer we use. If a thermometer gives a certain reading when it's in thermal equilibrium with object A, and also gives the same reading for object B, then A and B must be the same temperature, regardless of the details of how the thermometers works.
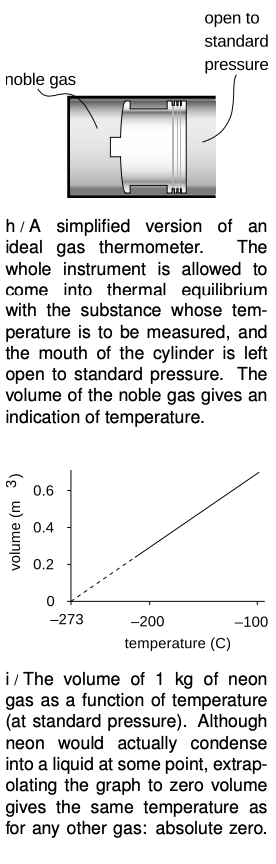
What about constructing a temperature scale in which every degree represents an equal step in temperature? The Celsius scale has 0 as the freezing point of water and 100 as its boiling point. The hidden assumption behind all this is that since two points define a line, any two thermometers that agree at two points must agree at all other points. In reality if we calibrate a mercury thermometer and an alcohol thermometer in this way, we will find that a graph of one thermometer's reading versus the other is not a perfectly straight `y=x` line. The subtle inconsistency becomes a drastic one when we try to extend the temperature scale through the points where mercury and alcohol boil or freeze. Gases, however, are much more consistent among themselves in their thermal expansion than solids or liquids, and the noble gases like helium and neon are more consistent with each other than gases in general. Continuing to search for consistency, we find that noble gases are more consistent with each other when their pressure is very low.
As an idealization, we imagine a gas in which the atoms interact only with the sides of the container, not with each other. Such a gas is perfectly nonreactive (as the noble gases very nearly are), and never condenses to a liquid (as the noble gases do only at extremely low temperatures). Its atoms take up a negligible fraction of the available volume. Any gas can be made to behave very much like this if the pressure is extremely low, so that the atoms hardly ever encounter each other. Such a gas is called an ideal gas, and we define the Celsius scale in terms of the volume of the gas in a thermometer whose working substance is an ideal gas maintained at a fixed (very low) pressure, and which is calibrated at 0 and 100 degrees according to the melting and boiling points of water. The Celsius scale is not just a comparative scale but an additive one as well: every step in temperature is equal, and it makes sense to say that the difference in temperature between 18 and 28°C is the same as the difference between 48 and 58.
 Absolute zero and the kelvin scale
Absolute zero and the kelvin scale
We find that if we extrapolate a graph of volume versus temperature, the volume becomes zero at nearly the same temperature for all gases: -273°C. Real gases will all condense into liquids at some temperature above this, but an ideal gas would achieve zero volume at this temperature, known as absolute zero. The most useful temperature scale in scientific work is one whose zero is defined by absolute zero, rather than by some arbitrary standard like the melting point of water. The ideal temperature scale for scientific work, called the Kelvin scale, is the same as the Celsius scale, but shifted by 273 degrees to make its zero coincide with absolute zero. Scientists use the Celsius scale only for comparisons or when a change in temperature is all that is required for a calculation. Only on the Kelvin scale does it make sense to discuss ratios of temperatures, e.g., to say that one temperature is twice as hot as another.
Example 6: Which temperature scale to use
`=>` You open an astronomy book and encounter the equation
`("light emitted")=("constant")×T^4`
for the light emitted by a star as a function of its surface temperature. What temperature scale is implied?
`=>` The equation tells us that doubling the temperature results in the emission of 16 times as much light. Such a ratio only makes sense if the Kelvin scale is used.
16.1 Pressure and temperature by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.