15.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
angular momentum — a measure of rotational motion; a conserved quantity for a closed system
axis — An arbitrarily chosen point used in the definition of angular momentum. Any object whose direction changes relative to the axis is considered to have angular momentum. No matter what axis is chosen, the angular momentum of a closed system is conserved.
torque — the rate of change of angular momentum; a numerical measure of a force's ability to twist on an object
equilibrium — a state in which an object's momentum and angular momentum are constant
stable equilibrium — one in which a force always acts to bring the object back to a certain point
unstable equilibrium — one in which any deviation of the object from its equilibrium position results in a force pushing it even farther away
Notation
`L` — angular momentum
`t` — torque
`T` — the time required for a rigidly rotating body to complete one rotation
Other Notation
period — a name for the variable `T` defined above
moment of inertia, `I` — the proportionality constant in the equation `L=2piI"/"T`
Summary
Angular momentum is a measure of rotational motion which is conserved for a closed system. This book only discusses angular momentum for rotation of material objects in two dimensions. Not all rotation is rigid like that of a wheel or a spinning top. An example of nonrigid rotation is a cyclone, in which the inner parts take less time to complete a revolution than the outer parts. In order to define a measure of rotational motion general enough to include nonrigid rotation, we define the angular momentum of a system by dividing it up into small parts, and adding up all the angular momenta of the small parts, which we think of as tiny particles. We arbitrarily choose some point in space, the axis, and we say that anything that changes its direction relative to that point possesses angular momentum. The angular momentum of a single particle is
where `v_(bot)` is the component of its velocity perpendicular to the line joining it to the axis, and `r` is its distance from the axis. Positive and negative signs of angular momentum are used to indicate clockwise and counterclockwise rotation.
The choice of axis theorem states that any axis may be used for defining angular momentum. If a system's angular momentum is constant for one choice of axis, then it is also constant for any other choice of axis.
The spin theorem states that an object's angular momentum with respect to some outside axis `A` can be found by adding up two parts:
(1) The first part is the object's angular momentum found by using its own center of mass as the axis, i.e., the angular momentum the object has because it is spinning.
(2) The other part equals the angular momentum that the object would have with respect to the axis `A` if it had all its mass concentrated at and moving with its center of mass.
Torque is the rate of change of angular momentum. The torque a force can produce is a measure of its ability to twist on an object. The relationship between force and torque is
`|tau|=r|F_(bot)|`,
where `r` is the distance from the axis to the point where the force is applied, and `F_(bot)`is the component of the force perpendicular to the line connecting the axis to the point of application. Statics problems can be solved by setting the total force and total torque on an object equal to zero and solving for the unknowns.
Homework Problems
Key
`sqrt` - A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. You are trying to loosen a stuck bolt on your `RV` using a big wrench that is 50 cm long. If you hang from the wrench, and your mass is 55 kg, what is the maximum torque you can exert on the bolt? `sqrt`
2. A physical therapist wants her patient to rehabilitate his injured elbow by laying his arm flat on a table, and then lifting a 2.1 kg mass by bending his elbow. In this situation, the weight is 33 cm from his elbow. He calls her back, complaining that it hurts him to grasp the weight. He asks if he can strap a bigger weight onto his arm, only 17 cm from his elbow. How much mass should she tell him to use so that he will be exerting the same torque? (He is raising his forearm itself, as well as the weight.) `sqrt`
3. An object thrown straight up in the air is momentarily at rest when it reaches the top of its motion. Does that mean that it is in equilibrium at that point? Explain.
4. An object is observed to have constant angular momentum. Can you conclude that no torques are acting on it? 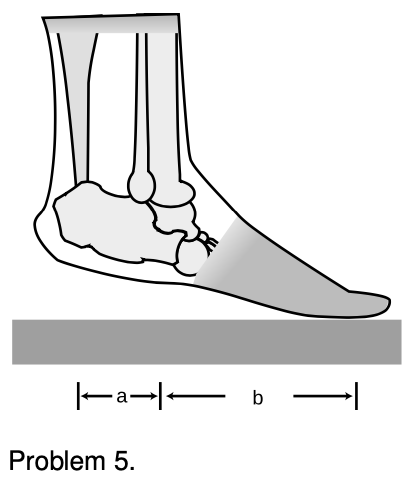 Explain. [Based on a problem by Serway and Faughn.]
Explain. [Based on a problem by Serway and Faughn.]
5. A person of weight `W` stands on the ball of one foot. Find the tension in the calf muscle and the force exerted by the shinbones on the bones of the foot, in terms of `W`, `a`, and `b`. For simplicity, assume that all the forces are at 90-degree angles to the foot, i.e., neglect the angle between the foot and the floor. `sqrt`
6. Two objects have the same momentum vector. Assume that they are not spinning; they only have angular momentum due to their motion through space. Can you conclude that their angular momenta are the same? Explain. [Based on a problem by Serway and Faughn.]
7. The sun turns on its axis once every 26.0 days. Its mass is `2.0×10^30 kg` and its radius is `7.0×10^8 m`. Assume it is a rigid sphere of uniform density.
 (a) What is the sun's angular momentum? `sqrt`
(a) What is the sun's angular momentum? `sqrt`
In a few billion years, astrophysicists predict that the sun will use up all its sources of nuclear energy, and will collapse into a ball of exotic, dense matter known as a white dwarf. Assume that its radius becomes `5.8×10^6 m` (similar to the size of the Earth.) Assume it does not lose any mass between now and then. (Don't be fooled by the photo, which makes it look like nearly all of the star was thrown off by the explosion. The visually prominent gas cloud is actually thinner than the best laboratory vacuum ever produced on earth. Certainly a little bit of mass is actually lost, but it is not at all unreasonable to make an approximation of zero loss of mass as we are doing.)
(b) What will its angular momentum be?
(c) How long will it take to turn once on its axis? `sqrt`
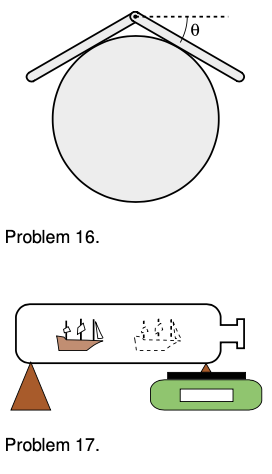
8. A uniform ladder of mass mm and length `L` leans against a smooth wall, making an angle `theta` with respect to the ground. The dirt exerts a normal force and a frictional force on the ladder, producing a force vector with magnitude `F_1` at an angle `phi` with respect to the ground. Since the wall is smooth, it exerts only a normal force on the ladder; let its magnitude be `F_2`.
(a) Explain why `phi` must be greater than `phi`. No math is needed.
(b) Choose any numerical values you like for `m` and `L`, and show that the ladder can be in equilibrium (zero torque and zero total force vector) for `theta=45.00°` and `var=63.43°`.
9. Continuing the previous problem, find an equation for `phi` in terms of `theta`, and show that `m` and `L` do not enter into the equation. Do not assume any numerical values for any of the variables. You will need the trig identity `sin(a-b)=sinacosb-sinbcosa`. (As a numerical check on your result, you may wish to check that the angles given in part `b` of the previous problem satisfy your equation.) `sqrt` `***`
10. (a) Find the minimum horizontal force which, applied at the axle, will pull a wheel over a step. Invent algebra symbols for whatever quantities you find to be relevant, and give your answer in symbolic form. [Hints: There are four forces on the wheel at first, but only three when it lifts off. Normal forces are always perpendicular to the surface of contact. Note that the corner of the step cannot be perfectly sharp, so the surface of contact for this force really coincides with the surface of the wheel.]
(b) Under what circumstances does your result become infinite? Give a physical interpretation.
11. A yo-yo of total mass mm consists of two solid cylinders of radius `R`, connected by a small spindle of negligible mass and radius `r`. The top of the string is held motionless while the string unrolls from the spindle. Show that the acceleration of the yo-yo is `g"/"(1+R^2"/"2r^2)`. [Hint: The acceleration and the tension in the string are unknown. Use `tau=DeltaL"/"Deltat` and `F=ma` to determine these two unknowns.] `***`
12. A ball is connected by a string to a vertical post. The ball is set in horizontal motion so that it starts winding the string around the post. Assume that the motion is confined to a horizontal plane, i.e., ignore gravity. Michelle and Astrid are trying to predict the final velocity of the ball when it reaches the post. Michelle says that according to conservation of angular momentum, the ball has to speed up as it approaches the post. Astrid says that according to conservation of energy, the ball has to keep a constant speed. Who is right? [Hint: How is this different from the case where you whirl a rock in a circle on a string and gradually reel in the string?]
13. In the 1950's, serious articles began appearing in magazines like Life predicting that world domination would be achieved by the nation that could put nuclear bombs in orbiting space stations, from which they could be dropped at will. In fact it can be quite difficult to get an orbiting object to come down. Let the object have energy `E=KE + PE` and angular momentum `L`. Assume that the energy is negative, i.e., the object is moving at less than escape velocity. Show that it can never reach a radius less than
`r_min=(GMm)/(2E)(-1+sqrt(1+(2EL^2)/(G^2M^2m^3)))`.
[Note that both factors are negative, giving a positive result.]
15. [Problem 15 has been deleted.] `***`
 16. Two bars of length `L` are connected with a hinge and placed on a frictionless cylinder of radius `r`. (a) Show that the angle `theta` shown in the figure is related to the unitless ratio `r"/"L` by the equation
16. Two bars of length `L` are connected with a hinge and placed on a frictionless cylinder of radius `r`. (a) Show that the angle `theta` shown in the figure is related to the unitless ratio `r"/"L` by the equation
`r/L=(cos^2theta)/(2tantheta).`
(b) Discuss the physical behavior of this equation for very large and very small values of `r"/"L`. `***`
17. You wish to determine the mass of a ship in a bottle without taking it out. Show that this can be done with the setup shown in the figure, with a scale supporting the bottle at one end, provided that it is possible to take readings with the ship slid to several different locations. Note that you can't determine the position of the ship's center of mass just by looking at it, and likewise for the bottle. In particular, you can't just say, “position the ship right on top of the fulcrum” or “position it right on top of the balance.”
18. Two atoms will interact via electrical forces between their protons and electrons. One fairly good approximation to the potential energy is the Lennard-Jones formula,
`PE(r)=k[(a/r)^(12)-2(a/r)^6]`,
where `r` is the center-to-center distance between the atoms and `k` is a positive constant. Show that (a) there is an equilibrium point at `r=a`,
(b) the equilibrium is stable, and
(c) the energy required to bring the atoms from their equilibrium separation to infinity is `k`. `int`
19. Suppose that we lived in a universe in which Newton's law of gravity gave forces proportional to `r^(-7)` rather than `r^(-2)`. Which, if any, of Kepler's laws would still be true? Which would be completely false? Which would be different, but in a way that could be calculated with straightforward algebra?
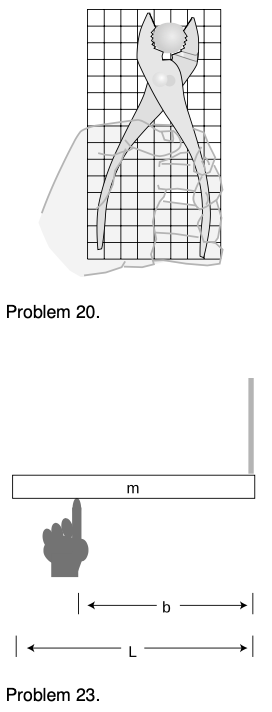 20. The figure shows scale drawing of a pair of pliers being used to crack a nut, with an appropriately reduced centimeter grid. Warning: do not attempt this at home; it is bad manners. If the force required to crack the nut is 300 N, estimate the force required of the person's hand.
20. The figure shows scale drawing of a pair of pliers being used to crack a nut, with an appropriately reduced centimeter grid. Warning: do not attempt this at home; it is bad manners. If the force required to crack the nut is 300 N, estimate the force required of the person's hand.
21. Show that a sphere of radius `R` that is rolling without slipping has angular momentum and momentum in the ratio `L"/"p=(2"/"5)R`.
22. Suppose a bowling ball is initially thrown so that it has no angular momentum at all, i.e., it is initially just sliding down the lane. Eventually kinetic friction will get it spinning fast enough so that it is rolling without slipping. Show that the final velocity of the ball equals 5/7 of its initial velocity. [Hint: You'll need the result of problem 21.]
23. The rod in the figure is supported by the finger and the string.
(a) Find the tension, `T`, in the string, and the force, `F`, from the finger, in terms of `m,b,L` and `g`. `sqrt`
(b) Comment on the cases `b=L` and `b=L/2`.
(c) Are any values of `b` unphysical?
24. Two horizontal tree branches on the same tree have equal diameters, but one branch is twice as long as the other. Give a quantitative comparison of the torques where the branches join the trunk. [Thanks to Bong Kang.]
25. (a) Alice says Cathy's body has zero momentum, but Bob says Cathy's momentum is nonzero. Nobody is lying or making a mistake. How is this possible? Give a concrete example.
(b) Alice and Bob agree that Dong's body has nonzero momentum, but disagree about Dong's angular momentum, which Alice says is zero, and Bob says is nonzero. Explain.
26. Penguins are playful animals. Tux the Penguin invents a new game using a natural circular depression in the ice. He waddles at top speed toward the crater, aiming off to the side, and then hops into the air and lands on his belly just inside its lip. He then belly-surfs, moving in a circle around the rim. The ice is frictionless, so his speed is constant. Is Tux's angular momentum zero, or nonzero? What about the total torque acting on him? Take the center of the crater to be the axis. Explain your answers.
 27. Make a rough estimate of the mechanical advantage of the lever shown in the figure. In other words, for a given amount of force applied on the handle, how many times greater is the resulting force on the cork?
27. Make a rough estimate of the mechanical advantage of the lever shown in the figure. In other words, for a given amount of force applied on the handle, how many times greater is the resulting force on the cork?
28. In example 8 on page 397, prove that if the rod is sufficiently thin, it can be toppled without scraping on the floor. `***`
29. A massless rod of length `?` has weights, each of mass `m`, attached to its ends. The rod is initially put in a horizontal position, and laid on an off-center fulcrum located at a distance `b` from the rod's center. The rod will topple. (a) Calculate the total gravitational torque on the rod directly, by adding the two torques. (b) Verify that this gives the same result as would have been obtained by taking the entire gravitational force as acting at the center of mass.
30. A skilled motorcyclist can ride up a ramp, fly through the air, and land on another ramp. Why would it be useful for the rider to speed up or slow down the back wheel while in the air?
Exercise 15: Torque
Equipment:
- rulers with holes in them
- spring scales (two per group)
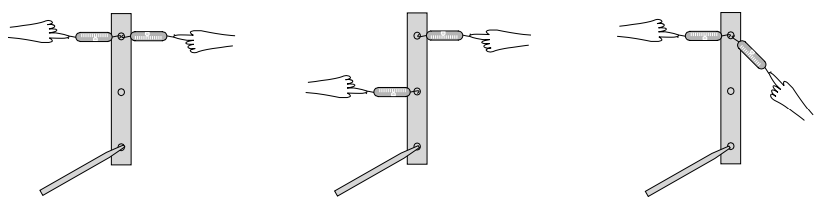
While one person holds the pencil which forms the axle for the ruler, the other members of the group pull on the scale and take readings. In each case, calculate the total torque on the ruler, and find out whether it equals zero to roughly within the accuracy of the experiment. Finish the calculations for each part before moving on to the next one .
15.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.