15.5 Statics by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
15.5 Statics
Equilibrium
There are many cases where a system is not closed but maintains constant angular momentum. When a merry-go-round is running at constant angular momentum, the engine's torque is being canceled by the torque due to friction.
When an object has constant momentum and constant angular momentum, we say that it is in equilibrium. This is a scientific redefinition of the common English word, since in ordinary speech nobody would describe a car spinning out on an icy road as being in equilibrium.
Very commonly, however, we are interested in cases where an object is not only in equilibrium but also at rest, and this corresponds more closely to the usual meaning of the word. Trees and bridges have been designed by evolution and engineers to stay at rest, and to do so they must have not just zero total force acting on them but zero total torque. It is  not enough that they don't fall down, they also must not tip over. Statics is the branch of physics concerned with problems such as these.
not enough that they don't fall down, they also must not tip over. Statics is the branch of physics concerned with problems such as these.
Solving statics problems is now simply a matter of applying and combining some things you already know:
- You know the behaviors of the various types of forces, for example that a frictional force is always parallel to the surface of contact.
- You know about vector addition of forces. It is the vector sum of the forces that must equal zero to produce equilibrium.
- You know about torque. The total torque acting on an object must be zero if it is to be in equilibrium.
- You know that the choice of axis is arbitrary, so you can make a choice of axis that makes the problem easy to solve.
In general, this type of problem could involve four equations in four unknowns: three equations that say the force components add up to zero, and one equation that says the total torque is zero. Most cases you'll encounter will not be this complicated. In the following example, only the equation for zero total torque is required in order to get an answer.
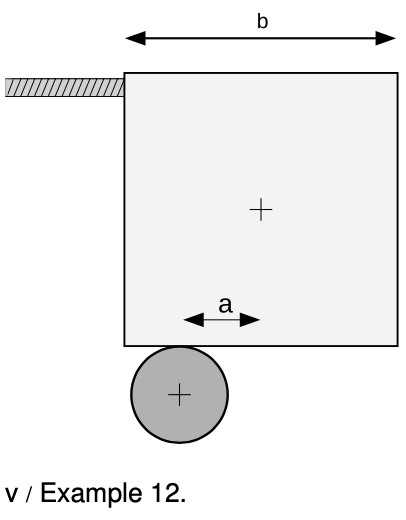 Example 12: Art!
Example 12: Art!
`=>` The abstract sculpture shown in figure v contains a cube of mass mm and sides of length `b`. The cube rests on top of a cylinder, which is off-center by a distance `a`. Find the tension in the cable.
`=>` There are four forces on the cube: a gravitational force `mg`, the force `F_T` from the cable, the upward normal force from the cylinder, `F_N`, and the horizontal static frictional force from the cylinder, `F_s`.
The total force on the cube in the vertical direction is zero:
`F_N-mg=0`.
As our axis for defining torques, it's convenient to choose the point of contact between the cube and the cylinder, because then neither `F_s` nor `F_N` makes any torque. The cable's torque is counterclockwise, the torque due to gravity is clockwise. Letting counterclockwise torques be positive, and using the convenient equation `tau=r_(bot)F`, we find the equation for the total torque:
`bF_T-mga=0.`
We could also write down the equation saying that the total horizontal force is zero, but that would bring in the cylinder's frictional force on the cube, which we don't know and don't need to find. We already have two equations in the two unknowns `F_T` and `F_N`, so there's no need to make it into three equations in three unknowns. Solving the first equation for `F_N=mg`, we then substitute into the second equation to eliminate `F_N`, and solve for `F_T=(a"/"b)mg`.
As a check, our result makes sense when `a=0`; the cube is balanced on the cylinder, so the cable goes slack.
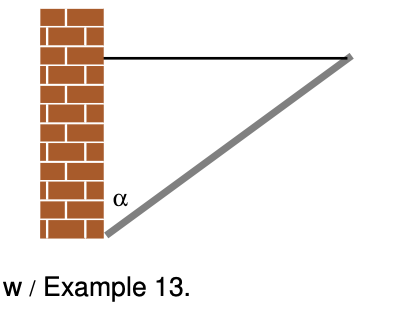 Example 13: A flagpole
Example 13: A flagpole
`=>` A 10-kg flagpole is being held up by a lightweight horizontal cable, and is propped against the foot of a wall as shown in the figure. If the cable is only capable of supporting a tension of 70 N, how great can the angle `alpha` be without breaking the cable?
`=>` All three objects in the figure are supposed to be in equilibrium: the pole, the cable, and the wall. Whichever of the three objects we pick to investigate, all the forces and torques on it have to cancel out. It is not particularly helpful to analyze the forces and torques on the wall, since it has forces on it from the ground that are not given and that we don't want to find. We could study the forces and torques on the cable, but that doesn't let us use the given information about the pole. The object we need to analyze is the pole.
The pole has three forces on it, each of which may also result in a torque: (1) the gravitational force, (2) the cable's force, and (3) the wall's force.
We are free to define an axis of rotation at any point we wish, and it is helpful to define it to lie at the bottom end of the pole, since by that definition the wall's force on the pole is applied at `r=0` and thus makes no torque on the pole. This is good, because we don't know what the wall's force on the pole is, and we are not trying to find it.
With this choice of axis, there are two nonzero torques on the pole, a counterclockwise torque from the cable and a clockwise torque from gravity. Choosing to represent counterclockwise torques as positive numbers, and using the equation `|tau|=r|F|sintheta`, we have
`r_"cable"|F_"cable"|sintheta_"cable"-r_"grav"|F_"grav"|sintheta_"grav"=0`.
A little geometry gives: `theta_"cable"=90°-alpha` and `theta_"grav"=alpha`, so
`r_"cable"|F_"cable"|sin(90°-alpha)-r_"grav"|F_"grav"|sinalpha=0`.
The gravitational force can be considered as acting at the pole's center of mass, i.e., at its geometrical center, so `r_"cable"` is twice `r_"grav"`, and we can simplify the equation to read
`2|F_"cable"|sin(90°-alpha)-|F_"grav"|sinalpha=0`.
These are all quantities we were given, except for `alpha`, which is the angle we want to find. To solve for `alpha` we need to use the trig identity `sin(90°-x)=cosx`,
`2|F_"cable"|cosalpha-|F_"grav"|sinalpha=0`,
which allows us to find
`tanalpha=2|F_"cable"|/|F_"grav"|`
`alpha=tan^(-1)(2|F_"cable"|/|F_"grav"|)`
`=tan^(-1)(2×(70 N)/(98 N))`
`=55°`.
 Stable and unstable equilibria
Stable and unstable equilibria
A pencil balanced upright on its tip could theoretically be in equilibrium, but even if it was initially perfectly balanced, it would topple in response to the first air current or vibration from a passing truck. The pencil can be put in equilibrium, but not in stable equilibrium. The things around us that we really do see staying still are all in stable equilibrium.
Why is one equilibrium stable and another unstable? Try pushing your own nose to the left or the right. If you push it a millimeter to the left, your head responds with a gentle force to the right, which keeps your nose from flying off of your face. If you push your nose a centimeter to the left, your face's force on your nose becomes much stronger. The defining characteristic of a stable equilibrium is that the farther the object is moved away from equilibrium, the stronger the force is that tries to bring it back.
The opposite is true for an unstable equilibrium. In the top figure, the ball resting on the round hill theoretically has zero total force on it when it is exactly at the top. But in reality the total force will not be exactly zero, and the ball will begin to move off to one side. Once it has moved, the net force on the ball is greater than it was, and it accelerates more rapidly. In an unstable equilibrium, the farther the object gets from equilibrium, the stronger the force that pushes it farther from equilibrium.
This idea can be rephrased in terms of energy. The difference between the stable and unstable equilibria shown in figure x is that in the stable equilibrium, the potential energy is at a minimum, and moving to either side of equilibrium will increase it, whereas the unstable equilibrium represents a maximum.
Note that we are using the term “stable” in a weaker sense than in ordinary speech. A domino standing upright is stable in the sense we are using, since it will not spontaneously fall over in response to a sneeze from across the room or the vibration from a passing truck. We would only call it unstable in the technical sense if it could be toppled by any force, no matter how small. In everyday usage, of course, it would be considered unstable, since the force required to topple it is so small.
Example 14: An application of calculus
`=>` Nancy Neutron is living in a uranium nucleus that is undergoing fission. Nancy's potential energy as a function of position can be approximated by `PE=x^4-x^2`, where all the units and numerical constants have been suppressed for simplicity. Use calculus to locate the equilibrium points, and determine whether they are stable or unstable.
`=>` The equilibrium points occur where the `PE` is at a minimum or maximum, and minima and maxima occur where the derivative (which equals minus the force on Nancy) is zero. This derivative is `dPE"/"dx=4x^3-2x`, and setting it equal to zero, we have `x=0,±1"/"sqrt(2)`. Minima occur where the second derivative is positive, and maxima where it is negative. The second derivative is `12x^2-2`, which is negative at `x=0` (unstable) and positive at `x=±1"/"sqrt(2)` (stable). Interpretation: the graph of the `PE` is shaped like a rounded letter `W,' with the two troughs representing the two halves of the splitting nucleus. Nancy is going to have to decide which half she wants to go with.
15.5 Statics by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.