15.3 Two theorems about angular momentum by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
15.3 Two theorems about angular momentum
With plain old momentum, `p`, we had the freedom to work in any inertial frame of reference we liked. The same object could have different values of momentum in two different frames, if the frames were not at rest with respect to each other. Conservation of momentum, however, would be true in either frame. As long as we employed a single frame consistently throughout a calculation, everything would work.
The same is true for angular momentum, and in addition there is an ambiguity that arises from the definition of an axis of rotation. For a wheel, the natural choice of an axis of rotation is obviously the axle, but what about an egg rotating on its side? The egg has an asymmetric shape, and thus no clearly defined geometric center. A similar issue arises for a cyclone, which does not even have a sharply defined shape, or for a complicated machine with many gears. The 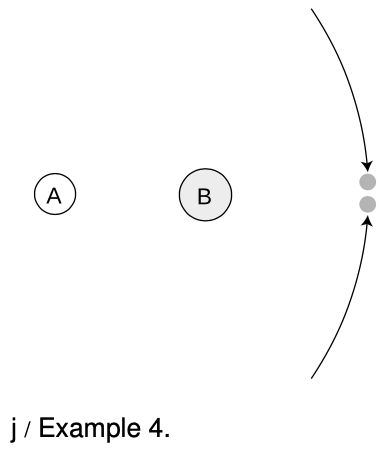 following theorem, the first of two presented in this section without proof, explains how to deal with this issue. Although I have put descriptive titles above both theorems, they have no generally accepted names.
following theorem, the first of two presented in this section without proof, explains how to deal with this issue. Although I have put descriptive titles above both theorems, they have no generally accepted names.
the choice of axis theorem
It is entirely arbitrary what point one defines as the axis for purposes of calculating angular momentum. If a closed system's angular momentum is conserved when calculated with one choice of axis, then it will also be conserved for any other choice. Likewise, any inertial frame of reference may be used.
 Example 4: Colliding asteroids described with different axes
Example 4: Colliding asteroids described with different axes
Observers on planets `A` and `B` both see the two asteroids colliding. The asteroids are of equal mass and their impact speeds are the same. Astronomers on each planet decide to define their own planet as the axis of rotation. Planet `A` is twice as far from the collision as planet `B`. The asteroids collide and stick. For simplicity, assume planets `A` and `B` are both at rest.
With planet `A` as the axis, the two asteroids have the same amount of angular momentum, but one has positive angular momentum and the other has negative. Before the collision, the total angular momentum is therefore zero. After the collision, the two asteroids will have stopped moving, and again the total angular momentum is zero. The total angular momentum both before and after the collision is zero, so angular momentum is conserved if you choose planet `A` as the axis.
The only difference with planet `B` as axis is that `r` is smaller by a factor of two, so all the angular momenta are halved. Even though the angular momenta are different than the ones calculated by planet `A`, angular momentum is still conserved.
The earth spins on its own axis once a day, but simultaneously travels in its circular one-year orbit around the sun, so any given part of it traces out a complicated loopy path. It would seem difficult to calculate the earth's angular momentum, but it turns out that there is an intuitively appealing shortcut: we can simply add up the angular momentum due to its spin plus that arising from its center of mass's circular motion around the sun. This is a special case of the following general theorem:
the spin theorem
An object's angular momentum with respect to some outside axis `A` can be found by adding up two parts:
(1) The first part is the object's angular momentum found by using its own center of mass as the axis, i.e., the angular momentum the object has because it is spinning.
(2) The other part equals the angular momentum that the object would have with respect to the axis `A` if it had all its mass concentrated at and moving with its center of mass.
Example 5: A system with its center of mass at rest
In the special case of an object whose center of mass is at rest, the spin theorem implies that the object's angular momentum is the same regardless of what axis we choose. (This is an even stronger statement than the choice of axis theorem, which only guarantees that angular momentum is conserved for any given choice of axis, without specifying that it is the same for all such choices.)
Example 6: Angular momentum of a rigid object
`=>` A motorcycle wheel has almost all its mass concentrated at the outside. If the wheel has mass `m` and radius `r`, and the time required for one revolution is `T`, what is the spin part of its angular momentum?
`=>` This is an example of the commonly encountered special case of rigid motion, as opposed to the rotation of a system like a hurricane in which the different parts take different amounts of time to go around. We don't really have to go through a laborious process of adding up contributions from all the many parts of a wheel, because they are all at about the same distance from the axis, and are all moving around the axis at about the same speed. The velocity is all perpendicular to the spokes,
`v_(bot)=v`
`="circumference"/T`
`=2pir"/"T`,
and the angular momentum of the wheel about its center is
`L=mv_(bot)r`
`=m(2pir"/"T)r`
`=2pimr^2"/"T`.
Note that although the factors of `2pi` in this expression is peculiar to a wheel with its mass concentrated on the rim, the proportionality to `m"/"T` would have been the same for any other rigidly rotating object. Although an object with a noncircular shape does not have a radius, it is also true in general that angular momentum is proportional to the square of the object's size for fixed values of mm and `T`. For instanceb doubling an object's size doubles both the `v_(bot)` and `r` factors in the contribution of each of its parts to the total angular momentum, resulting in an overall factor of four increase.
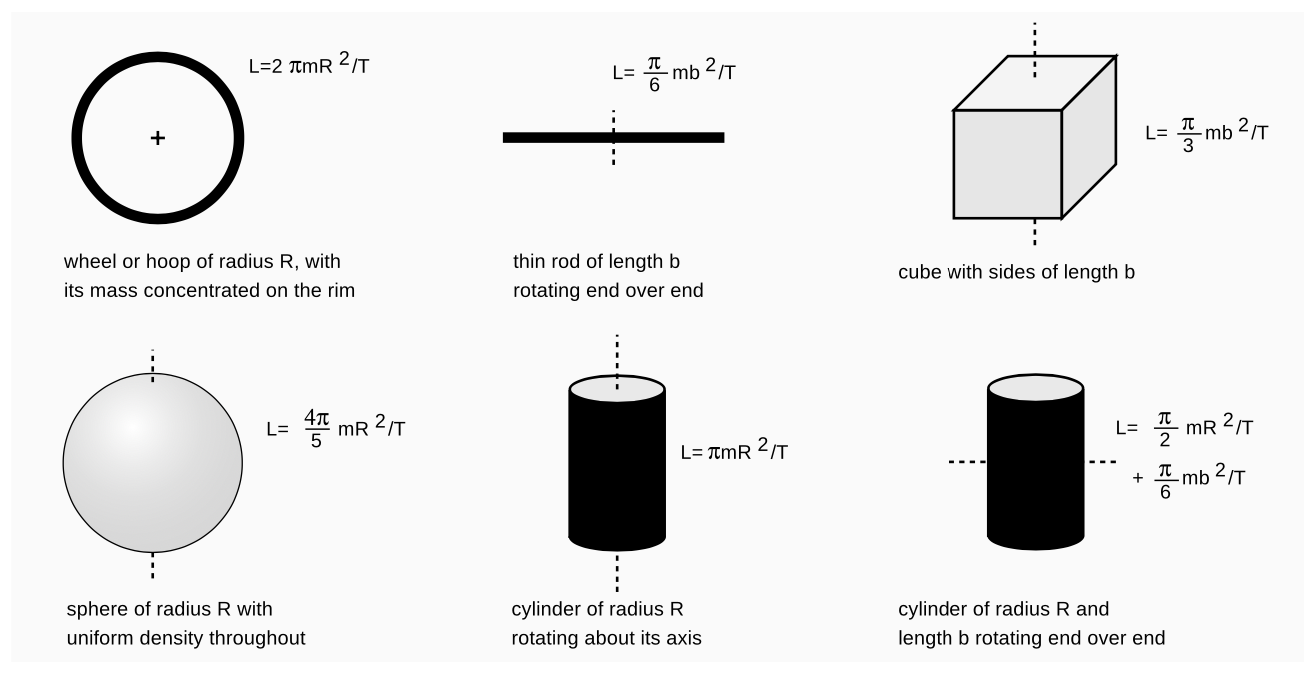
The figure shows some examples of angular momenta of various shapes rotating about their centers of mass. The equations for their angular momenta were derived using calculus, as described in my calculus-based book Simple Nature. Do not memorize these equations!
Example 7: The hammer throw
`=>` In the men's Olympic hammer throw, a steel ball of radius 6.1 cm is swung on the end of a wire of length 1.22 m. What fraction of the ball's angular momentum comes from its rotation, as opposed to its motion through space?
`=>` It's always important to solve problems symbolically first, and plug in numbers only at the end, so let the radius of the ball be `b`, and the length of the wire `ℓ`. If the time the ball takes to go once around the circle is `T`, then this is also the time it takes to revolve once around its own axis. Its speed is `v=2piℓ"/"T`, so its angular momentum due to its motion through space is `mvl=2piℓ^2"/"T`. Its angular momentum due to its rotation around its own center is `(4pi"/"5)mb^2"/"T`. The ratio of these two angular momenta is `(2"/"5)(b"/"ℓ)^2=1.0×10^(-3)`. The angular momentum due to the ball's spin is extremely small.
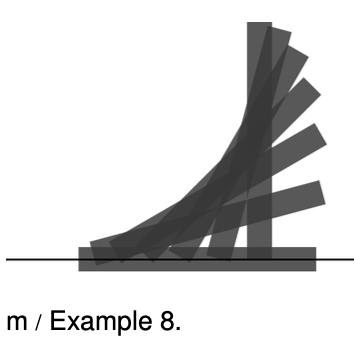 Example 8: Toppling a rod
Example 8: Toppling a rod
`=>` A rod of length `b` and mass `m` stands upright. We want to strike the rod at the bottom, causing it to fall and land flat. Find the momentum, `p`, that should be delivered, in terms of `m`, `b`, and `g`. Can this really be done without having the rod scrape on the floor?
`=>` This is a nice example of a question that can very nearly be answered based only on units. Since the three variables, `m`, `b`, and `g`, all have different units, they can't be added or subtracted. The only way to combine them mathematically is by multiplication or division. Multiplying one of them by itself is exponentiation, so in general we expect that the answer must be of the form
`p=Am^jb^kg^l`,
where `A`, `j`, `k`, and `l` are unitless constants. The result has to have units of `kg*m"/"s`. To get kilograms to the first power, we need
`j=1`,
meters to the first power requires
`k+l=1`,
and seconds to the power `-1` implies
`l=1/2`.
We find `j=1`, `k=1"/"2`, and `l=1"/"2`, so the solution must be of the form
`p=Amsqrt(bg)`.
Note that no physics was required!
Consideration of units, however, won't help us to find the unitless constant `A`. Let `t` be the time the rod takes to fall, so that `(1"/"2)"gt"^2=b"/"2`. If the rod is going to land exactly on its side, then the number of revolutions it completes while in the air must be 1/4, or 3/4, or 5/4, ..., but all the possibilities greater than 1/4 would cause the head of the rod to collide with the floor prematurely. The rod must therefore rotate at a rate that would cause it to complete a full rotation in a time `T=4t`, and it has angular momentum `L=(pi"/"6)mb^2"/"T`.
The momentum lost by the object striking the rod is `p`, and by conservation of momentum, this is the amount of momentum, in the horizontal direction, that the rod acquires. In other words, the rod will fly forward a little. However, this has no effect on the solution to the problem. More importantly, the object striking the rod loses angular momentum `bp"/"2`, which is also transferred to the rod. Equating this to the expression above for `L`, we find `p=(pi"/"12)msqrt(bg)`.
Finally, we need to know whether this can really be done without having the foot of the rod scrape on the floor. The figure shows that the answer is no for this rod of finite width, but it appears that the answer would be yes for a sufficiently thin rod. This is analyzed further in homework problem 28 on page 419.
Discussion Question
A In the example of the colliding asteroids, suppose planet `A` was moving toward the top of the page, at the same speed as the bottom asteroid. How would planet `A`'s astronomers describe the angular momenta of the asteroids? Would angular momentum still be conserved?
15.3 Two theorems about angular momentum by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.