14.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
momentum — a measure of motion, equal to `mv` for material objects
collision — an interaction between moving objects that lasts for a certain time
center of mass — the balance point or average position of the mass in a system
Notation
cm — center of mass, as in `x_"cm", a_"cm"`, etc.
Other Notation
impulse, `I`, `J` — the amount of momentum transferred, `Deltap`
elastic collision — one in which no `KE` is converted into other forms of energy
inelastic collision — one in which some `KE` is converted to other forms of energy
Summary
If two objects interact via a force, Newton's third law guarantees that any change in one's velocity vector will be accompanied by a change in the other's which is in the opposite direction. Intuitively, this means that if the two objects are not acted on by any external force, they cannot cooperate to change their overall state of motion. This can be made quantitative by saying that the quantity `m_1v_1+m_2v_2` must remain constant as long as the only forces are the internal ones between the two objects. This is a conservation law, called the conservation of momentum, and like the conservation of energy, it has evolved over time to include more and more phenomena unknown at the time the concept was invented. The momentum of a material object is
but this is more like a standard for comparison of momenta rather than a definition. For instance, light has momentum, but has no mass, and the above equation is not the right equation for light. The law of conservation of momentum says that the total momentum of any closed system, i.e., the vector sum of the momentum vectors of all the things in the system, is a constant.
An important application of the momentum concept is to collisions, i.e., interactions between moving objects that last for a certain amount of time while the objects are in contact or near each other. Conservation of momentum tells us that certain outcomes of a collision are impossible, and in some cases may even be sufficient to predict the motion after the collision. In other cases, conservation of momentum does not provide enough equations to find all the unknowns. In some collisions, such as the collision of a superball with the floor, very little kinetic energy is converted into other forms of energy, and this provides one more equation, which may suffice to predict the outcome.
The total momentum of a system can be related to its total mass and the velocity of its center of mass by the equation
`p_"total"=m_"total"v_"cm"`.
The center of mass, introduced on an intuitive basis in book 1 as the “balance point” of an object, can be generalized to any system containing any number of objects, and is defined mathematically as the weighted average of the positions of all the parts of all the objects,
`x_"cm"=(m_1x_1+m_2x_2...)/(m_1+m_2+...)`,
with similar equations for the `y` and `z` coordinates.
The frame of reference moving with the center of mass of a closed system is always a valid inertial frame, and many problems can be greatly simplified by working them in the inertial frame. For example, any collision between two objects appears in the c.m. frame as a head-on one-dimensional collision.
When a system is not closed, the rate at which momentum is transferred in or out is simply the total force being exerted externally on the system. If the force is constant,
`F_"total"=(dp_"total")/dt`
When the force is not constant, the force equals the slope of the tangent line on a graph of `p` versus `t`, and the change in momentum equals the area under the `F-t` graph.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. Derive a formula expressing the kinetic energy of an object in terms of its momentum and mass. `sqrt`
2. Two people in a rowboat wish to move around without causing the boat to move. What should be true about their total momentum? Explain.
3. A learjet traveling due east at 300 mi/hr collides with a jumbo jet which was heading southwest at 150 mi/hr. The jumbo jet's mass is five times greater than that of the learjet. When they collide, the learjet sticks into the fuselage of the jumbo jet, and they fall to earth together. Their engines stop functioning immediately after the collision. On a map, what will be the direction from the location of the collision to the place where the wreckage hits the ground? (Give an angle.) `sqrt`
4. A bullet leaves the barrel of a gun with a kinetic energy of 90 J. The gun barrel is 50 cm long. The gun has a mass of 4 kg, the bullet 10 g.
(a) Find the bullet's final velocity. `sqrt`
(b) Find the bullet's final momentum. `sqrt`
(c) Find the momentum of the recoiling gun.
(d) Find the kinetic energy of the recoiling gun, and explain why the recoiling gun does not kill the shooter. `sqrt`
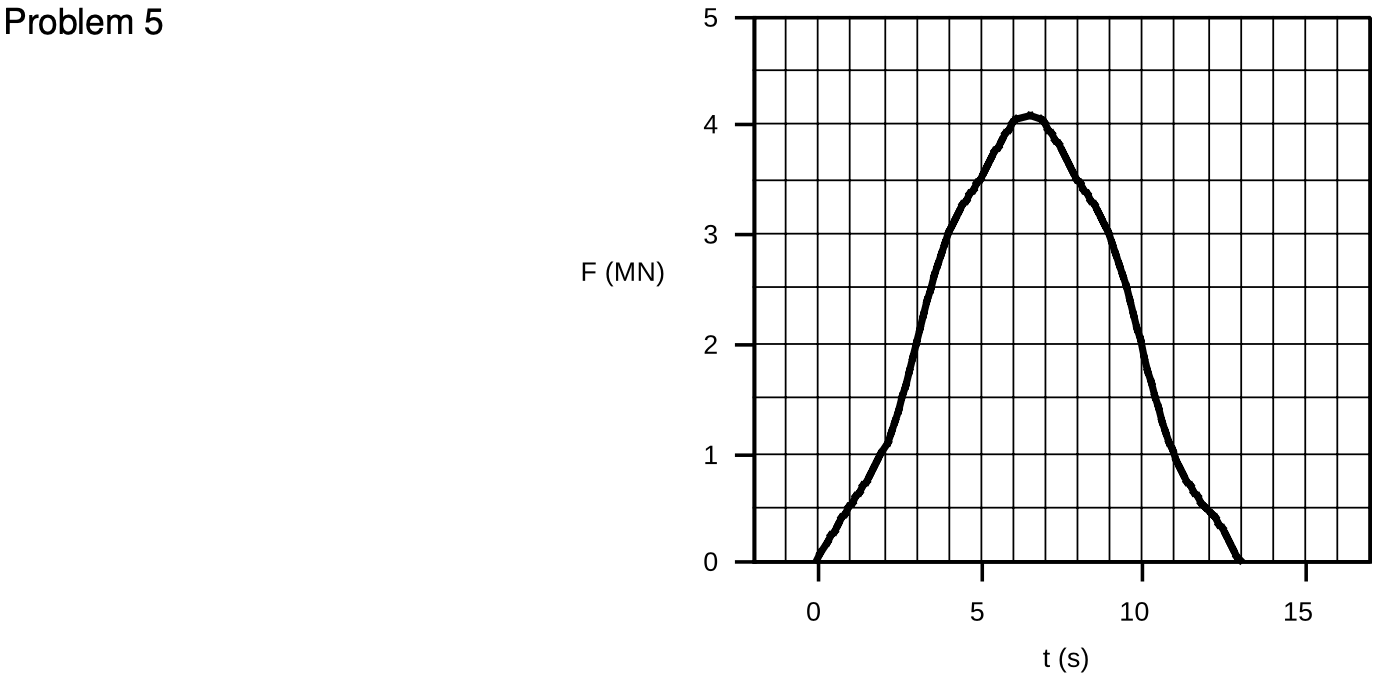
6. Cosmic rays are particles from outer space, mostly protons and atomic nuclei, that are continually bombarding the earth. Most of them, although they are moving extremely fast, have no discernible effect even if they hit your body, because their masses are so small. Their energies vary, however, and a very small minority of them have extremely large energies. In some cases the energy is as much as several Joules, which is comparable to the KE of a well thrown rock! If you are in a plane at a high altitude and are so incredibly unlucky as to be hit by one of these rare ultra-high-energy cosmic rays, what would you notice, the momentum imparted to your body, the energy dissipated in your body as heat, or both? Base your conclusions on numerical estimates, not just random speculation. (At these high speeds, one should really take into account the deviations from Newtonian physics described by Einstein's special theory of relativity. Don't worry about that, though.)
7. Show that for a body made up of many equal masses, the equation for the center of mass becomes a simple average of all the positions of the masses.
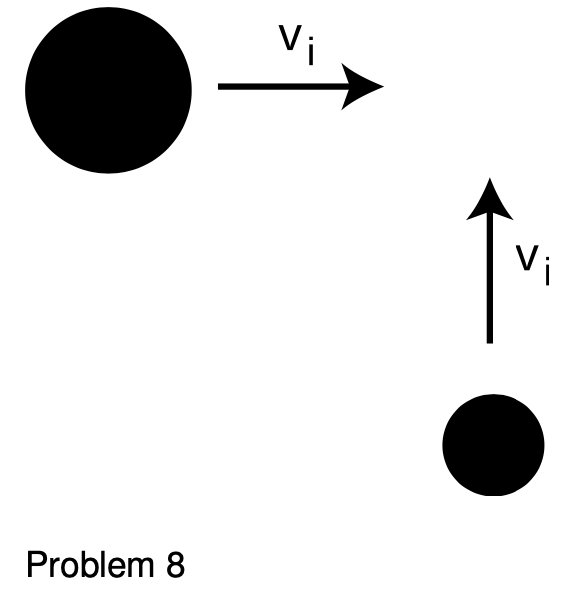 8. The figure shows a view from above of a collision about to happen between two air hockey pucks sliding without friction. They have the same speed, `v_i`, before the collision, but the big puck is 2.3 times more massive than the small one. Their sides have sticky stuff on them, so when they collide, they will stick together. At what angle will they emerge from the collision? In addition to giving a numerical answer, please indicate by drawing on the figure how your angle is defined.
8. The figure shows a view from above of a collision about to happen between two air hockey pucks sliding without friction. They have the same speed, `v_i`, before the collision, but the big puck is 2.3 times more massive than the small one. Their sides have sticky stuff on them, so when they collide, they will stick together. At what angle will they emerge from the collision? In addition to giving a numerical answer, please indicate by drawing on the figure how your angle is defined.
9. A flexible rope of mass `m` and length `L` slides without friction over the edge of a table. Let `x` be the length of the rope that is hanging over the edge at a given moment in time.
(a) Show that `x` satisfies the equation of motion `d^2x"/"dt^2=gx"/"L`. [Hint: Use `F=dp"/"dt`, which allows you to handle the two parts of the rope separately even though mass is moving out of one part and into the other.]
(b) Give a physical explanation for the fact that a larger value of `x` on the right-hand side of the equation leads to a greater value of the acceleration on the left side.
(c) When we take the second derivative of the function `x(t)` we are supposed to get essentially the same function back again, except for a constant out in front. The function `e^x` has the property that it is unchanged by differentiation, so it is reasonable to look for solutions to this problem that are of the form `x=be^(ct)`, where`b` and `c` are constants. Show that this does indeed provide a solution for two specific values of `c` (and for any value of `b`).
(d) Show that the sum of any two solutions to the equation of motion is also a solution.
(e) Find the solution for the case where the rope starts at rest at `t=0` with some nonzero value of `x`. `int` `***`
10. A very massive object with velocity `v` collides head-on with an object at rest whose mass is very small. No kinetic energy is converted into other forms. Prove that the low-mass object recoils with velocity `2v`. [Hint: Use the center-of-mass frame of reference.]
11. When the contents of a refrigerator cool down, the changed molecular speeds imply changes in both momentum and energy. Why, then, does a fridge transfer power through its radiator coils, but not force?
12. A 10-kg bowling ball moving at 2.0 m/s hits a 1.0-kg bowling pin, which is initially at rest. The other pins are all gone already, and the collision is head-on, so that the motion is one-dimensional. Assume that negligible amounts of heat and sound are produced. Find the velocity of the pin immediately after the collision.
13. A rocket ejects exhaust with an exhaust velocity `u`. The rate at which the exhaust mass is used (mass per unit time) is `b`. We assume that the rocket accelerates in a straight line starting from rest, and that no external forces act on it. Let the rocket's initial mass (fuel plus the body and payload) be `m_i`, and `m_f` be its final mass, after all the fuel is used up. (a) Find the rocket's final velocity, `v`, in terms of `u`, `m_i`, and `m_f`. Neglect the effects of special relativity. (b) A typical exhaust velocity for chemical rocket engines is 4000 m/s. Estimate the initial mass of a rocket that could accelerate a one-ton payload to 10% of the speed of light, and show that this design won't work. (For the sake of the estimate, ignore the mass of the fuel tanks. The speed is fairly small compared to `c`, so it's not an unreasonable approximation to ignore relativity.) `sqrt` `int` `***`
14. A firework shoots up into the air, and just before it explodes it has a certain momentum and kinetic energy. What can you say about the momenta and kinetic energies of the pieces immediately after the explosion? [Based on a problem from PSSC Physics.]
15. Suppose a system consisting of pointlike particles has a total kinetic energy `K_"cm"` measured in the center-of-mass frame of reference. Since they are pointlike, they cannot have any energy due to internal motion.
(a) Prove that in a different frame of reference, moving with velocity `u` relative to the center-of-mass frame, the total kinetic energy equals `K_"cm"+M|u|^2"/"2`, where `M` is the total mass. [Hint: You can save yourself a lot of writing if you express the total kinetic energy using the dot product.]
(b) Use this to prove that if energy is conserved in one frame of reference, then it is conserved in every frame of reference. The total energy equals the total kinetic energy plus the sum of the potential energies due to the particles' interactions with each other, which we assume depends only on the distance between particles. [For a simpler numerical example, see problem 13 on p. 306.] `***`
16. The big difference between the equations for momentum and kinetic energy is that one is proportional to `v` and one to `v^2`. Both, however, are proportional to `m`. Suppose someone tells you that there's a third quantity, funkosity, defined as `f=m^2v`, and that funkosity is conserved. How do you know your leg is being pulled?
17. A mass `m` moving at velocity `v` collides with a stationary target having the same mass `m`. Find the maximum amount of energy that can be released as heat and sound. `sqrt`
18. Two blobs of putty collide head-on. The collision is completely symmetric: the blobs are of equal mass, and they collide at equal speeds. What becomes of the energy the blobs had before the collision? The momentum?
14.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.