13.5 Work and potential energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
13.5 Work and potential energy
The techniques for calculating work can also be applied to the calculation of potential energy. If a certain force depends only on the distance between the two participating objects, then the energy released by changing the distance between them is defined as the potential energy, and the amount of potential energy lost equals minus the work done by the force,
`DeltaPE=-W`.
The minus sign occurs because positive work indicates that the potential energy is being expended and converted to some other form.
It is sometimes convenient to pick some arbitrary position as a reference position, and derive an equation for once and for all that gives the potential energy relative to this position
`PE_x=-W_(ref->x).`[potential energy at a point x]
To find the energy transferred into or out of potential energy, one then subtracts two different values of this equation.
These equations might almost make it look as though work and energy were the same thing, but they are not. First, potential energy measures the energy that a system has stored in it, while work measures how much energy is transferred in or out. Second, the techniques for calculating work can be used to find the amount of energy transferred in many situations where there is no potential energy involved, as when we calculate the amount of kinetic energy transformed into heat by a car's brake shoes.
Example 6: A toy gun
`=>` A toy gun uses a spring with a spring constant of 10 N/m to shoot a ping-pong ball of mass 5 g. The spring is compressed to 10 cm shorter than its equilibrium length when the gun is loaded. At what speed is the ball released?
`=>` The equilibrium point is the natural choice for a reference point. Using the equation found previously for the work, we have
`PE_x=1/2k(x-x_o)^2`.
The spring loses contact with the ball at the equilibrium point, so the final potential energy is
`PE_f=0`.
The initial potential energy is
`PE_i=1/2(10 N"/"m)(0.10 m)^2.`
`=0.05 J`
The loss in potential energy of 0.05 J means an increase in kinetic energy of the same amount. The velocity of the ball is found by solving the equation `KE=1"/"2mv^2` for `v`,
`v=sqrt((2KE)/m)`
`=sqrt("(2)(0.05 J)"/(0.005 kg))`
`=4 m"/"s.`
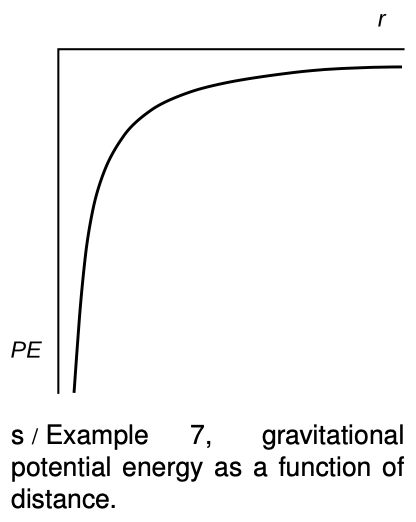 Example 7: Gravitational potential energy
Example 7: Gravitational potential energy
`=>` We have already found the equation `DeltaPE=-FDeltay` for the gravitational potential energy when the change in height is not enough to cause a significant change in the gravitational force `F`. What if the change in height is enough so that this assumption is no longer valid? Use the equation derived in section 13.4 to find the potential energy, using `r=infty` as a reference point.
`=>` The potential energy equals minus the work that would have to be done to bring the object from `r_1=infty` to `r=r_2`, which is
This is simpler than the equation for the work, which is an example of why it is advantageous to record an equation for potential energy relative to some reference point, rather than an equation for work.
Although the equations derived in the previous two examples may seem arcane and not particularly useful except for toy designers and rocket scientists, their usefulness is actually greater than it appears. The equation for the potential energy of a spring can be adapted to any other case in which an object is compressed, stretched, twisted, or bent. While you are not likely to use the equation for gravitational potential energy for anything practical, it is directly analogous to an equation that is extremely useful in chemistry, which is the equation for the potential energy of an electron at a distance `r` from the nucleus of its atom. As discussed in more detail later in the course, the electrical force between the electron and the nucleus is proportional to `1"/"r^2`, just like the gravitational force between two masses. Since the equation for the force is of the same form, so is the equation for the potential energy.

Discussion Questions
A What does the graph of `PE=(1/2)k(x-x_o)^2` look like as a function of `x`? Discuss the physical significance of its features.
B What does the graph of `PE=-(GMm)/r` look like as a function of r? Discuss the physical significance of its features. How would the equation and graph change if some other reference point was chosen rather than `r=infty`?
C Starting at a distance `r` from a planet of mass `M`, how fast must an object be moving in order to have a hyperbolic orbit, i.e., one that never comes back to the planet? This velocity is called the escape velocity. Interpreting the result, does it matter in what direction the velocity is? Does it matter what mass the object has? Does the object escape because it is moving too fast for gravity to act on it?
D Does a spring have an “escape velocity?”
E Calculus-based question: If the form of energy being transferred is potential energy, then the equations `F=dW"/"dx` and `W=intFdx` become `F=-dPE"/"dx` and `PE=-intFdx`. How would you then apply the following calculus concepts: zero derivative at minima and maxima, and the second derivative test for concavity up or down.
13.5 Work and potential energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.