13.2 Work in three dimensions by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
13.2 Work in three dimensions
A force perpendicular to the motion does no work.
Suppose work is being done to change an object's kinetic energy. A force in the same direction as its motion will speed it up, and a force in the opposite direction will slow it down. As we have already seen, this is described as doing positive work or doing negative work on the object. All the examples discussed up until now have been of motion in one dimension, but in three dimensions the force can be at any angle ? with respect to the direction of motion.
What if the force is perpendicular to the direction of motion? We have already seen that a force perpendicular to the motion results in circular motion at constant speed. The kinetic energy does not change, and we conclude that no work is done when the force is perpendicular to the motion.
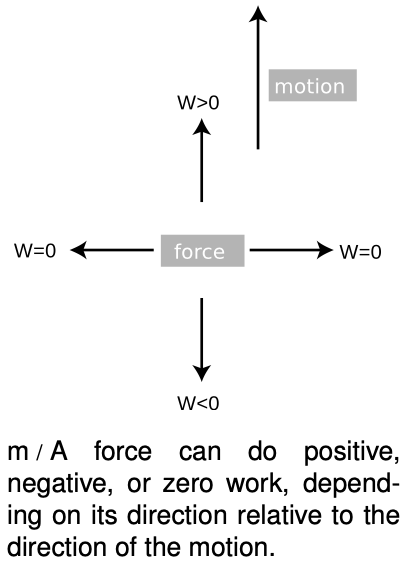 So far we have been reasoning about the case of a single force acting on an object, and changing only its kinetic energy. The result is more generally true, however. For instance, imagine a hockey puck sliding across the ice. The ice makes an upward normal force, but does not transfer energy to or from the puck.
So far we have been reasoning about the case of a single force acting on an object, and changing only its kinetic energy. The result is more generally true, however. For instance, imagine a hockey puck sliding across the ice. The ice makes an upward normal force, but does not transfer energy to or from the puck.
Forces at other angles
where the vector `d` is simply a less cumbersome version of the notation `Deltar`. This result can be rewritten via trigonometry as
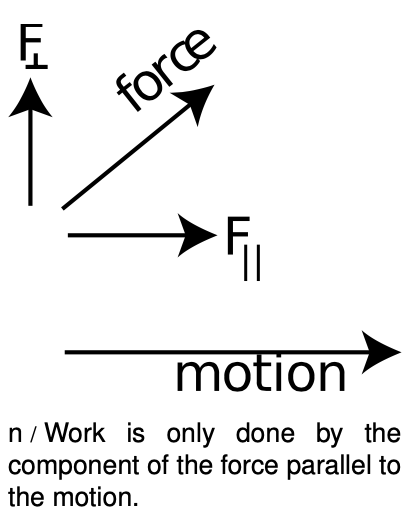 `W=|F||d|costheta`. [work done by a constant force]
`W=|F||d|costheta`. [work done by a constant force]
Even though this equation has vectors in it, it depends only on their magnitudes, and the magnitude of a vector is a scalar. Work is therefore still a scalar quantity, which only makes sense if it is defined as the transfer of energy. Ten gallons of gasoline have the ability to do a certain amount of mechanical work, and when you pull in to a full-service gas station you don't have to say “Fill 'er up with 10 gallons of south-going gas.”
Students often wonder why this equation involves a cosine rather than a sine, or ask if it would ever be a sine. In vector addition, the treatment of sines and cosines seemed more equal and democratic, so why is the cosine so special now? The answer is that if we are going to describe, say, a velocity vector, we must give both the component parallel to the `x` axis and the component perpendicular to the `x` axis (i.e., the `y` component). In calculating work, however, the force component perpendicular to the motion is irrelevant --- it changes the direction of motion without increasing or decreasing the energy of the object on which it acts. In this context, it is only the parallel force component that matters, so only the cosine occurs.
 self-check:
self-check:
(a) Work is the transfer of energy. According to this definition, is the horse in the picture doing work on the pack? (b) If you calculate work by the method described in this section, is the horse in figure o doing work on the pack?
(answer in the back of the PDF version of the book)
Example 3: Pushing a broom
`=>` If you exert a force of 21 N on a push broom, at an angle 35 degrees below horizontal, and walk for 5.0 m, how much work do you do? What is the physical significance of this quantity of work?
`=>` Using the second equation above, the work done equals
`(21 N)(5.0 m)(cos35°)=86 J.`
The form of energy being transferred is heat in the floor and the broom's bristles. This comes from the chemical energy stored in your body. (The majority of the calories you burn are dissipated directly as heat inside your body rather than doing any work on the broom. The 86 J is only the amount of energy transferred through the broom's handle.)
Example 4: A violin
As a violinist draws the bow across a string, the bow hairs exert both a normal force and a kinetic frictional force on the string. The normal force is perpendicular to the direction of motion, and does no work. However, the frictional force is in the same direction as the motion of the bow, so it does work: energy is transferred to the string, causing it to vibrate.
One way of playing a violin more loudly is to use longer strokes. Since , the greater distance results in more work.
A second way of getting a louder sound is to press the bow more firmly against the strings. This increases the normal force, and although the normal force itself does no work, an increase in the normal force has the side effect of increasing the frictional force, thereby increasing .
The violinist moves the bow back and forth, and sound is produced on both the “up-bow” (the stroke toward the player's left) and the “down-bow” (to the right). One may, for example, play a series of notes in alternation between up-bows and down-bows. However, if the notes are of unequal length, the up and down motions tend to be unequal, and if the player is not careful, she can run out of bow in the middle of a note! To keep this from happening, one can move the bow more quickly on the shorter notes, but the resulting increase in `d` will make the shorter notes louder than they should be. A skilled player compensates by reducing the force.
13.2 Work in three dimensions by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.