13.1 Work: the transfer of mechanical energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
13.1 Work: the transfer of mechanical energy
The concept of work
The mass contained in a closed system is a conserved quantity, but if the system is not closed, we also have ways of measuring the amount of mass that goes in or out. The water company does this with a meter that records your water use.
Likewise, we often have a system that is not closed, and would like to know how much energy comes in or out. Energy, however, is not a physical substance like water, so energy transfer cannot be measured with the same kind of meter. How can we tell, for instance, how much useful energy a tractor can “put out” on one tank of gas?
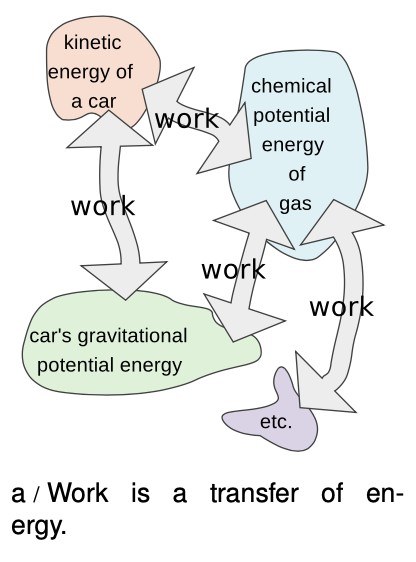 The law of conservation of energy guarantees that all the chemical energy in the gasoline will reappear in some form, but not necessarily in a form that is useful for doing farm work. Tractors, like cars, are extremely inefficient, and typically 90% of the energy they consume is converted directly into heat, which is carried away by the exhaust and the air flowing over the radiator. We wish to distinguish the energy that comes out directly as heat from the energy that serves to accelerate a trailer or to plow a field, so we define a technical meaning of the ordinary word “work” to express the distinction:
The law of conservation of energy guarantees that all the chemical energy in the gasoline will reappear in some form, but not necessarily in a form that is useful for doing farm work. Tractors, like cars, are extremely inefficient, and typically 90% of the energy they consume is converted directly into heat, which is carried away by the exhaust and the air flowing over the radiator. We wish to distinguish the energy that comes out directly as heat from the energy that serves to accelerate a trailer or to plow a field, so we define a technical meaning of the ordinary word “work” to express the distinction:
definition of work
Work is the amount of energy transferred into or out of a system, not counting energy transferred by heat conduction.
self-check:
 Based on this definition, is work a vector, or a scalar? What are its units?
Based on this definition, is work a vector, or a scalar? What are its units?
The conduction of heat is to be distinguished from heating by friction. When a hot potato heats up your hands by conduction, the energy transfer occurs without any force, but when friction heats your car's brake shoes, there is a force involved. The transfer of energy with and without a force are measured by completely different methods, so we wish to include heat transfer by frictional heating under the definition of work, but not heat transfer by conduction. The definition of work could thus be restated as the amount of energy transferred by forces.
Calculating work as force multiplied by distance
 The examples in figures
b-
d show that there are many different ways in which
energy can be transferred. Even so, all these examples have two things in common:
The examples in figures
b-
d show that there are many different ways in which
energy can be transferred. Even so, all these examples have two things in common:
- A force is involved.
- The tractor travels some distance as it does the work.
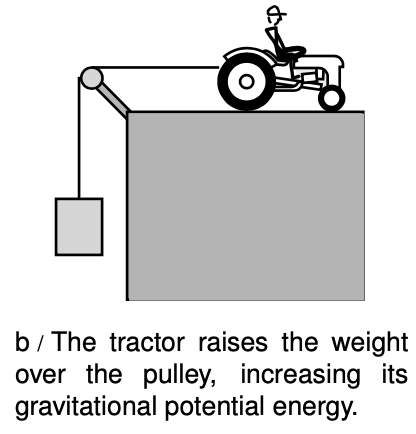
In b, the increase in the height of the weight, `Deltay`, is the same as the distance the tractor travels, which we'll call `d`. For simplicity, we discuss the 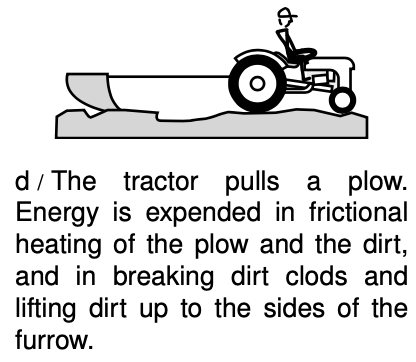 case where the tractor raises the weight at constant speed, so that there is no change in the kinetic energy of the weight, and we assume that there is negligible friction in the pulley, so that the force the tractor applies to the rope is the same as the rope's upward force on the weight. By Newton's first law, these forces are also of the same magnitude as the earth's gravitational force on the weight. The increase in the weight's potential energy is given by `FDeltay`, so the work done by the tractor on the weight equals `Fd`, the product of the force and the distance moved:
case where the tractor raises the weight at constant speed, so that there is no change in the kinetic energy of the weight, and we assume that there is negligible friction in the pulley, so that the force the tractor applies to the rope is the same as the rope's upward force on the weight. By Newton's first law, these forces are also of the same magnitude as the earth's gravitational force on the weight. The increase in the weight's potential energy is given by `FDeltay`, so the work done by the tractor on the weight equals `Fd`, the product of the force and the distance moved:
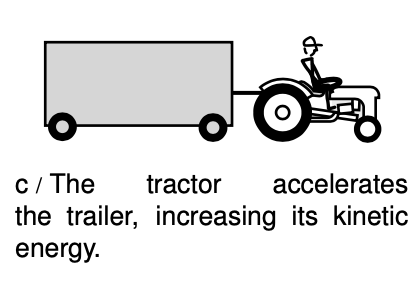
In example c, the tractor's force on the trailer accelerates it, increasing its kinetic energy. If frictional forces on the trailer are negligible, then the increase in the trailer's kinetic energy can be found using the same algebra that was used on page 313 to find the potential energy due to gravity. Just as in example b, we have
.
Does this equation always give the right answer? Well, sort of. In example d, there are two quantities of work you might want to calculate: the work done by the tractor on the plow and the work done by the plow on the dirt. These two quantities can't both equal `Fd`. Most of the energy transmitted through the cable goes into frictional heating of the plow and the dirt. The work done by the plow on the dirt is less than the work done by the tractor on the plow, by an amount equal to the heat absorbed by the plow. It turns out that the equation gives the work done by the tractor, not the work done by the plow. How are you supposed to know when the equation will work and when it won't? The somewhat complex answer is postponed until section 13.6. Until then, we will restrict ourselves to examples in which `W=Fd` gives the right answer; essentially the reason the ambiguities come up is that when one surface is slipping past another, `d` may be hard to define, because the two surfaces move different distances.
 We have also been using examples in which the force is in the same direction as the motion, and the force is constant. (If the force was not constant, we would have to represent it with a function, not a symbol that stands for a number.) To summarize, we have:
We have also been using examples in which the force is in the same direction as the motion, and the force is constant. (If the force was not constant, we would have to represent it with a function, not a symbol that stands for a number.) To summarize, we have:
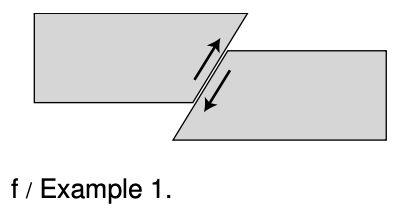 Example 1: Mechanical work done in an earthquake
Example 1: Mechanical work done in an earthquake
`=>` In 1998, geologists discovered evidence for a big prehistoric earthquake in Pasadena, between 10,000 and 15,000 years ago. They found that the two sides of the fault moved 6.7 m relative to one another, and estimated that the force between them was `1.3` x `10^17 N`. How much energy was released?
`=>` Multiplying the force by the distance gives `9` x `10^17 J`. For comparison, the Northridge earthquake of 1994, which killed 57 people and did 40 billion dollars of damage, released 22 times less energy.
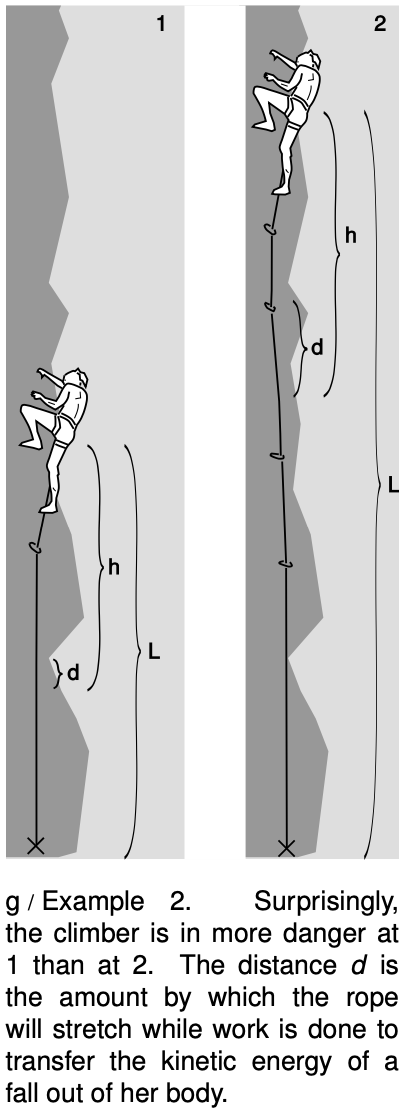 Example 2: The fall factor
Example 2: The fall factor
Counterintuitively, the rock climber may be in more danger in figure g/1 than later when she gets up to position g/2.
Along her route, the climber has placed removable rock anchors (not shown) and carabiners attached to the anchors. She clips the rope into each carabiner so that it can travel but can't pop out. In both 1 and 2, she has ascended a certain distance above her last anchor, so that if she falls, she will drop through a height `h` that is about twice this distance, and this fall height is about the same in both cases. In fact, `h` is somewhat larger than twice her height above the last anchor, because the rope is intentionally designed to stretch under the big force of a falling climber who suddenly brings it taut.
To see why we want a stretchy rope, consider the equation `F=W"/"d` in the case where `d` is zero; `F` would theoretically become infinite. In a fall, the climber loses a fixed amount of gravitational energy `mgh`. This is transformed into an equal amount of kinetic energy as she falls, and eventually this kinetic energy has to be transferred out of her body when the rope comes up taut. If the rope was not stretchy, then the distance traveled at the point where the rope attaches to her harness would be zero, and the force exerted would theoretically be infinite. Before the rope reached the theoretically infinite tension `F` it would break (or her back would break, or her anchors would be pulled out of the rock). We want the rope to be stretchy enough to make `d` fairly big, so that dividing `W` by `d` gives a small force.
In g/1 and g/2, the fall `h` is about the same. What is different is the length `L` of rope that has been paid out. A longer rope can stretch more, so the distance `d` traveled after the “catch” is proportional to `L`. Combining `F=W"/"d`, `Wproph`, and `dpropL` , we have `Fproph"/"L`. For these reasons, rock climbers define a fall factor `f=h"/"L`. The larger fall factor in g/1 is more dangerous.
Machines can increase force, but not work.
Figure h shows a pulley arrangement for doubling the force supplied by the tractor (book 1, section 5.6). The tension in the left-hand rope is equal throughout, assuming negligible friction, so there are two forces pulling the pulley to the left, each equal to the original force exerted by the tractor on the rope. This doubled force is transmitted through the right-hand rope to the stump.

It might seem as though this arrangement would also double the work done by the tractor, but look again. As the tractor moves forward 2 meters, 1 meter of rope comes around the pulley, and the pulley moves 1 m to the left. Although the pulley exerts double the force on the stump, the pulley and stump only move half as far, so the work done on the stump is no greater that it would have been without the pulley.
The same is true for any mechanical arrangement that increases or decreases force, such as the gears on a ten-speed bike. You can't get out more work than you put in, because that would violate conservation of energy. If you shift gears so that your force on the pedals is amplified, the result is that you just have to spin the pedals more times.
No work is done without motion.
It strikes most students as nonsensical when they are told that if they stand still and hold a heavy bag of cement, they are doing no work on the bag. Even if it makes sense mathematically that gives zero when `d` is zero, it seems to violate common sense. You would certainly become tired! The solution is simple. Physicists have taken over the common word “work” and given it a new technical meaning, which is the transfer of energy. The energy of the bag of cement is not changing, and that is what the physicist means by saying no work is done on the bag.
 There is a transformation of energy, but it is taking place entirely within your own muscles, which are converting chemical energy into heat. Physiologically, a human muscle is not like a tree limb, which can support a weight indefinitely without the expenditure of energy. Each muscle cell's contraction is generated by zillions of little molecular machines, which take turns supporting the tension. When a particular molecule goes on or off duty, it moves, and since it moves while exerting a force, it is doing work. There is work, but it is work done by one molecule in a muscle cell on another.
There is a transformation of energy, but it is taking place entirely within your own muscles, which are converting chemical energy into heat. Physiologically, a human muscle is not like a tree limb, which can support a weight indefinitely without the expenditure of energy. Each muscle cell's contraction is generated by zillions of little molecular machines, which take turns supporting the tension. When a particular molecule goes on or off duty, it moves, and since it moves while exerting a force, it is doing work. There is work, but it is work done by one molecule in a muscle cell on another.
Positive and negative work
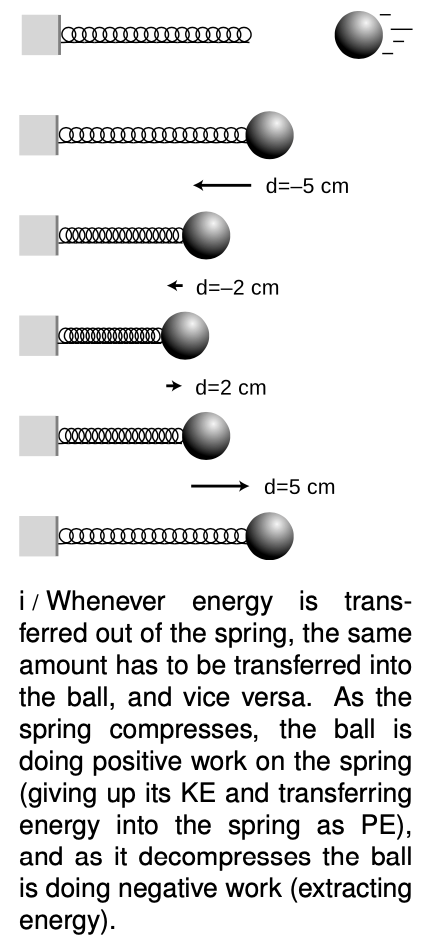
When object A transfers energy to object B, we say that A does positive work on B. B is said to do negative work on A. In other words, a machine like a tractor is defined as doing positive work. This use of the plus and minus signs relates in a logical and consistent way to their use in indicating the directions of force and motion in one dimension. In figure i, suppose we choose a coordinate system with the `x` axis pointing to the right. Then the force the spring exerts on the ball is always a positive number. The ball's motion, however, changes directions. The symbol `d` is really just a shorter way of writing the familiar quantity `Deltax`, whose positive and negative signs indicate direction.
While the ball is moving to the left, we use `d<0` to represent its direction of motion, and the work done by the spring, `Fd`, comes out negative. This indicates that the spring is taking kinetic energy out of the ball, and accepting it in the form of its own potential energy.
As the ball is reaccelerated to the right, it has `d>0`, `Fd` is positive, and the spring does positive work on the ball. Potential energy is transferred out of the spring and deposited in the ball as kinetic energy.
In summary:
rule for calculating work (including cases of negative work)
The work done by a force can be calculated as
`W = Fd`,
if the force is constant and along the same line as the motion. The quantity `d` is to be interpreted as a synonym for `Deltax`, i.e., positive and negative signs are used to indicate the direction of motion. Some ambiguities are encountered in cases such as kinetic friction.
self-check:
 In figure i, what about the work done by the ball on the spring?
In figure i, what about the work done by the ball on the spring?
[4]
There are many examples where the transfer of energy out of an object cancels out the transfer of energy in. When the tractor pulls the plow with a rope, the rope does negative work on the tractor and positive work on the plow. The total work done by the rope is zero, which makes sense, since it is not changing its energy.
It may seem that when your arms do negative work by lowering a bag of cement, the cement is not really transferring energy into your body. If your body was storing potential energy like a compressed spring, you would be able to raise and lower a weight all day, recycling the same energy. The bag of cement does transfer energy into your body, but your body accepts it as heat, not as potential energy. The tension in the muscles that control the speed of the motion also results in the conversion of chemical energy to heat, for the same physiological reasons discussed previously in the case where you just hold the bag still.
One of the advantages of electric cars over gasoline-powered cars is that it is just as easy to put energy back in a battery as it is to take energy out. When you step on the brakes in a gas car, the brake shoes do negative work on the rest of the car. The kinetic energy of the car is transmitted through the brakes and accepted by the brake shoes in the form of heat. The energy cannot be recovered. Electric cars, however, are designed to use regenerative braking. The brakes don't use friction at all. They are electrical, and when you step on the brake, the negative work done by the brakes means they accept the energy and put it in the battery for later use. 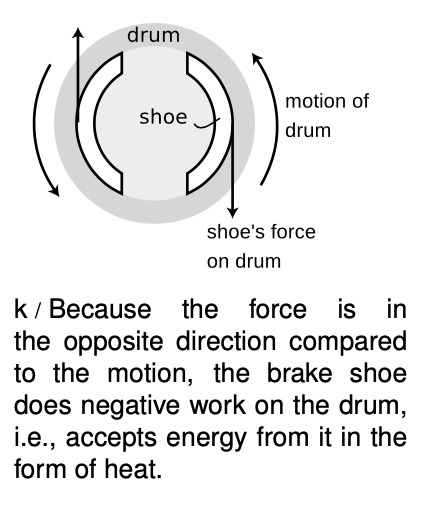 This is one of the reasons why an electric car is far better for the environment than a gas car, even if the ultimate source of the electrical energy happens to be the burning of oil in the electric company's plant. The electric car recycles the same energy over and over, and only dissipates heat due to air friction and rolling resistance, not braking. (The electric company's power plant can also be fitted with expensive pollution-reduction equipment that would be prohibitively expensive or bulky for a passenger car.)
This is one of the reasons why an electric car is far better for the environment than a gas car, even if the ultimate source of the electrical energy happens to be the burning of oil in the electric company's plant. The electric car recycles the same energy over and over, and only dissipates heat due to air friction and rolling resistance, not braking. (The electric company's power plant can also be fitted with expensive pollution-reduction equipment that would be prohibitively expensive or bulky for a passenger car.)
Discussion Questions
A Besides the presence of a force, what other things differentiate the processes of frictional heating and heat conduction?
B Criticize the following incorrect statement: “A force doesn't do any work unless it's causing the object to move.”
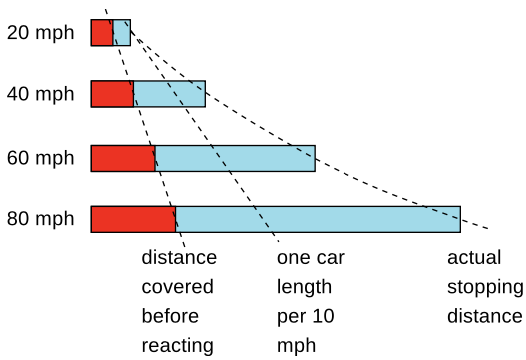 C To stop your car, you must first have time to react, and then it takes some time for the car to slow down. Both of these times contribute to the distance you will travel before you can stop. The figure shows how the average stopping distance increases with speed. Because the stopping distance increases more and more rapidly as you go faster, the rule of one car length per 10 m.p.h. of speed is not conservative enough at high speeds. In terms of work and kinetic energy, what is the reason for the more rapid increase at high speeds?
C To stop your car, you must first have time to react, and then it takes some time for the car to slow down. Both of these times contribute to the distance you will travel before you can stop. The figure shows how the average stopping distance increases with speed. Because the stopping distance increases more and more rapidly as you go faster, the rule of one car length per 10 m.p.h. of speed is not conservative enough at high speeds. In terms of work and kinetic energy, what is the reason for the more rapid increase at high speeds?
13.1 Work: the transfer of mechanical energy by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
