12.4 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
potential energy — the energy having to do with the distance between two objects that interact via a noncontact force
Notation
`PE` — potential energy
Other Notation
`U` or `V` — symbols used for potential energy in the scientific literature and in most advanced textbooks
Summary
Historically, the energy concept was only invented to include a few phenomena, but it was later generalized more and more to apply to new situations, for example nuclear reactions. This generalizing process resulted in an undesirably long list of types of energy, each of which apparently behaved according to its own rules.
The first step in simplifying the picture came with the realization that heat was a form of random motion on the atomic level, i.e., heat was nothing more than the kinetic energy of atoms.
A second and even greater simplification was achieved with the realization that all the other apparently mysterious forms of energy actually had to do with changing the distances between atoms (or similar processes in nuclei). This type of energy, which relates to the distance between objects that interact via a force, is therefore of great importance. We call it potential energy.
Most of the important ideas about potential energy can be understood by studying the example of gravitational potential energy. The change in an object's gravitational potential energy is given by
`DeltaPE_{grav} = -F_{grav} Deltay`, [if `F_{grav}` is constant, i.e., the motion is all near the Earth's surface]
The most important thing to understand about potential energy is that there is no unambiguous way to define it in an absolute sense. The only thing that everyone can agree on is how much the potential energy has changed from one moment in time to some later moment in time.
Homework Problems
Key
`sqrt` A computerized check is available online.
`int` A problem that requires calculus.
`***` A difficult problem
1. Can gravitational potential energy ever be negative? Note that the question refers to `PE`, not `DeltaPE`, so that you must think about how the choice of a reference level comes into play. [Based on a problem by Serway and Faughn.]
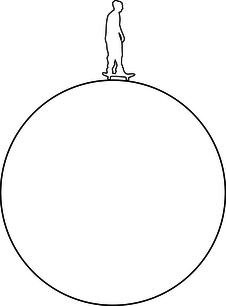
h / Problem 7.
2. A ball rolls up a ramp, turns around, and comes back down. When does it have the greatest gravitational potential energy? The greatest kinetic energy? [Based on a problem by Serway and Faughn.]
3. (a) You release a magnet on a tabletop near a big piece of iron, and the magnet leaps across the table to the iron. Does the magnetic potential energy increase, or decrease? Explain. (b) Suppose instead that you have two repelling magnets. You give them an initial push towards each other, so they decelerate while approaching each other. Does the magnetic potential energy increase, or decrease? Explain.
4. Let `E_b` be the energy required to boil one kg of water. (a) Find an equation for the minimum height from which a bucket of water must be dropped if the energy released on impact is to vaporize it. Assume that all the heat goes into the water, not into the dirt it strikes, and ignore the relatively small amount of energy required to heat the water from room temperature to `100°C`. [Numerical check, not for credit: Plugging in `E_b=2.3 MJ"/"kg` should give a result of 230 km.] `sqrt`
(b) Show that the units of your answer in part a come out right based on the units given for `E_b`.
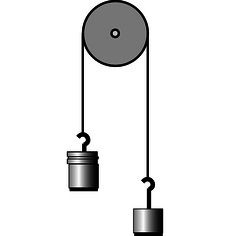
i / Problem 17.
5. A grasshopper with a mass of 110 mg falls from rest from a height of 310 cm. On the way down, it dissipates 1.1 mJ of heat due to air resistance. At what speed, in m/s, does it hit the ground? (solution in the pdf version of the book)
6. A person on a bicycle is to coast down a ramp of height `h` and then pass through a circular loop of radius `r`. What is the smallest value of `h` for which the cyclist will complete the loop without falling? (Ignore the kinetic energy of the spinning wheels.) `sqrt`
7. A skateboarder starts at rest nearly at the top of a giant cylinder, and begins rolling down its side. (If he started exactly at rest and exactly at the top, he would never get going!) Show that his board loses contact with the pipe after he has dropped by a height equal to one third the radius of the pipe. `***`
8. (a) A circular hoop of mass `m` and radius`r` spins like a wheel while its center remains at rest. Its period (time required for one revolution) is `T`. Show that its kinetic energy equals `(2pi^2mr^2)"/"T^2`.
(b) If such a hoop rolls with its center moving at velocity `v`, its kinetic energy equals `(1"/"2)mv^2`, plus the amount of kinetic energy found in the first part of this problem. Show that a hoop rolls down an inclined plane with half the acceleration that a frictionless sliding block would have. `***`
9. (solution in the pdf version of the book) Students are often tempted to think of potential energy and kinetic energy as if they were always related to each other, like yin and yang. To show this is incorrect, give examples of physical situations in which (a) PE is converted to another form of PE, and (b) KE is converted to another form of KE.
10. Lord Kelvin, a physicist, told the story of how he encountered James Joule when Joule was on his honeymoon. As he traveled, Joule would stop with his wife at various waterfalls, and measure the difference in temperature between the top of the waterfall and the still water at the bottom. (a) It would surprise most people to learn that the temperature increased. Why should there be any such effect, and why would Joule care? How would this relate to the energy concept, of which he was the principal inventor? (b) How much of a gain in temperature should there be between the top and bottom of a 50-meter waterfall? (c) What assumptions did you have to make in order to calculate your answer to part b? In reality, would the temperature change be more than or less than what you calculated? [Based on a problem by Arnold Arons.] `sqrt`
11. Make an order-of-magnitude estimate of the power represented by the loss of gravitational energy of the water going over Niagara Falls. If the hydroelectric plant at the bottom of the falls could convert 100% of this to electrical power, roughly how many households could be powered? (solution in the pdf version of the book)
12. When you buy a helium-filled balloon, the seller has to inflate it from a large metal cylinder of the compressed gas. The helium inside the cylinder has energy, as can be demonstrated for example by releasing a little of it into the air: you hear a hissing sound, and that sound energy must have come from somewhere. The total amount of energy in the cylinder is very large, and if the valve is inadvertently damaged or broken off, the cylinder can behave like a bomb or a rocket.
Suppose the company that puts the gas in the cylinders prepares cylinder A with half the normal amount of pure helium, and cylinder B with the normal amount. Cylinder B has twice as much energy, and yet the temperatures of both cylinders are the same. Explain, at the atomic level, what form of energy is involved, and why cylinder B has twice as much.
13. At a given temperature, the average kinetic energy per molecule is a fixed value, so for instance in air, the more massive oxygen molecules are moving more slowly on the average than the nitrogen molecules. The ratio of the masses of oxygen and nitrogen molecules is 16.00 to 14.01. Now suppose a vessel containing some air is surrounded by a vacuum, and the vessel has a tiny hole in it, which allows the air to slowly leak out. The molecules are bouncing around randomly, so a given molecule will have to “try” many times before it gets lucky enough to head out through the hole. Find the rate at which oxygen leaks divided by the rate at which nitrogen leaks. (Define this rate according to the fraction of the gas that leaks out in a given time, not the mass or number of molecules leaked per unit time.) `sqrt`
14. Explain in terms of conservation of energy why sweating cools your body, even though the sweat is at the same temperature as your body. Describe the forms of energy involved in this energy transformation. Why don't you get the same cooling effect if you wipe the sweat off with a towel? Hint: The sweat is evaporating.
15. Anya and Ivan lean over a balcony side by side. Anya throws a penny downward with an initial speed of 5 m/s. Ivan throws a penny upward with the same speed. Both pennies end up on the ground below. Compare their kinetic energies and velocities on impact.
16. (a) A circular hoop of mass `m` and radius`r` spins like a wheel while its center remains at rest. Let `omega` (Greek letter omega) be the number of radians it covers per unit time, i.e., `omega=2?"/"T`, where the period, `T`, is the time for one revolution. Show that its kinetic energy equals `(1"/"2)momega^2r^2`.
(b) Show that the answer to part a has the right units. (Note that radians aren't really units, since the definition of a radian is a unitless ratio of two lengths.)
(c) If such a hoop rolls with its center moving at velocity`v`, its kinetic energy equals `(1"/"2)mv^2`, plus the amount of kinetic energy found in part a. Show that a hoop rolls down an inclined plane with half the acceleration that a frictionless sliding block would have.
17. The figure shows two unequal masses, `M` and `m`, connected by a string running over a pulley. This system was analyzed previously in problem 10 on p. 181, using Newton's laws.
(a) Analyze the system using conservation of energy instead. Find the speed the weights gain after being released from rest and traveling a distance `h`. `sqrt`
(b) Use your result from part a to find the acceleration, reproducing the result of the earlier problem. `sqrt`
12.4 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.