10.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
ellipse — a flattened circle; one of the conic sections
conic section — a curve formed by the intersection of a plane and an infinite cone
hyperbola — another conic section; it does not close back on itself
period — the time required for a planet to complete one orbit; more generally, the time for one repetition of some repeating motion
focus — one of two special points inside an ellipse: the ellipse consists of all points such that the sum of the distances to the two foci equals a certain number; a hyperbola also has a focus
Notation
`G` — the constant of proportionality in Newton's law of gravity; the of attraction between two 1-kg spheres at a center-to-center distance of 1 m
Summary
Kepler deduced three empirical laws from data on the motion of the planets:
- Kepler's elliptical orbit law: The planets orbit the sun in elliptical orbits with the sun at one focus.
- Kepler's equal-area law: The line connecting a planet to the sun sweeps out equal areas in equal amounts of time.
- Kepler's law of periods: The time required for a planet to orbit the sun is proportional to the long axis of the ellipse raised to the 3/2 power. The constant of proportionality is the same for all the planets.
Newton was able to find a more fundamental explanation for these laws. Newton's law of gravity states that the magnitude of the attractive force between any two objects in the universe is given by .
Weightlessness of objects in orbit around the earth is only apparent. An astronaut inside a spaceship is simply falling along with the spaceship. Since the spaceship is falling out from under the astronaut, it appears as though there was no gravity accelerating the astronaut down toward the deck.
Gravitational forces, like all other forces, add like vectors. A gravitational force such as we ordinarily feel is the vector sum of all the forces exerted by all the parts of the earth. As a consequence of this, Newton proved the shell theorem for gravitational forces:
If an object lies outside a thin, uniform shell of mass, then the vector sum of all the gravitational forces exerted by all the parts of the shell is the same as if all the shell's mass was concentrated at its center. If the object lies inside the shell, then all the gravitational forces cancel out exactly.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. Roy has a mass of 60 kg. Laurie has a mass of 65 kg. They are 1.5 m apart.
(a) What is the magnitude of the gravitational force of the earth on Roy?
(b) What is the magnitude of Roy's gravitational force on the earth?
(c) What is the magnitude of the gravitational force between Roy and Laurie?
(d) What is the magnitude of the gravitational force between Laurie and the sun? `sqrt`
2. During a solar eclipse, the moon, earth and sun all lie on the same line, with the moon between the earth and sun. Define your coordinates so that the earth and moon lie at greater `x` values than the sun. For each force, give the correct sign as well as the magnitude. (a) What force is exerted on the moon by the sun? (b) On the moon by the earth? (c) On the earth by the sun? (d) What total force is exerted on the sun? (e) On the moon? (f) On the earth? `sqrt`
3. Suppose that on a certain day there is a crescent moon, and you can tell by the shape of the crescent that the earth, sun and moon form a triangle with a `135°` interior angle at the moon's corner. What is the magnitude of the total gravitational force of the earth and the sun on the moon? (If you haven't done problem 2 already, you might want to try it first, since it's easier, and some of its results can be recycled in this problem.) `sqrt`

4. How high above the Earth's surface must a rocket be in order to have 1/100 the weight it would have at the surface? Express your answer in units of the radius of the Earth. `sqrt`
5. The star Lalande 21185 was found in 1996 to have two planets in roughly circular orbits, with periods of 6 and 30 years. What is the ratio of the two planets' orbital radii? `sqrt`
6. In a Star Trek episode, the Enterprise is in a circular orbit around a planet when something happens to the engines. Spock then tells Kirk that the ship will spiral into the planet's surface unless they can fix the engines. Is this scientifically correct? Why?
7. (a) Suppose a rotating spherical body such as a planet has a radius `r` and a uniform density `?`, and the time required for one rotation is `T`. At the surface of the planet, the apparent acceleration of a falling object is reduced by the acceleration of the ground out from under it. Derive an equation for the apparent acceleration of gravity, `g`, at the equator in terms of `r`, `rho`, `T`, and `G`.`sqrt`
(b) Applying your equation from a, by what fraction is your apparent weight reduced at the equator compared to the poles, due to the Earth's rotation? `sqrt`
(c) Using your equation from a, derive an equation giving the value of `T` for which the apparent acceleration of gravity becomes zero, i.e., objects can spontaneously drift off the surface of the planet. Show that `T` only depends on `rho`, and not on `r`. `sqrt`
(d) Applying your equation from c, how long would a day have to be in order to reduce the apparent weight of objects at the equator of the Earth to zero? [Answer: 1.4 hours]
(e) Astronomers have discovered objects they called pulsars, which emit bursts of radiation at regular intervals of less than a second. If a pulsar is to be interpreted as a rotating sphere beaming out a natural “searchlight” that sweeps past the earth with each rotation, use your equation from c to show that its density would have to be much greater than that of ordinary matter.
(f) Astrophysicists predicted decades ago that certain stars that used up their sources of energy could collapse, forming a ball of neutrons with the fantastic density of `10^17 kg"/"m^3`. If this is what pulsars really are, use your equation from c to explain why no pulsar has ever been observed that flashes with a period of less than 1 ms or so.
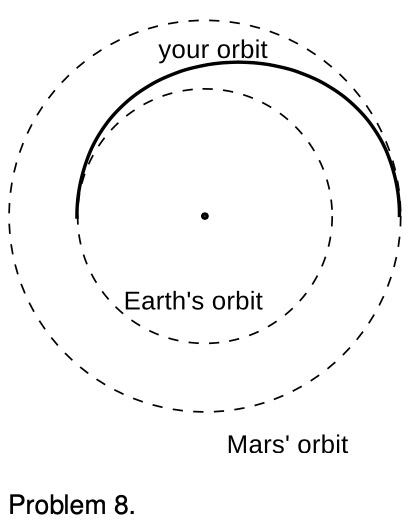 8. You are considering going on a space voyage to Mars, in which your route would be half an ellipse, tangent to the Earth's orbit at one end and tangent to Mars' orbit at the other. Your spacecraft's engines will only be used at the beginning and end, not during the voyage. How long would the outward leg of your trip last? (Assume the orbits of Earth and Mars are circular.) `sqrt`
8. You are considering going on a space voyage to Mars, in which your route would be half an ellipse, tangent to the Earth's orbit at one end and tangent to Mars' orbit at the other. Your spacecraft's engines will only be used at the beginning and end, not during the voyage. How long would the outward leg of your trip last? (Assume the orbits of Earth and Mars are circular.) `sqrt`
9. (a) If the earth was of uniform density, would your weight be increased or decreased at the bottom of a mine shaft? Explain.
(b) In real life, objects weigh slightly more at the bottom of a mine shaft. What does that allow us to infer about the Earth? `***`
10. Ceres, the largest asteroid in our solar system, is a spherical body with a mass 6000 times less than the earth's, and a radius which is 13 times smaller. If an astronaut who weighs 400 N on earth is visiting the surface of Ceres, what is her weight?
11. Prove, based on Newton's laws of motion and Newton's law of gravity, that all falling objects have the same acceleration if they are dropped at the same location on the earth and if other forces such as friction are unimportant. Do not just say, it's constant.” You are supposed to be proving that `g` should be the same number for all objects.
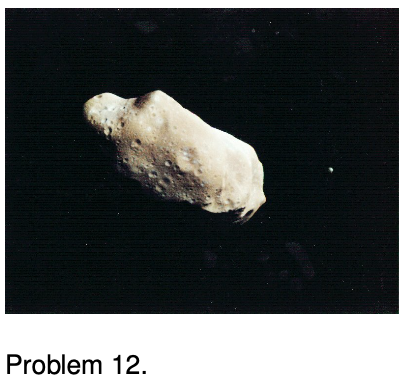 12. The figure shows an image from the Galileo space probe taken during its August 1993 flyby of the asteroid Ida. Astronomers were surprised when Galileo detected a smaller object orbiting Ida. This smaller object, the only known satellite of an asteroid in our solar system, was christened Dactyl, after the mythical creatures who lived on Mount Ida, and who protected the infant Zeus. For scale, Ida is about the size and shape of Orange County, and Dactyl the size of a college campus. Galileo was unfortunately unable to measure the time, `T`, required for Dactyl to orbit Ida. If it had, astronomers would have been able to make the first accurate determination of the mass and density of an asteroid. Find an equation for the density, `rho`, of Ida in terms of Ida's known volume, `V`, the known radius, `r`, of Dactyl's orbit, and the lamentably unknown variable `T`. (This is the same technique that was used successfully for determining the masses and densities of the planets that have moons.)
12. The figure shows an image from the Galileo space probe taken during its August 1993 flyby of the asteroid Ida. Astronomers were surprised when Galileo detected a smaller object orbiting Ida. This smaller object, the only known satellite of an asteroid in our solar system, was christened Dactyl, after the mythical creatures who lived on Mount Ida, and who protected the infant Zeus. For scale, Ida is about the size and shape of Orange County, and Dactyl the size of a college campus. Galileo was unfortunately unable to measure the time, `T`, required for Dactyl to orbit Ida. If it had, astronomers would have been able to make the first accurate determination of the mass and density of an asteroid. Find an equation for the density, `rho`, of Ida in terms of Ida's known volume, `V`, the known radius, `r`, of Dactyl's orbit, and the lamentably unknown variable `T`. (This is the same technique that was used successfully for determining the masses and densities of the planets that have moons.)
13. If a bullet is shot straight up at a high enough velocity, it will never return to the earth. This is known as the escape velocity. We will discuss escape velocity using the concept of energy later in the course, but it can also be gotten at using straightforward calculus. In this problem, you will analyze the motion of an object of mass `m` whose initial velocity is exactly equal to escape velocity. We assume that it is starting from the surface of a spherically symmetric planet of mass `M` and radius `b`. The trick is to guess at the general form of the solution, and then determine the solution in more detail. Assume (as is true) that the solution is of the form `r=kt^p`, where `r` is the object's distance from the center of the planet at time `t`, and `k` and `p` are constants.
(a) Find the acceleration, and use Newton's second law and Newton's law of gravity to determine `k` and `p`. You should find that the result is independent of `m`. `sqrt`
(b) What happens to the velocity as `t` approaches infinity?
(c) Determine escape velocity from the Earth's surface? `sqrt` `int`
14. Astronomers have recently observed stars orbiting at very high speeds around an unknown object near the center of our galaxy. For stars orbiting at distances of about `10^14 m` from the object, the orbital velocities are about `10^6 m"/"s`. Assuming the orbits are circular, estimate the mass of the object, in units of the mass of the sun, `2×10^30 kg`. If the object was a tightly packed cluster of normal stars, it should be a very bright source of light. Since no visible light is detected coming from it, it is instead believed to be a supermassive black hole. `sqrt`
15. Astronomers have detected a solar system consisting of three planets orbiting the star Upsilon Andromedae. The planets have been named b, c, and d. Planet b's average distance from the star is 0.059 A.U., and planet c's average distance is 0.83 A.U., where an astronomical unit or A.U. is defined as the distance from the Earth to the sun. For technical reasons, it is possible to determine the ratios of the planets' masses, but their masses cannot presently be determined in absolute units. Planet c's mass is 3.0 times that of planet b. Compare the star's average gravitational force on planet c with its average force on planet b. [Based on a problem by Arnold Arons.]
16. Some communications satellites are in orbits called geosynchronous: the satellite takes one day to orbit the earth from west to east, so that as the earth spins, the satellite remains above the same point on the equator. What is such a satellite's altitude above the surface of the earth?
17. As is discussed in more detail in example 3 on p. 390, tidal interactions with the earth are causing the moon's orbit to grow gradually larger. Laser beams bounced off of a mirror left on the moon by astronauts have allowed a measurement of the moon's rate of recession, which is about 1 cm per year. This means that the gravitational force acting between earth and moon is decreasing. By what fraction does the force decrease with each 27-day orbit? \hwhint{hwhint:receding-moon} [Based on a problem by Arnold Arons.]
18. Suppose that we inhabited a universe in which, instead of Newton's law of gravity, we had `F=ksqrt(m_1m_2)"/"r^2`, where `k` is some constant with different units than `G`. (The force is still attractive.) However, we assume that `a=F"/"m` and the rest of Newtonian physics remains true, and we use `a=F"/"m` to define our mass scale, so that, e.g., a mass of 2 kg is one which exhibits half the acceleration when the same force is applied to it as to a 1 kg mass.
(a) Is this new law of gravity consistent with Newton's third law?
(b) Suppose you lived in such a universe, and you dropped two unequal masses side by side. What would happen?
(c) Numerically, suppose a 1.0-kg object falls with an acceleration of `10 m"/"s^2`. What would be the acceleration of a rain drop with a mass of 0.1 g? Would you want to go out in the rain?
(d) If a falling object broke into two unequal pieces while it fell, what would happen?
(e) Invent a law of gravity that results in behavior that is the opposite of what you found in part b. [Based on a problem by Arnold Arons.]
19. (a) A certain vile alien gangster lives on the surface of an asteroid, where his weight is 0.20 N. He decides he needs to lose weight without reducing his consumption of princesses, so he's going to move to a different asteroid where his weight will be 0.10 N. The real estate agent's database has asteroids listed by mass, however, not by surface gravity. Assuming that all asteroids are spherical and have the same density, how should the mass of his new asteroid compare with that of his old one?
(b) Jupiter's mass is 318 times the Earth's, and its gravity is about twice Earth's. Is this consistent with the results of part a? If not, how do you explain the discrepancy?
20. Where would an object have to be located so that it would experience zero total gravitational force from the earth and moon? `sqrt`
 21. The planet Uranus has a mass of `8.68×10^25 kg` and a radius of `2.56×10^4 km`. The figure shows the relative sizes of Uranus and Earth.
21. The planet Uranus has a mass of `8.68×10^25 kg` and a radius of `2.56×10^4 km`. The figure shows the relative sizes of Uranus and Earth.
(a) Compute the ratio `g_U"/"g_E`, where `g_U` is the strength of the gravitational field at the surface of Uranus and `g_E` is the corresponding quantity at the surface of the Earth. `sqrt`
(b) What is surprising about this result? How do you explain it?
22. The International Space Station orbits at an average altitude of about 370 km above sea level. Compute the value of `g` at that altitude. `sqrt`
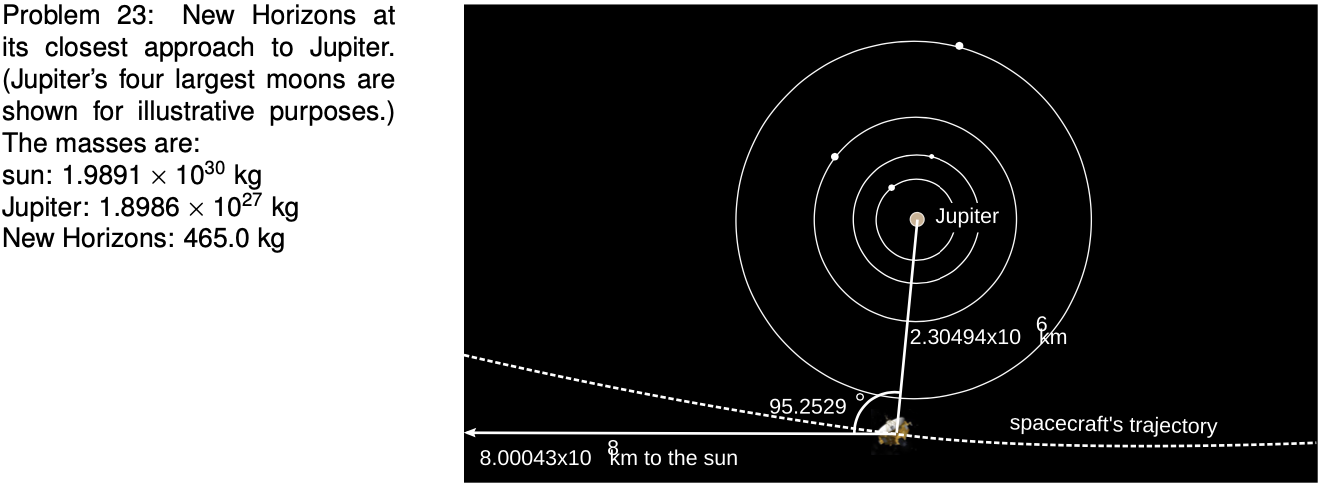
23. On Feb. 28, 2007, the New Horizons space probe, on its way to a 2015 flyby of Pluto, passed by the planet Jupiter for a gravity-assisted maneuver that increased its speed and changed its course. The dashed line in the figure shows the spacecraft's trajectory, which is curved because of three forces: the force of the exhaust gases from the probe's own engines, the sun's gravitational force, and Jupiter's gravitational force. Find the magnitude of the total gravitational force acting on the probe. You will find that the sun's force is much smaller than Jupiter's, so that the magnitude of the total force is determined almost entirely by Jupiter's force. However, this is a high-precision problem, and you will find that the total force is slightly different from Jupiter's https://www.vcalc.com/wiki/vCalc/Force. `sqrt`
24. On an airless body such as the moon, there is no atmospheric friction, so it should be possible for a satellite to orbit at a very low altitude, just high enough to keep from hitting the mountains. (a) Suppose that such a body is a smooth sphere of uniform density `rho` and radius `r`. Find the velocity required for a ground-skimming orbit. `sqrt`
(b) A typical asteroid has a density of about `2 g"/"cm^3`, i.e., twice that of water. (This is a lot lower than the density of the earth's crust, probably indicating that the low gravity is not enough to compact the material very tightly, leaving lots of empty space inside.) Suppose that it is possible for an astronaut in a spacesuit to jump at `2 m"/"s`. Find the radius of the largest asteroid on which it would be possible to jump into a ground-skimming orbit. `sqrt`
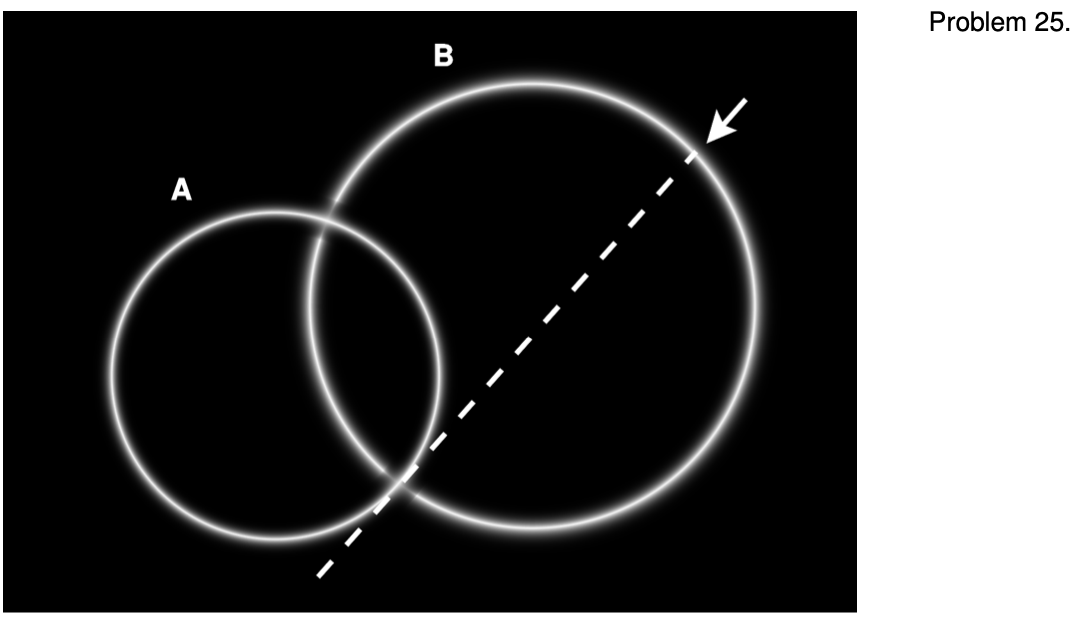 25. The figure shows a region of outer space in which two stars have exploded, leaving behind two overlapping spherical shells of gas, which we assume to remain at rest. The figure is a cross-section in a plane containing the shells' centers. A space probe is released with a very small initial speed at the point indicated by the arrow, initially moving in the direction indicated by the dashed line. Without any further information, predict as much as possible about the path followed by the probe and its changes in speed along that path. `***`
25. The figure shows a region of outer space in which two stars have exploded, leaving behind two overlapping spherical shells of gas, which we assume to remain at rest. The figure is a cross-section in a plane containing the shells' centers. A space probe is released with a very small initial speed at the point indicated by the arrow, initially moving in the direction indicated by the dashed line. Without any further information, predict as much as possible about the path followed by the probe and its changes in speed along that path. `***`
26. Approximate the earth's density as being constant. (a) Find the gravitational field at a point P inside the earth and half-way between the center and the surface. Express your result as a ratio `g_P"/"g_S` relative to the field we experience at the surface. (b) As a check on your answer, make sure that the same reasoning leads to a reasonable result when the fraction 1/2 is replaced by the value 0 (P being the earth's center) or the value 1 (P being a point on the surface).
27. The earth is divided into solid inner core, a liquid outer core, and a plastic mantle. Physical properties such as density change discontinuously at the boundaries between one layer and the next. Although the density is not completely constant within each region, we will approximate it as being so for the purposes of this problem. (We neglect the crust as well.) Let `R` be the radius of the earth as a whole and `M` its mass. The following table gives a model of some properties of the three layers, as determined by methods such as the observation of earthquake waves that have propagated from one side of the planet to the other.
| region | outer radius/`R` | mass/`M` |
| mantle | 1 | 0.69 |
| outer core | 0.55 | 0.29 |
| inner core | 0.19 | 0.017 |
The boundary between the mantle and the outer core is referred to as the Gutenberg discontinuity. Let `g_s` be the strength of the earth's gravitational field at its surface and `g_G` its value at the Gutenberg discontinuity. Find `g_G"/"g_s`. `sqrt`
Exercise 10: The shell theorem
This exercise is an approximate numerical test of the shell theorem. There are seven masses A-G, each being one kilogram. Masses A-F, each one meter from the center, form a shape like two Egyptian pyramids joined at their bases; this is a rough approximation to a six-kilogram spherical shell of mass. Mass G is five meters from the center of the main group. The class will divide into six groups and split up the work required in order to calculate the vector sum of the six gravitational forces exerted on mass G. Depending on the size of the class, more than one group may be assigned to deal with the contribution of the same mass to the total force, and the redundant groups can check each other's results.
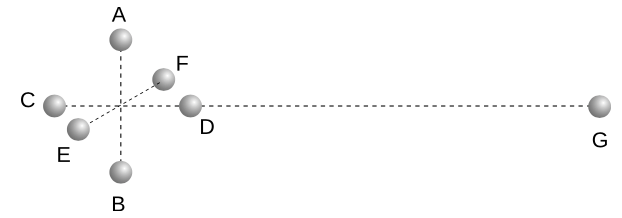 1. Discuss as a class what can be done to simplify the task of calculating the vector sum, and how to organize things so that each group can work in parallel with the others.
1. Discuss as a class what can be done to simplify the task of calculating the vector sum, and how to organize things so that each group can work in parallel with the others.
2. Each group should write its results on the board in units of pico-newtons, retaining five significant figures of precision. Everyone will need to use the same value for the gravitational constant, `G=6.6743×10^(-11) Ncdotm^2"/"kg^2`.
3. The class will determine the vector sum and compare with the result that would be obtained with the shell theorem.
10.8 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.