10.5 Weighing the earth by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
10.5 Weighing the earth
Let's look more closely at the application of Newton's law of gravity to objects on the earth's surface. Since the earth's gravitational force is the same as if its mass was all concentrated at its center, the force on a falling object of mass `m` is given by:
`F = G M_(earth) m "/" r_(earth)^2`
The object's acceleration equals `a=F"/"m`, so the object's mass cancels out and we get the same acceleration for all falling objects, as we knew we should:
 `g=GM_"earth""/"r_"earth"^2`.
`g=GM_"earth""/"r_"earth"^2`.
Newton knew neither the mass of the earth nor a numerical value for the constant `G`. But if someone could measure `G`, then it would be possible for the first time in history to determine the mass of the earth! The only way to measure `G` is to measure the gravitational force between two objects of known mass, but that's an exceedingly difficult task, because the force between any two objects of ordinary size is extremely small.
The English physicist Henry Cavendish was the first to succeed, using the apparatus shown in figures o and p. The two larger balls were lead spheres 8 inches in diameter, and each one attracted the small ball near it. The two small balls hung from the ends of a horizontal rod, which itself hung by a thin thread. The frame from which the larger balls hung could be rotated by hand about a vertical axis, so that for instance the large ball on the right would 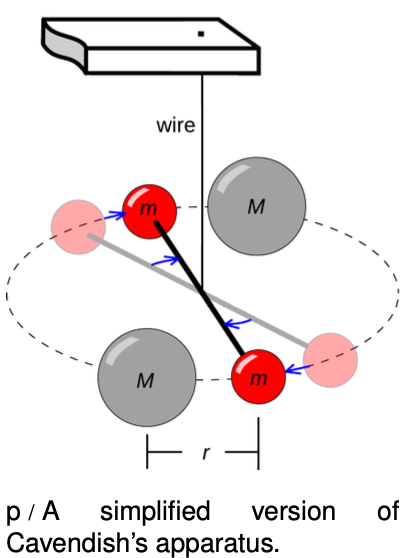 pull its neighboring small ball toward us and while the small ball on the left would be pulled away from us. The thread from which the small balls hung would thus be twisted through a small angle, and by calibrating the twist of the thread with known forces, the actual gravitational force could be determined. Cavendish set up the whole apparatus in a room of his house, nailing all the doors shut to keep air currents from disturbing the delicate apparatus. The results had to be observed through telescopes stuck through holes drilled in the walls. Cavendish's experiment provided the first numerical values for `G` and for the mass of the earth. The presently accepted value of `G` is `6.67×10^(-11) Ncdotm^2"/"kg^2`.
pull its neighboring small ball toward us and while the small ball on the left would be pulled away from us. The thread from which the small balls hung would thus be twisted through a small angle, and by calibrating the twist of the thread with known forces, the actual gravitational force could be determined. Cavendish set up the whole apparatus in a room of his house, nailing all the doors shut to keep air currents from disturbing the delicate apparatus. The results had to be observed through telescopes stuck through holes drilled in the walls. Cavendish's experiment provided the first numerical values for `G` and for the mass of the earth. The presently accepted value of `G` is `6.67×10^(-11) Ncdotm^2"/"kg^2`.
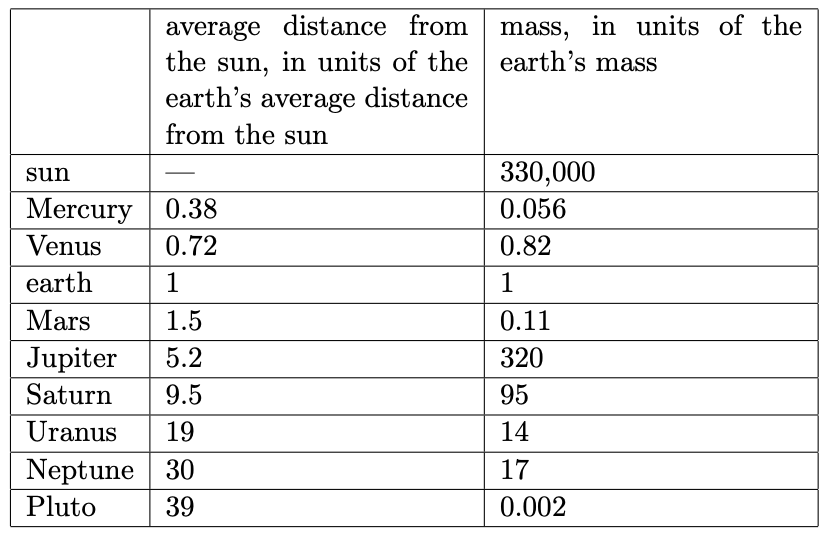
Knowing `G` not only allowed the determination of the earth's mass but also those of the sun and the other planets. For instance, by observing the acceleration of one of Jupiter's moons, we can infer the mass of Jupiter. The following table gives the distances of the planets from the sun and the masses of the sun and planets. (Other data are given in the back of the book.)
A It would have been difficult for Cavendish to start designing an experiment without at least some idea of the order of magnitude of `G`. How could he estimate it in advance to within a factor of 10?
B Fill in the details of how one would determine Jupiter's mass by observing the acceleration of one of its moons. Why is it only necessary to know the acceleration of the moon, not the actual force acting on it? Why don't we need to know the mass of the moon? What about a planet that has no moons, such as Venus --- how could its mass be found?
10.5 Weighing the earth by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.