10.4 Vector addition of gravitational forces by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
10.4 Vector addition of gravitational forces
Pick a flower on earth and you move the farthest star. -- Paul Dirac
When you stand on the ground, which part of the earth is pulling down on you with its gravitational force? Most people are tempted to say that the effect only comes from the part directly under you, since gravity always pulls straight down. Here are three observations that might help to change your mind:
- If you jump up in the air, gravity does not stop affecting you just because you are not touching the earth: gravity is a noncontact force. That means you are not immune from the gravity of distant parts of our planet just because you are not touching them.
- Gravitational effects are not blocked by intervening matter. For instance, in an eclipse of the moon, the earth is lined up directly between the sun and the moon, but only the sun's light is blocked from reaching the moon, not its gravitational force --- if the sun's gravitational force on the moon was blocked in this situation, astronomers would be able to tell because the moon's acceleration would change suddenly. A more subtle but more easily observable example is that the tides are caused by the moon's gravity, and tidal effects can occur on the side of the earth facing away from the moon. Thus, far-off parts of the earth are not prevented from attracting you with their gravity just because there is other stuff between you and them.
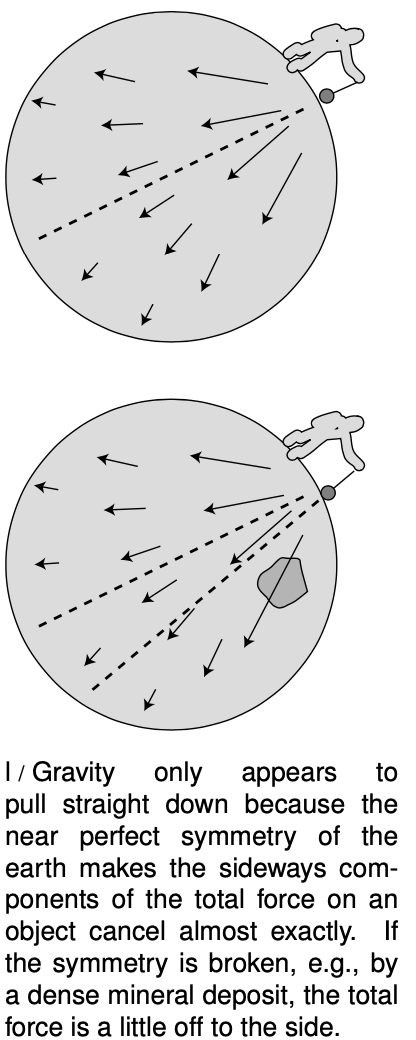 Prospectors sometimes search for underground deposits of dense minerals by measuring the direction of the local gravitational forces, i.e., the direction things fall or the direction a plumb bob hangs. For instance, the gravitational forces in the region to the west of such a deposit would point along a line slightly to the east of the earth's center. Just because the total gravitational force on you points down, that doesn't mean that only the parts of the earth directly below you are attracting you. It's just that the sideways components of all the force vectors acting on you come very close to canceling out.
Prospectors sometimes search for underground deposits of dense minerals by measuring the direction of the local gravitational forces, i.e., the direction things fall or the direction a plumb bob hangs. For instance, the gravitational forces in the region to the west of such a deposit would point along a line slightly to the east of the earth's center. Just because the total gravitational force on you points down, that doesn't mean that only the parts of the earth directly below you are attracting you. It's just that the sideways components of all the force vectors acting on you come very close to canceling out.
A cubic centimeter of lava in the earth's mantle, a grain of silica inside Mt. Kilimanjaro, and a flea on a cat in Paris are all attracting you with their gravity. What you feel is the vector sum of all the gravitational forces exerted by all the atoms of our planet, and for that matter by all the atoms in the universe.
When Newton tested his theory of gravity by comparing the orbital acceleration of the moon to the acceleration of a falling apple on earth, he assumed he could compute the earth's force on the apple using the distance from the apple to the earth's center. Was he wrong? After all, it isn't just the earth's center attracting the apple, it's the whole earth. A kilogram of dirt a few feet under his backyard in England would have a much greater force on the apple than a kilogram of molten rock deep under Australia, thousands of miles away. There's really no obvious reason why the force should come out right if you just pretend that the earth's whole mass is concentrated at its center. Also, we know that the earth has some parts that are more dense, and some parts that are less dense. The solid crust, on which we live, is considerably less dense than the molten rock on which it floats. By all rights, the computation of the vector sum of all the forces exerted by all the earth's parts should be a horrendous mess.
 Actually, Newton had sound reasons for treating the earth's mass as if it was concentrated at its center. First, although Newton no doubt suspected the earth's density was nonuniform, he knew that the direction of its total gravitational force was very nearly toward the earth's center. That was strong evidence that the distribution of mass was very symmetric, so that we can think of the earth as being made of layers, like an onion, with each layer having constant density throughout. (Today there is further evidence for symmetry based on measurements of how the vibrations from earthquakes and nuclear explosions travel through the earth.) He then considered the gravitational forces exerted by a single such thin shell, and proved the following theorem, known as the shell theorem:
Actually, Newton had sound reasons for treating the earth's mass as if it was concentrated at its center. First, although Newton no doubt suspected the earth's density was nonuniform, he knew that the direction of its total gravitational force was very nearly toward the earth's center. That was strong evidence that the distribution of mass was very symmetric, so that we can think of the earth as being made of layers, like an onion, with each layer having constant density throughout. (Today there is further evidence for symmetry based on measurements of how the vibrations from earthquakes and nuclear explosions travel through the earth.) He then considered the gravitational forces exerted by a single such thin shell, and proved the following theorem, known as the shell theorem:
If an object lies outside a thin, spherical shell of mass, then the vector sum of all the gravitational forces exerted by all the parts of the shell is the same as if the shell's mass had been concentrated at its center. If the object lies inside the shell, then all the gravitational forces cancel out exactly.
For terrestrial gravity, each shell acts as though its mass was at the center, so the result is the same as if the whole mass was there.
The second part of the shell theorem, about the gravitational forces canceling inside the shell, is a little surprising. Obviously the forces would all cancel out if you were at the exact center of a shell, but it's not at all obvious that they should still cancel out perfectly if you are inside the shell but off-center. The whole idea might seem academic, since we don't know of any hollow planets in our solar system that astronauts could hope to visit, but actually it's a useful result for understanding gravity within the earth, which is an important issue in geology. It doesn't matter that the earth is not actually hollow. In a mine shaft at a depth of, say, 2 km, we can use the shell theorem to tell us that the outermost 2 km of the earth has no net gravitational effect, and the gravitational force is the same as what would be produced if the remaining, deeper, parts of the earth were all concentrated at its center.
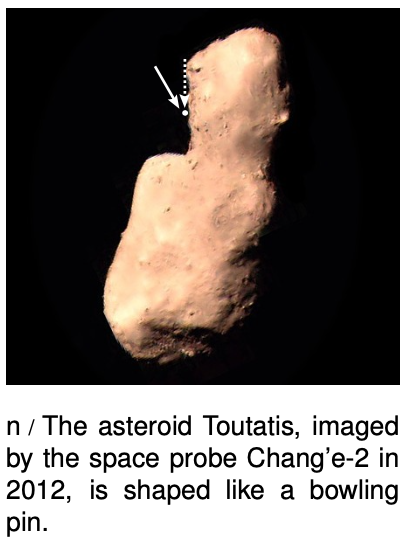 The shell theorem doesn't apply to things that aren't spherical. At the point marked with a dot in figure n, we might imagine that gravity was in the direction shown by the dashed arrow, pointing toward the asteroid's center of mass, so that the surface would be a vertical cliff almost a kilometer tall. In reality, calculations based on the assumption of uniform density show that the direction of the gravitational field is approximately as shown by the solid arrow, making the slope only about `60°`. This happens because gravity at this location is more strongly affected by the nearby “neck” than by the more distant “belly.” This slope is still believed to be too steep to keep dirt and rocks from sliding off (see problem 11, p. 233).
The shell theorem doesn't apply to things that aren't spherical. At the point marked with a dot in figure n, we might imagine that gravity was in the direction shown by the dashed arrow, pointing toward the asteroid's center of mass, so that the surface would be a vertical cliff almost a kilometer tall. In reality, calculations based on the assumption of uniform density show that the direction of the gravitational field is approximately as shown by the solid arrow, making the slope only about `60°`. This happens because gravity at this location is more strongly affected by the nearby “neck” than by the more distant “belly.” This slope is still believed to be too steep to keep dirt and rocks from sliding off (see problem 11, p. 233).
self-check:
Suppose you're at the bottom of a deep mineshaft, which means you're still quite far from the center of the earth. The shell theorem says that the shell of mass you've gone inside exerts zero total force on you. Discuss which parts of the shell are attracting you in which directions, and how strong these forces are. Explain why it's at least plausible that they cancel.
(answer in the back of the PDF version of the book)
Discussion Questions
A If you hold an apple, does the apple exert a gravitational force on the earth? Is it much weaker than the earth's gravitational force on the apple? Why doesn't the earth seem to accelerate upward when you drop the apple?
B When astronauts travel from the earth to the moon, how does the gravitational force on them change as they progress?
C How would the gravity in the first-floor lobby of a massive skyscraper compare with the gravity in an open field outside of the city?
D In a few billion years, the sun will start undergoing changes that will eventually result in its puffing up into a red giant star. (Near the beginning of this process, the earth's oceans will boil off, and by the end, the sun will probably swallow the earth completely.) As the sun's surface starts to get closer and closer to the earth, how will the earth's orbit be affected?
10.4 Vector addition of gravitational forces by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.