The Circle Calculator provides the area, circumference, radius and diameter equations employing many different length and area units 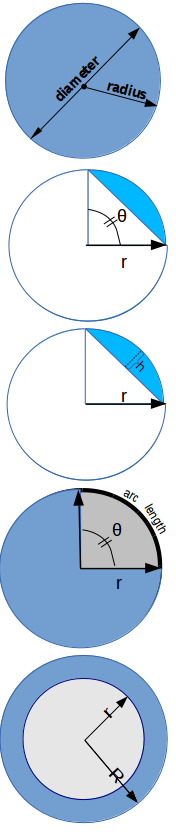 Circles and
Circles and
Circle segments as follows:
- Circle Area - This computes the area of a circle given the radius (A = π r2).
- Segment Area f(r,θ) - This computes the area of an arc segment of a circle given the radius (r) and angle (θ)
- Segment Area f(r,h) - This computes the area of an arc segment of a circle given radius (r) and the depth (h) into the circle.
- Sector Area f(r,θ)- This computes the area of a sector (pie slice) of a circle given the radius (r) and angle (θ).
- Area of Annulus- This computes the area of an annulus (ring) given the inner radius (r) and outer radius (R).
- Radius from Center to a Point - This computes the radius of a circle given the center point (h,k) and any other point (x,y) on the circle.
- Circumference - This computes the circumference of a circle given the radius (C = 2 π r).
- Arc Lengths - This computes the length of a chord segment (arc length) on a circle given the radius (r) and angle (?)
- Circle within a Triangle - This computes the radius of a circle inscribed within a triangle given the length of the three sides (a,b,c) of the triangle.
- Circle around a Triangle - This computes the radius of a circle that circumscribes a triangle given the length of the three sides (a,b,c) of the triangle.
- Radius from Circumference - This computes the radius of a circle given the circumference.
- Circumference from Area - This computes the circumference of a circle given the area.
- Radius from Area - This computes the radius of a circle given the area.
- Radius from Chord- This computes the radius of a circle based on the length of a chord and the cord's center height.
The Circle
A circle is a simple shape in Euclidean geometry. It is the set of all points in a plane that are at a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves so that its distance from a given point is constant. The distance between any of the points and the center is called the radius.
A circle is a simple closed curve which divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is the former and the latter is called a disk.
A circle may also be defined as a special ellipse in which the two foci are coincident and the eccentricity is 0, or the two-dimensional shape enclosing the most area per unit perimeter, using calculus of variations.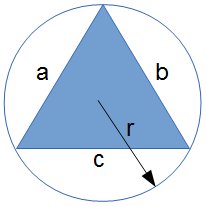 circle around triangle
circle around triangle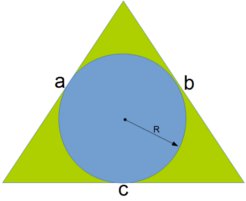 circle within triangle
circle within triangle  Radius of circle from cord length and height
Radius of circle from cord length and height
History
The word "circle" derives from the Greek (kirkos/kuklos), itself a metathesis of the Homeric Greek (krikos), meaning "hoop" or "ring". The origins of the words "circus" and "circuit" are closely related.
The circle has been known since before the beginning of recorded history. Natural circles would have been observed, such as the Moon, Sun, and a short plant stalk blowing in the wind on sand, which forms a circle shape in the sand. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy, and calculus.
Early science, particularly geometry and astrology and astronomy, was connected to the divine for most medieval scholars, and many believed that there was something intrinsically "divine" or "perfect" that could be found in circles.
Some highlights in the history of the circle are:
- 1700 BCE – The Rhind papyrus gives a method to find the area of a circular field. The result corresponds to 256/81 (3.16049...) as an approximate value of π
- 300 BCE – Book 3 of Euclid's Elements deals with the properties of circles.
- In Plato's Seventh Letter there is a detailed definition and explanation of the circle. Plato explains the perfect circle and how it is different from any drawing, words, definition or explanation.
- 1880 CE– Lindemann proves that ? is transcendental, effectively settling the millennia-old problem of squaring the circle.
References
- wikipedia - http://en.wikipedia.org/wiki/Circle